Energy of an Orbiting Satellite (AQA A Level Physics) : Revision Note
Energy of an Orbiting Satellite
An orbiting satellite follows a circular path around a planet
Just like an object moving in circular motion, it has both kinetic energy (KE) and gravitational potential energy (GPE) and its total energy is always constant
An orbiting satellite's total energy is calculated by:
Total energy = Kinetic energy + Gravitational potential energy
This means that the satellite's KE and GPE are also both constant in a particular orbit
If the orbital radius of a satellite decreases its KE increases and its GPE decreases
If the orbital radius of a satellite increases its KE decreases and its GPE increases
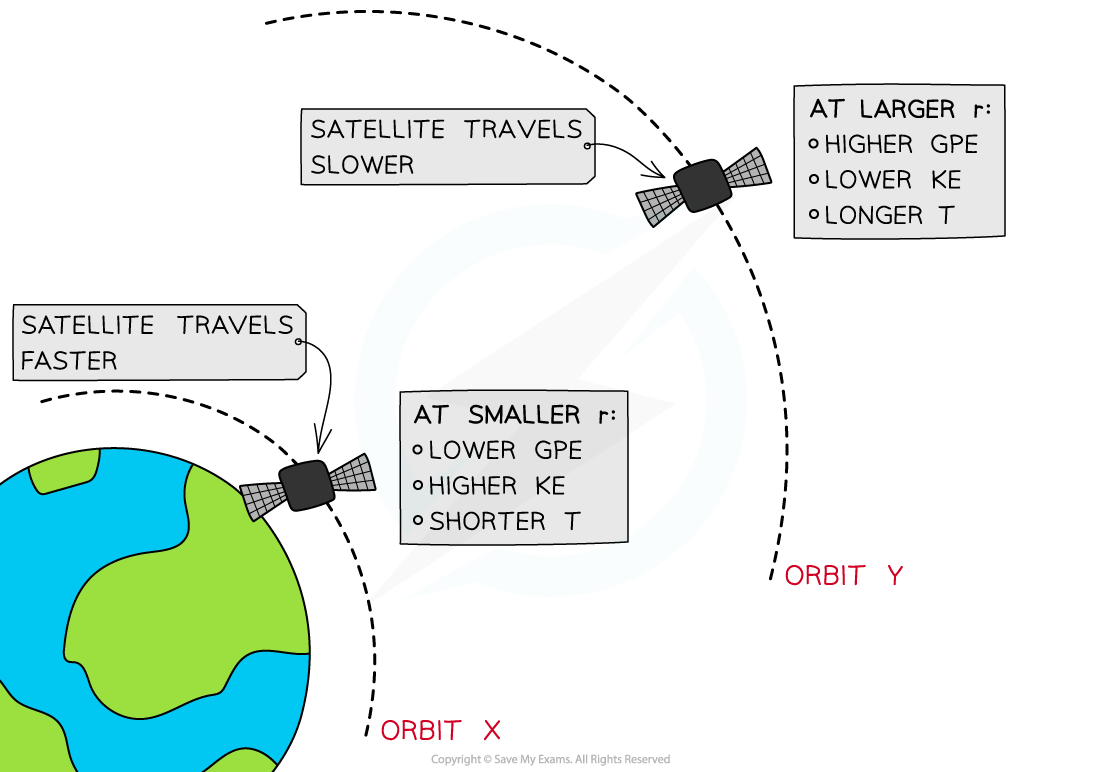
At orbit Y, the satellite has greater GPE and less KE than at at orbit X
A satellite is placed in two orbits, X and Y, around Earth
At orbit X, where the radius of orbit r is smaller, the satellite has a:
Larger gravitational force on it
Higher speed
Higher KE
Lower GPE
Shorter orbital time period, T
At orbit Y, where the radius of orbit r is larger, the satellite has a:
Smaller gravitational force on it
Smaller speed
Lower KE
Higher GPE
Longer orbital time period, T
Worked Example
Two satellites A and B, of equal mass, orbit a planet at radii R and 3R respectively. Which one of the following statements is incorrect?
A. A has more kinetic energy and less potential energy than B
B. A has a shorter time period and travels faster than B
C. B has less kinetic energy and more potential energy than A
D. B has a longer time period and travels faster than A
Answer: D
Since B is at a larger orbital radius (3R instead of R) it has a longer time period since T2 ∝ R3 for an orbiting satellite
However, satellite B will travel much slower than A
Its larger orbital radius means the force of gravity will be much lower for B than for A
Examiner Tips and Tricks
If you can't remember which way around the kinetic and potential energy increases and decreases, think about the velocity of a satellite at different orbits. When it is orbiting close to a planet, it experiences a larger gravitational pull and therefore orbits faster. Since the kinetic energy is proportional to v2, it, therefore, has higher kinetic energy closer to the planet. To keep the total energy constant, the potential energy must decrease too.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
