Work Done on a Mass (AQA A Level Physics) : Revision Note
Work Done on a Mass
When a mass is moved against the force of gravity, work is done
The work done in moving a mass m is given by:
∆W = m∆V
Where:
∆W = change in work done (J)
m = mass (kg)
∆V = change in gravitational potential (J kg-1)
This change in work done is equal to the change in gravitational potential energy (G.P.E)
When V = 0, then the G.P.E = 0
The change in G.P.E, or work done, for an object of mass m at a distance r1 from the centre of a larger mass M, to a distance of r2 further away can be written as:

Where:
M = mass that is producing the gravitational field (eg. a planet) (kg)
m = mass that is moving in the gravitational field (eg. a satellite) (kg)
r1 = first distance of m from the centre of M (m)
r2 = second distance of m from the centre of M (m)
Work is done when an object in a planet's gravitational field moves against the gravitational field lines ie. away from the planet
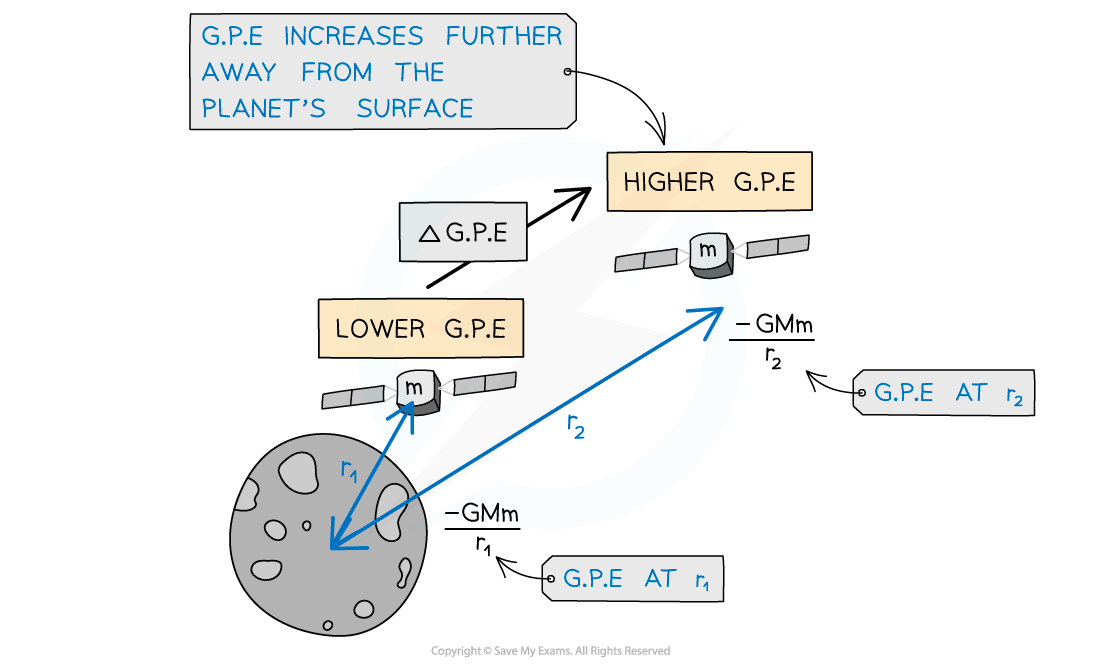
Gravitational potential energy increases as a satellite leaves the surface of the Moon
Maths Tip
Multiplying two negative numbers equals a positive number, for example:
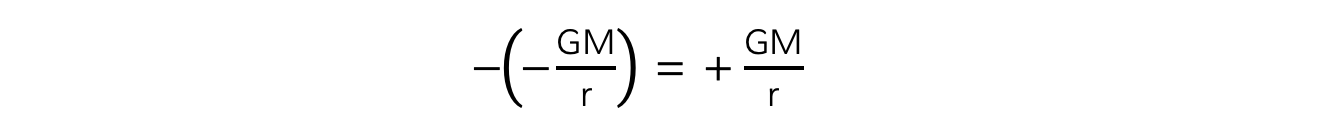
Worked Example
A spacecraft of mass 300 kg leaves the surface of Mars to an altitude of 700 km. Calculate the work done by the spacecraft. Radius of Mars = 3400 km
Mass of Mars = 6.40 × 1023 kg
Answer:
Step 1: Write down the work done (or change in G.P.E) equation
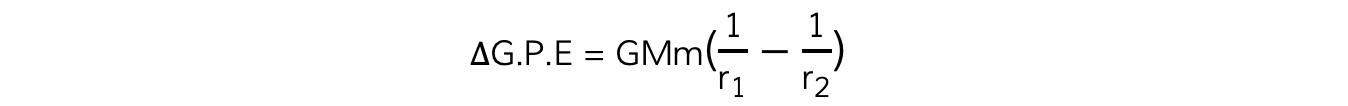
Step 2: Determine values for r1 and r2
r1 is the radius of Mars = 3400 km = 3400 × 103 m
r2 is the radius + altitude = 3400 + 700 = 4100 km = 4100 × 103 m
Step 3: Substitute in values
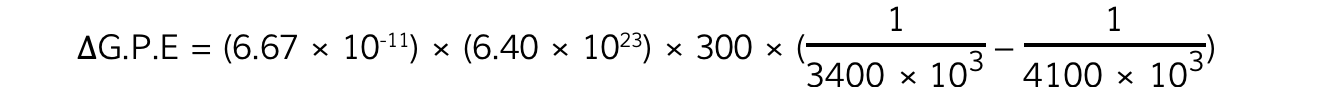
ΔG.P.E = 643.076 × 106 = 640 MJ (2 s.f.)
Examiner Tips and Tricks
Make sure to not confuse the ΔG.P.E equation with
ΔG.P.E = mgΔh
The above equation is only relevant for an object lifted in a uniform gravitational field (close to the Earth’s surface).The new equation for G.P.E will not include g, because this varies for different planets and is no longer a constant (decreases by 1/r2) outside the surface of a planet.
Gravitational Equipotential Surfaces
Equipotential lines (2D) and surfaces (3D) join together points that have the same gravitational potential
These are always:
Perpendicular to the gravitational field lines in both radial and uniform fields
Represented by dotted lines (unlike field lines, which are solid lines with arrows)
In a radial field (e.g. a planet), the equipotential lines:
Are concentric circles around the planet
Can become further apart as they move further away from the planet
In a radial field equipotential lines can become further apart as they move further away from the planet because
potential decreases with distance away
the gravitational field gets weaker with distance away
a greater distance needs to be moved to obtain the same change in potential, ΔV
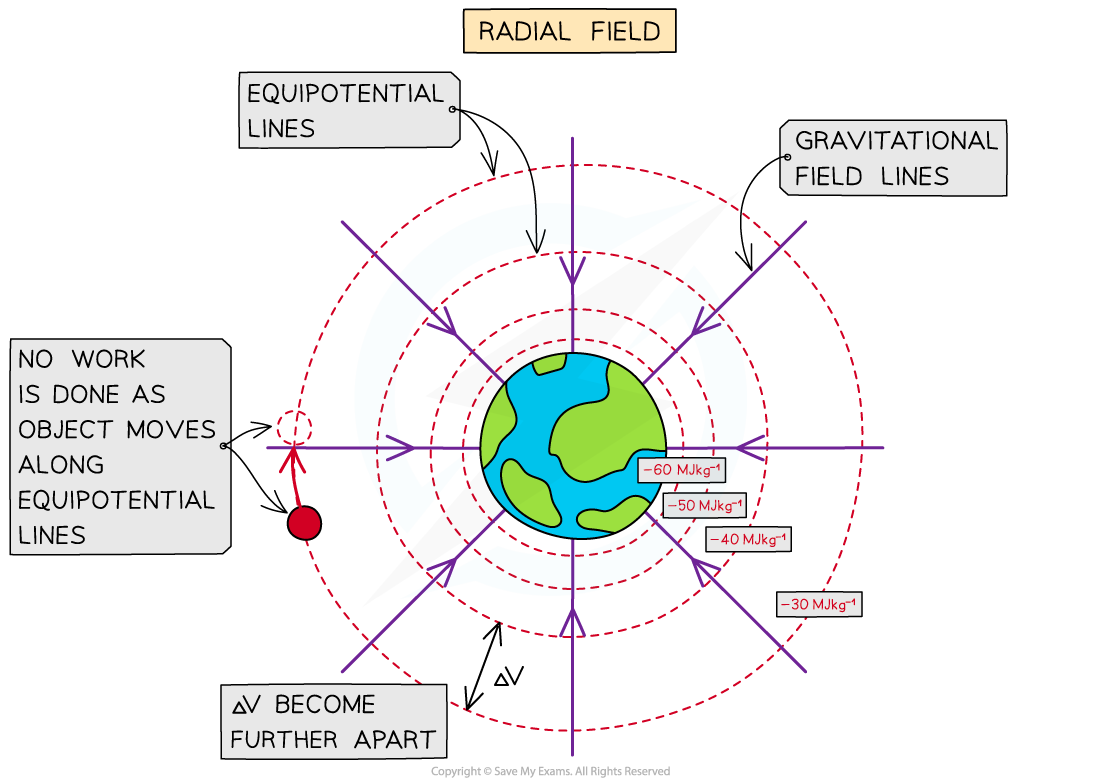
In a radial field equipotential lines are concentric circles around the object
In a uniform field (eg. near the Earth's surface), the equipotential lines are:
Horizontal straight lines
Parallel
Equally spaced
No work is done when moving along an equipotential line or surface, only between equipotential lines or surfaces
This means that an object travelling along an equipotential doesn't lose or gain energy and ΔV = 0
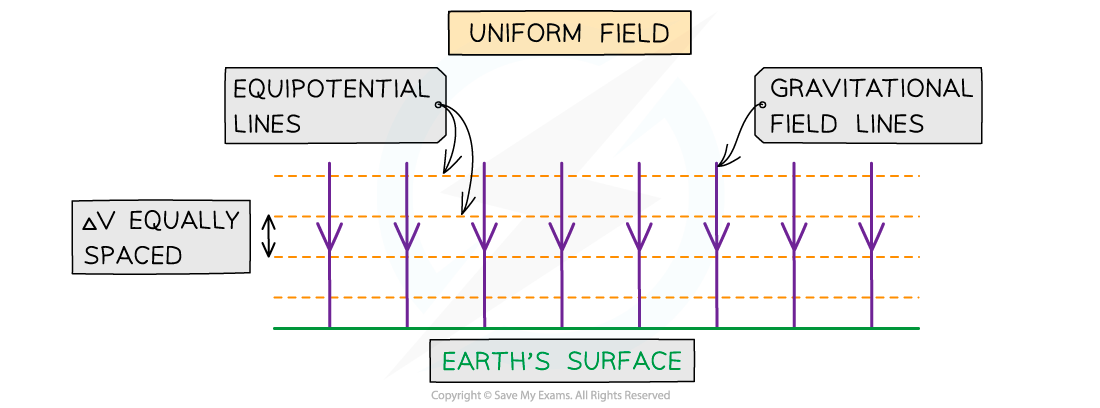
Gravitational equipotential lines in a uniform gravitational field are equally spaced
Examiner Tips and Tricks
Remember equipotential lines should not have arrows on them like gravitational field lines do, since they have no particular direction and are not vectors. Make sure to draw any straight lines with a ruler or a straight edge.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
