Graphical Representation of Gravitational Potential (AQA A Level Physics)

• Gravitational field strength, g and the gravitational potential, V can be graphically represented against the distance from the centre of a planet, r
• g, V and r are related by the equation:

• Where:
  • g = gravitational field strength (N kg^-1)
  • ΔV = change in gravitational potential (J kg^-1)
  • Δr = distance from the centre of a point mass (m)

• The graph of V against r for a planet is:

The gravitational potential and distance graphs follows a -1/r relation

• The key features of this graph are:
  • The values for V are all negative 
  • (because the graph is drawn below the horizontal r axis)
  • As r increases, V against r follows a -1/r relation
  • The gradient of the graph at any particular point is the value of g at that point, 
  • The graph has a shallow increase as r increases

• To calculate g, draw a tangent to the graph at that point and calculate the gradient of the tangent
• This is a graphical representation of the equation:

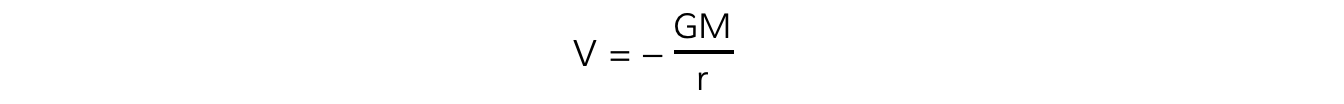
where G and M are constant

• The graph of g against r for a planet is:

The gravitational field strength and distance graph follows a 1/r2 relation

• The key features of this graph are:
  • The values for g are all positive
  • As r increases, g against r follows a 1/r² relation (inverse square law)
  • The area under this graph is the change in gravitational potential ΔV
  • The graph has a steep decline as r increases

 

• The area under the graph can be estimated by counting squares, if it is plotted on squared paper, or by splitting it into trapeziums and summing the area of each trapezium
• The inverse square law relation means that as the distance r doubles, g decreases by a factor of 4
• This is a graphical representation of the equation:

where G and M are constant

• Graph increases from a large negative value for V at the surface of A as distance increases
• Up to a value close to, but below 0 near the surface of planet B
• The graph then falls near the surface of planet B
• From a point much closer to planet B than A