Calculating Gravitational Potential (AQA A Level Physics): Revision Note
Exam code: 7408
Calculating Gravitational Potential
The equation for gravitational potential V is defined by the mass M and distance r:
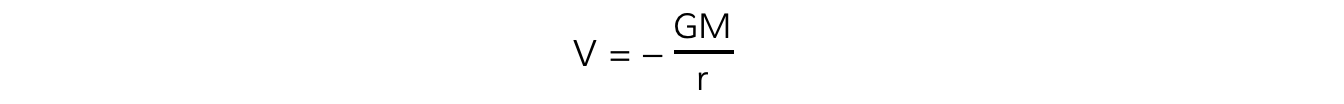
Where:
V = gravitational potential (J kg-1)
G = Newton’s gravitational constant
M = mass of the body producing the gravitational field (kg)
r = distance from the centre of the mass to the point mass (m)
The gravitational potential always is negative near an isolated mass, such as a planet, because:
The potential when r is at infinity (∞) is defined as 0
Work must be done to move a mass away from a planet (V becomes less negative)
It is also a scalar quantity, unlike the gravitational field strength which is a vector quantity
Gravitational forces are always attractive, this means as r decreases, positive work is done by the mass when moving from infinity to that point
When a mass is closer to a planet, its gravitational potential becomes smaller (more negative)
As a mass moves away from a planet, its gravitational potential becomes larger (less negative) until it reaches 0 at infinity
This means when the distance (r) becomes very large, the gravitational force tends rapidly towards 0 at a point further away from a planet
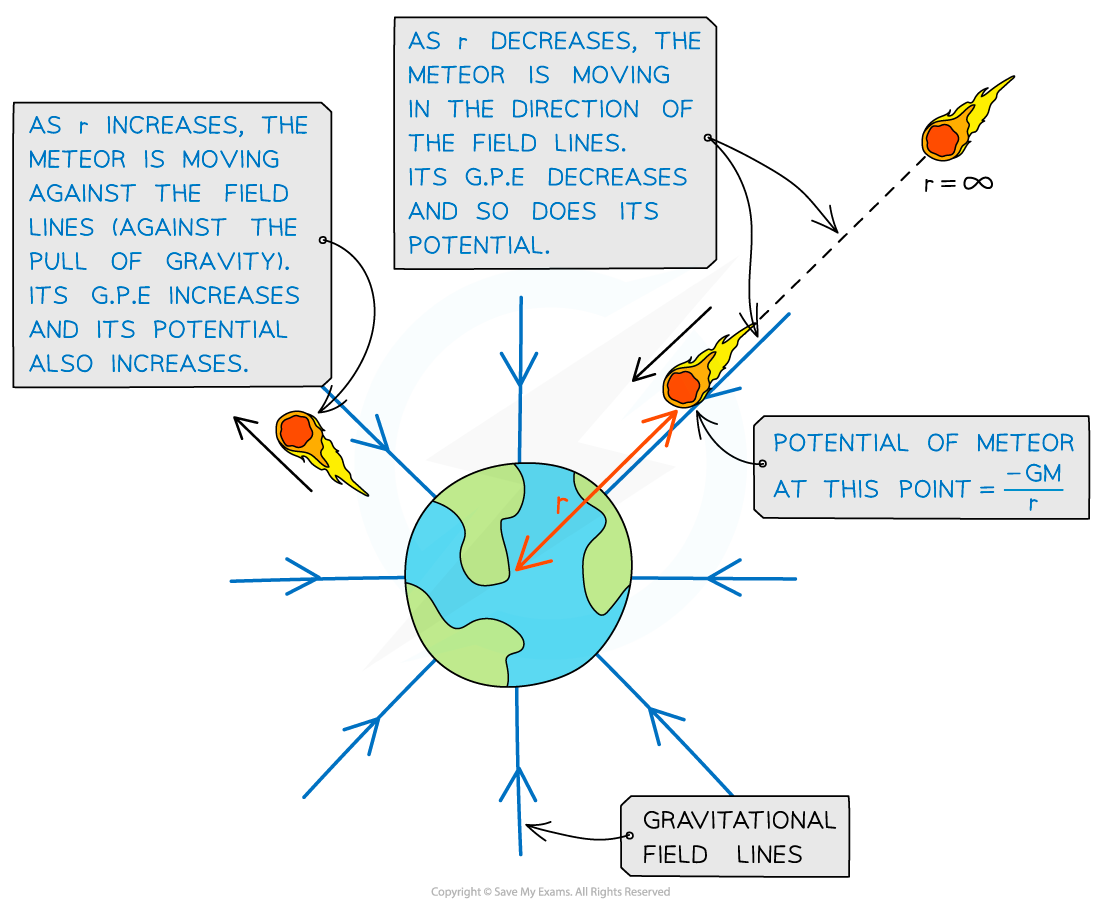
Gravitational potential increases and decreases depending on whether the object is travelling towards or against the field lines from infinity
Worked Example
A planet has a diameter of 7600 km and a mass of 3.5 × 1023 kg. A rock of mass 528 kg accelerates towards the planet from infinity. At a distance of 400 km above the planet's surface, calculate the gravitational potential of the rock.
Answer:
Step 1: Write the gravitational potential equation
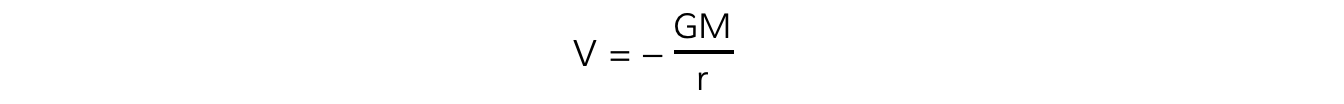
Step 2: Determine the value of r
r is the distance from the centre of the planet
Radius of the planet = planet diameter ÷ 2 = 7600 ÷ 2 = 3800 km
r = 3800 + 400 = 4200 km = 4.2 × 106 m
Step 3: Substitute in values
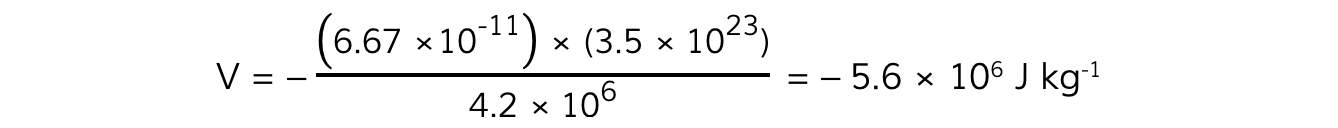
Examiner Tips and Tricks
Remember to keep the negative sign in your solution for the gravitational potential at a point. However, if you’re asked for the ‘change in’ gravitational potential, no negative sign needs to be included since you are finding a difference in values and just the magnitude is normally required. Remember to also calculate r as the distance from the centre of the planet, and not just the distance above the planet's surface

Unlock more, it's free!
Did this page help you?