Gravitational Field Strength in a Radial Field (AQA A Level Physics): Revision Note
Exam code: 7408
Gravitational Field Strength in a Radial Field
The gravitational field strength at a point describes how strong or weak a gravitational field is at that point
The equation for gravitational field strength due to a point mass is:
Where:
g = gravitational field strength (N kg-1)
G = Newton’s gravitational constant
M = mass of the body producing the gravitational field (kg)
r = distance between point source (mass, m) and position in field (m)
Gravitational field strength, g, is a vector quantity
The direction of g is always towards the centre of the body creating the gravitational field
This is the same direction as the gravitational field lines
On the Earth’s surface, g has a constant value of 9.81 N kg-1
However, outside the Earth’s surface, g is not constant
g decreases as r increases by a factor of 1/r2
This is an inverse square law relationship with distance
When g is plotted against the distance from the centre of a planet, r has two parts:
When r < R, the radius of the planet, g is directly proportional to r
When r > R, g is inversely proportional to r2 (this is an ‘L’ shaped curve and shows that g decreases rapidly with increasing distance r)
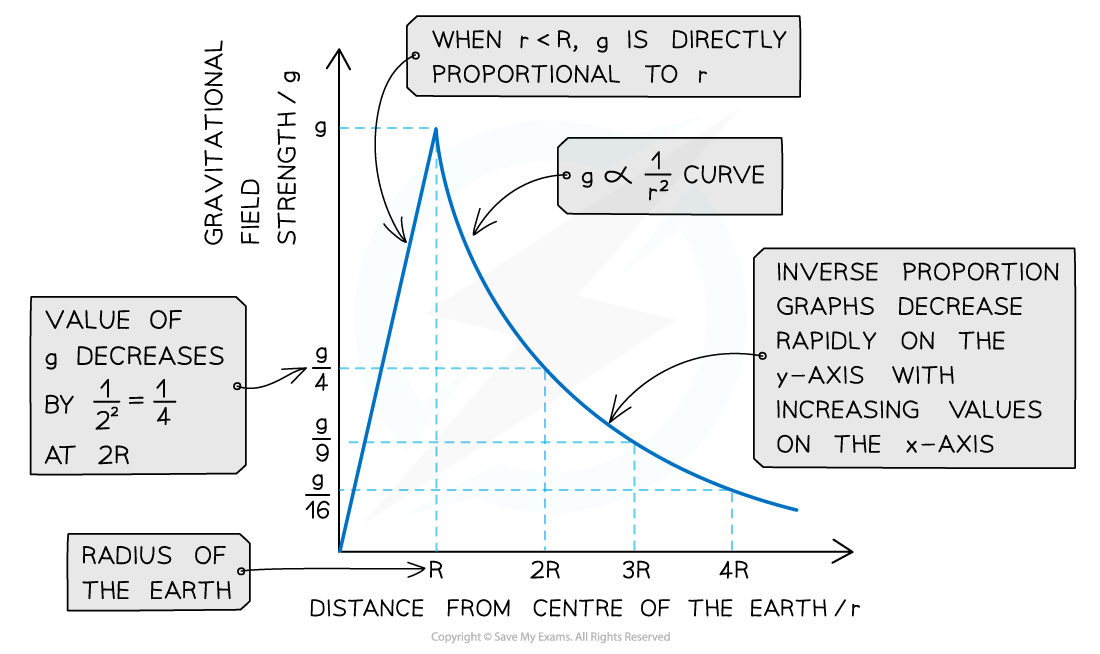

Graph showing how gravitational field strength varies at greater distance from the Earth’s surface
Sometimes, g is referred to as the ‘acceleration due to gravity’ with units of m s-2
Any object that falls freely in a uniform gravitational field on Earth has an acceleration of 9.81 m s-2
Worked Example
The mean density of the Moon is 3/5 times the mean density of the Earth. The gravitational field strength on the Moon is 1/6 of the value on Earth.
Determine the ratio of the Moon's radius rM and the Earth's radius rE.
Answer:
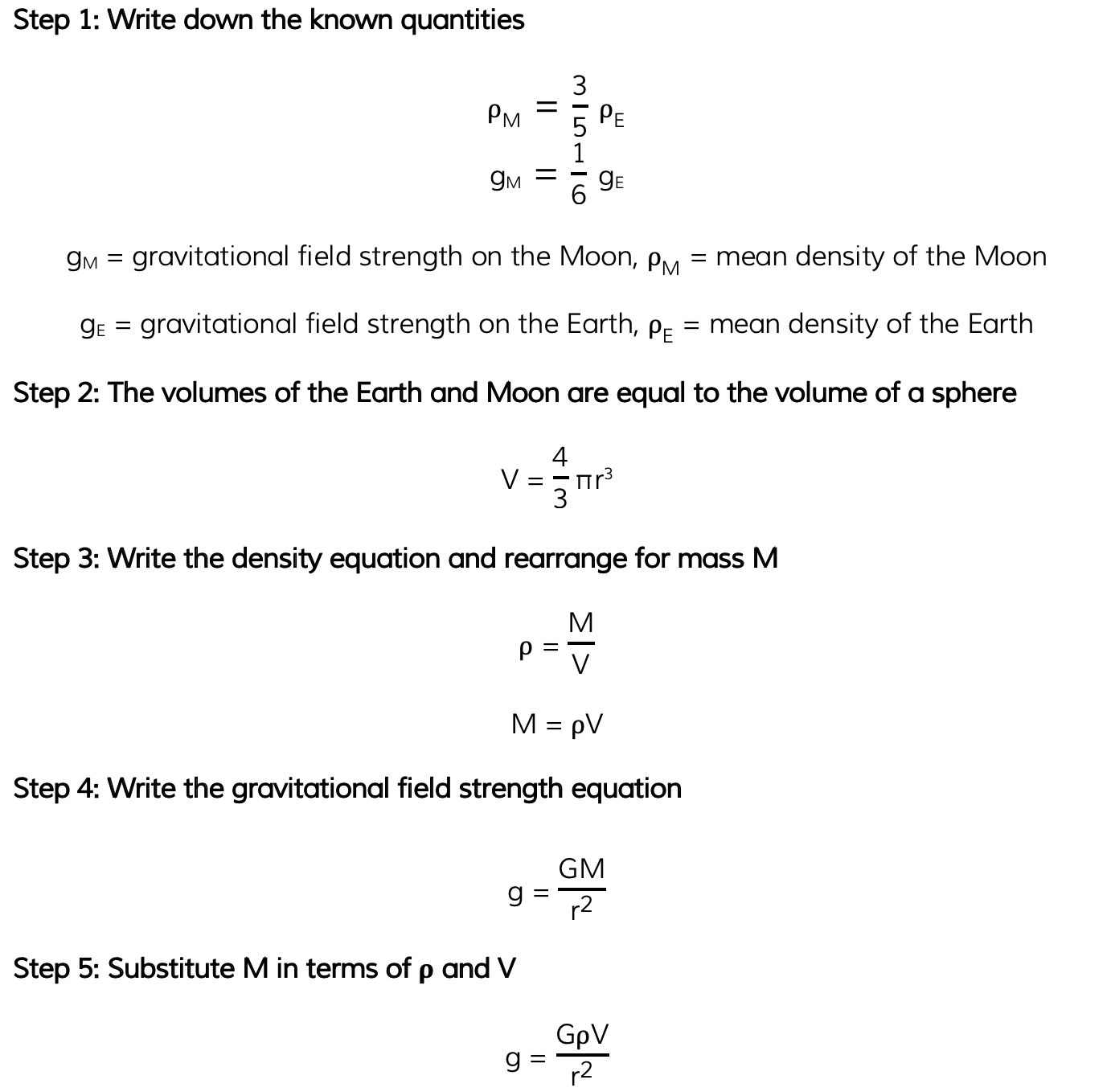
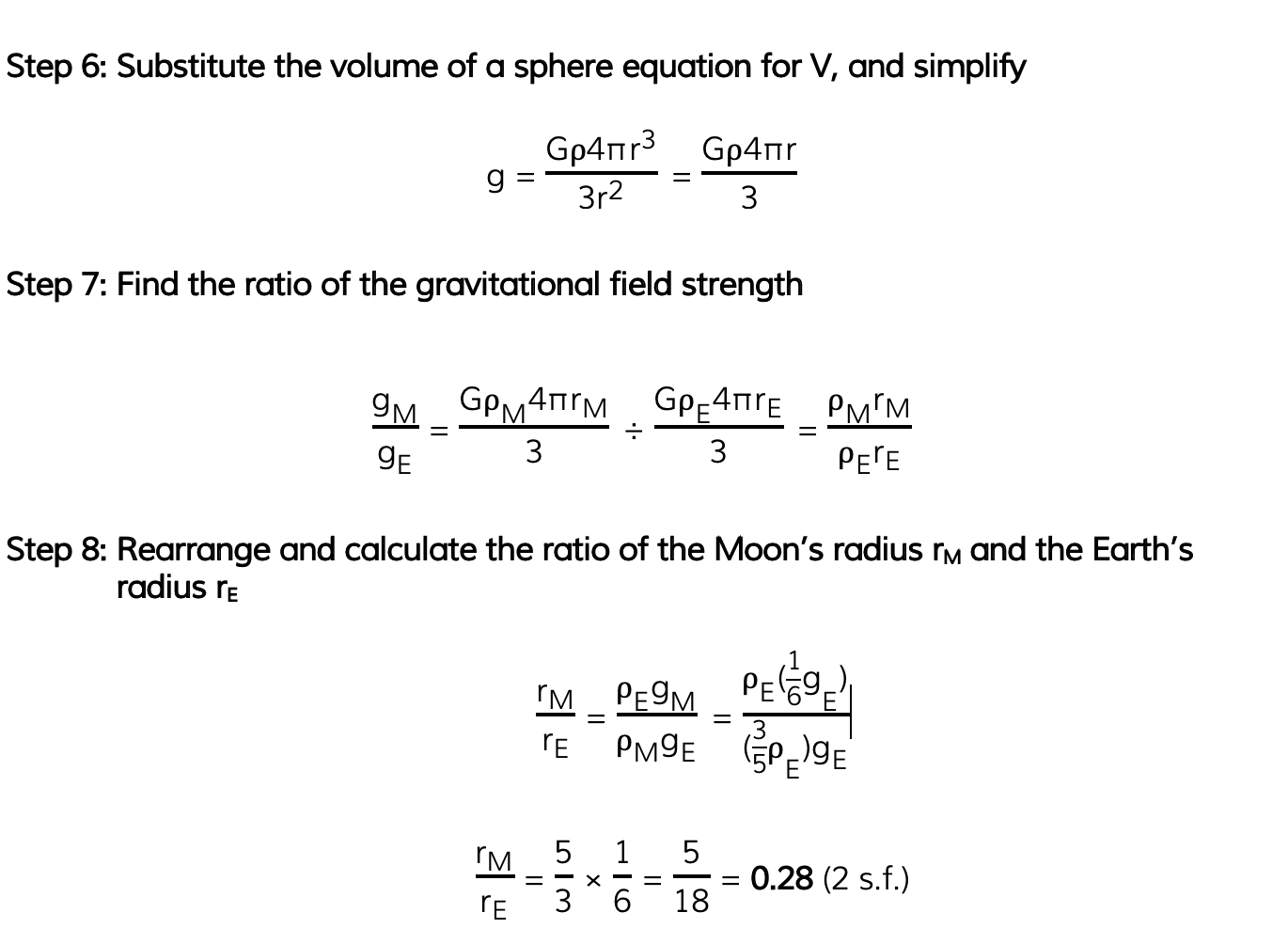
Examiner Tips and Tricks
Remember that r is always taken from the centre of mass of the object creating the gravitational field.
Also, make sure you're comfortable with drawing the inverse square law graph of g against r, since this is a common exam question

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?