Charge & Discharge Equations (AQA A Level Physics)
Revision Note
Capacitor Discharge Equation
The time constant is used in the exponential decay equations for the current, charge or potential difference (p.d) for a capacitor discharging through a resistor
These can be used to determine the amount of current, charge or p.d left after a certain amount of time for a discharging capacitor
This exponential decay means that no matter how much charge is initially on the plates, the amount of time it takes for that charge to halve is the same
The exponential decay of current on a discharging capacitor is defined by the equation:
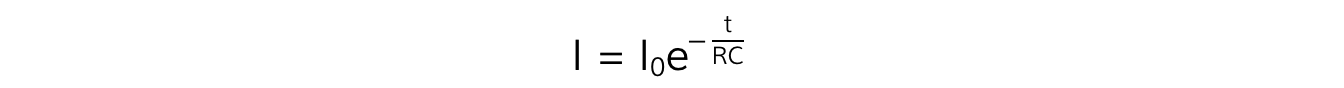
Where:
I = current (A)
I0 = initial current before discharge (A)
e = the exponential function
t = time (s)
RC = resistance (Ω) × capacitance (F) = the time constant τ (s)
This equation shows that the smaller the time constant τ, the quicker the exponential decay of the current when discharging
Also, how big the initial current is affects the rate of discharge
If I0 is large, the capacitor will take longer to discharge
Note: during capacitor discharge, I0 is always larger than I, as the current I will always be decreasing
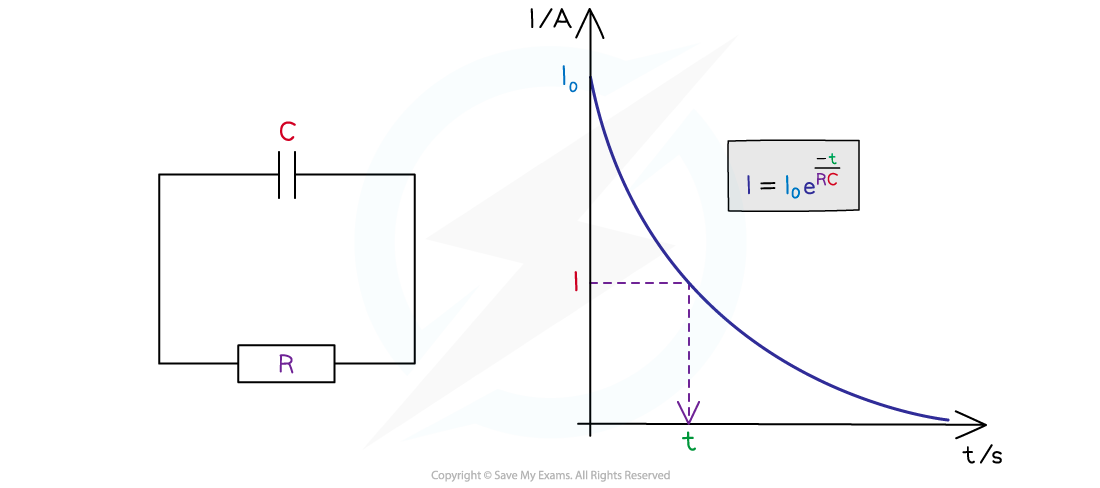
Values of the capacitor discharge equation on a graph and circuit
The current at any time is directly proportional to the p.d across the capacitor and the charge across the parallel plates
Therefore, this equation also describes the charge on the capacitor after a certain amount of time:
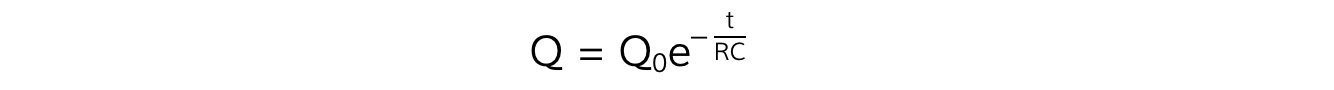
Where:
Q = charge on the capacitor plates (C)
Q0 = initial charge on the capacitor plates (C)
As well as the p.d after a certain amount of time:

Where:
V = p.d across the capacitor (C)
V0 = initial p.d across the capacitor (C)
The Exponential Function e
The symbol e represents the exponential constant, a number which is approximately equal to e = 2.718...
On a calculator, it is shown by the button ex
The inverse function of ex is ln(y), known as the natural logarithmic function
This is because, if ex = y, then x = ln (y)
The 0.37 in the definition of the time constant arises as a result of the exponential constant, the true definition is:


Worked Example
The initial current through a circuit with a capacitor of 620 µF is 0.6 A.The capacitor is connected across the terminals of a 450 Ω resistor.Calculate the time taken for the current to fall to 0.4 A.
Answer:

Examiner Tips and Tricks
The equation for Q will be given on the data sheet, however you will be expected to remember that it is similar for I and V.
Capacitor Charge Equation
When a capacitor is charging, the way the charge Q and potential difference V increases stills shows exponential decay
Over time, they continue to increase but at a slower rate
This means the equation for Q for a charging capacitor is:
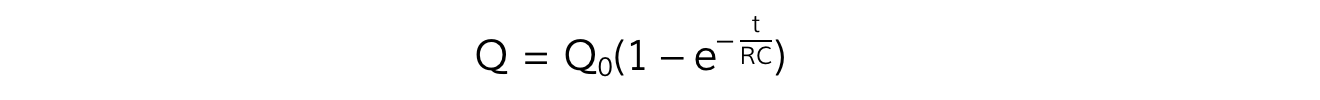
Where:
Q = charge on the capacitor plates (C)
Q0 = maximum charge stored on capacitor when fully charged (C)
e = the exponential function
t = time (s)
RC = resistance (Ω) × capacitance (F) = the time constant τ (s)
Similarly, for V:
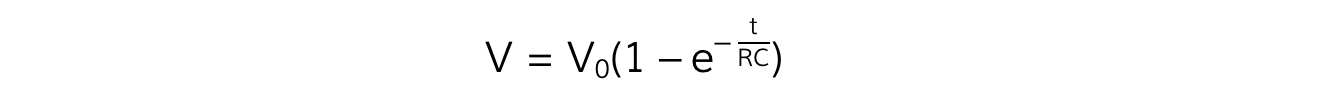
Where:
V = p.d across the capacitor (V)
V0 = maximum potential difference across the capacitor when fully charged (V)
The charging equation for the current I is the same as its discharging equation since the current still decreases exponentially
The key difference with the charging equations is that Q0 and V0 are now the final (or maximum) values of Q and V that will be on the plates, rather than the initial values
Worked Example
A capacitor is to be charged to a maximum potential difference of 12 V between its plate. Calculate how long it takes to reach a potential difference 10 V given that it has a time constant of 0.5 s.
Answer:
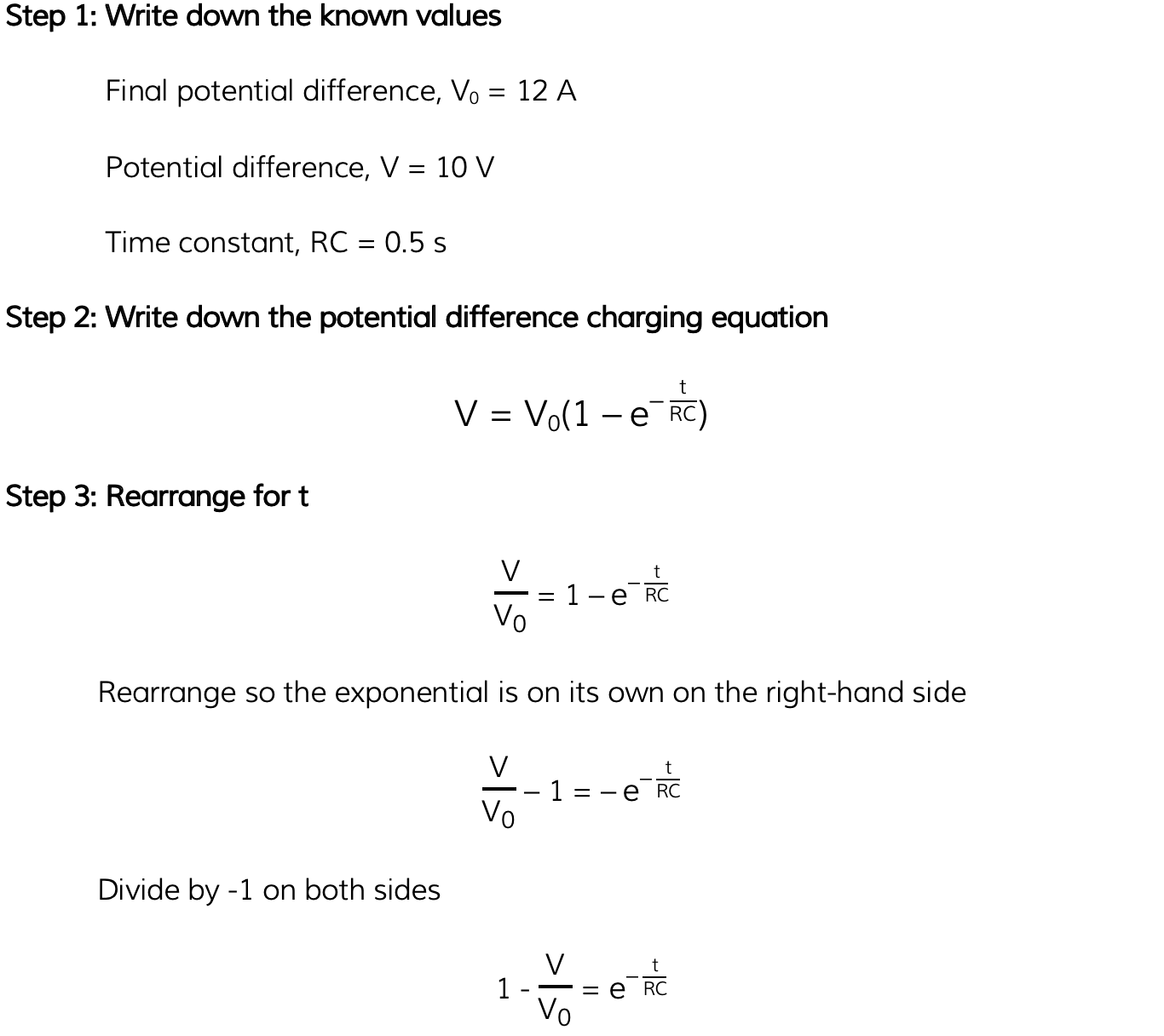
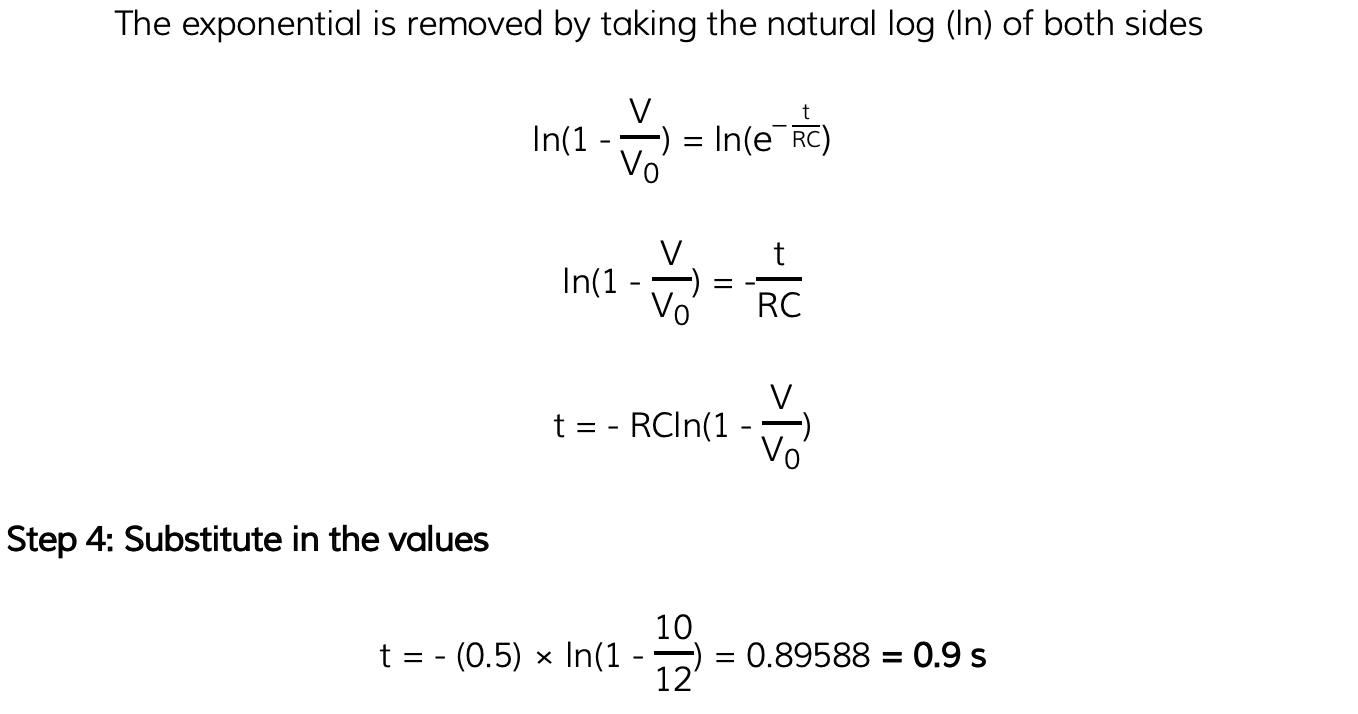
Examiner Tips and Tricks
Make sure you’re confident in rearranging equations with natural logs (ln) and the exponential function (e) for both charging and discharging equations. To refresh your knowledge of this, have a look at the AS Maths revision notes on Exponentials & Logarithms.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
