Avogadro, Molar Gas & Boltzmann Constant (AQA A Level Physics)

Avogadro's Constant

• The atomic mass unit (u) is approximately the mass of a proton or neutron = 1.66 × 10^-27 kg
• This means that an atom or molecule has a mass approximately equal to the number of protons and neutrons it contains
• A carbon-12 atom has a mass of:

12 u = 12 × 1.66 × 10^-27 = 1.99 × 10^-26 kg

• The exact number for a mole is defined as the number of molecules in exactly 12 g of carbon:

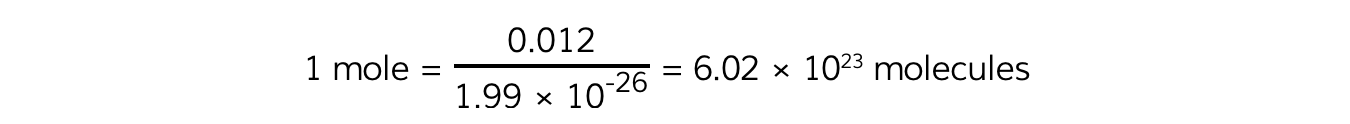
• Avogadro’s constant (N_A) is defined as:

 The number of atoms of carbon-12 in 12 g of carbon-12; equal to 6.02 × 10²³ mol^-1

• For example, 1 mole of sodium (Na) contains 6.02 × 10²³ atoms of sodium
• The number of atoms (or molecules) can be determined if the number of moles is known by multiplying by N_A, for example:

2.0 mol of helium contains:  2.0 × N_A = 2.0 × 6.02 × 10²³ = 1.20 × 10²⁴ atoms

Moles and Atomic Mass

• One mole of any element is equal to the relative atomic mass of that element in grams
  • For example, helium has an atomic mass of 4, meaning 1 mole of helium has a mass of 4 g

• If the substance is a compound, add up the relative atomic masses, for example, water (H₂O) is made up of
  • 2 hydrogen atoms (each with an atomic mass of 1) and 1 oxygen atom (atomic mass of 16)
  • So, 1 mole of water would have a mass of (2 × 1) + 16 = 18 g

Molar Mass

• The molar mass of a substance is the mass, in grams, in one mole
  • Its unit is g mol^-1

• The number of moles from this can be calculated using the equation:

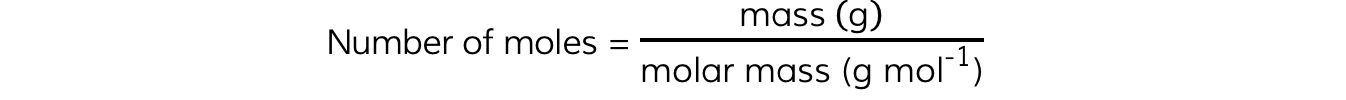
Boltzmann & The Molar Gas Constant

• The Boltzmann constant k is used in the ideal gas equation and is defined by the equation:

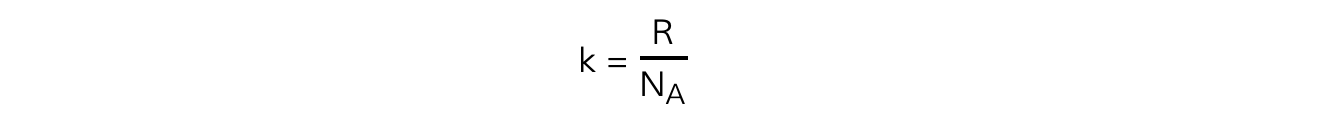
• Where:
  • R = molar gas constant
  • N_A = Avogadro’s constant

• Boltzmann’s constant, therefore, has a value of:

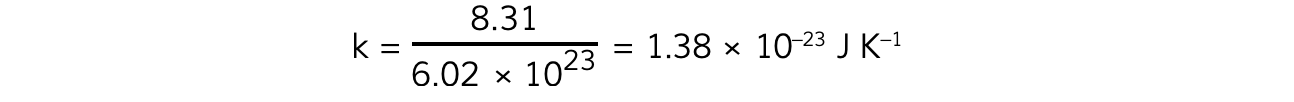
• The Boltzmann constant relates the properties of microscopic particles (e.g. kinetic energy of gas molecules) to their macroscopic properties (e.g. temperature)
  • This is why the units are J K^-1

• Its value is very small because the increase in kinetic energy of a molecule is very small for every incremental increase in temperature

Step 1: Calculate the mass of 1 mole of magnesium

      One mole of any element is equal to the relative atomic mass of that

      element in grams

1 mole = 24 g of magnesium

Step 2: Calculate the amount of moles in 6 g

Step 3: Convert the moles to number of atoms

1 mole = 6.02 × 10²³ atoms

0.25 moles = 0.25 × 6.02 × 10²³ = 1.51 × 10²³  atoms