Gas Laws (AQA A Level Physics)

• The ideal gas laws are the experimental relationships between pressure (P), volume (V) and temperature (T) of an ideal gas
• You need to be able to explain the following three ideal gas laws:
  • Boyles Law
  • Charles's Law
  • Pressure Law
• The mass and the number of molecules of the gas is assumed to be constant for all of these

Boyle’s Law

• If the temperature T of an ideal gas is constant, then Boyle’s Law is given by:

• This means the pressure is inversely proportional to the volume of a gas
• The relationship between the pressure and volume for a fixed mass of gas at constant temperature can also be written as:

P₁V₁ = P₂V₂

• Where:
  • P₁ = initial pressure (Pa)
  • P₂ = final pressure (Pa)
  • V₁ = initial volume (m³)
  • V₂ = final volume (m³)

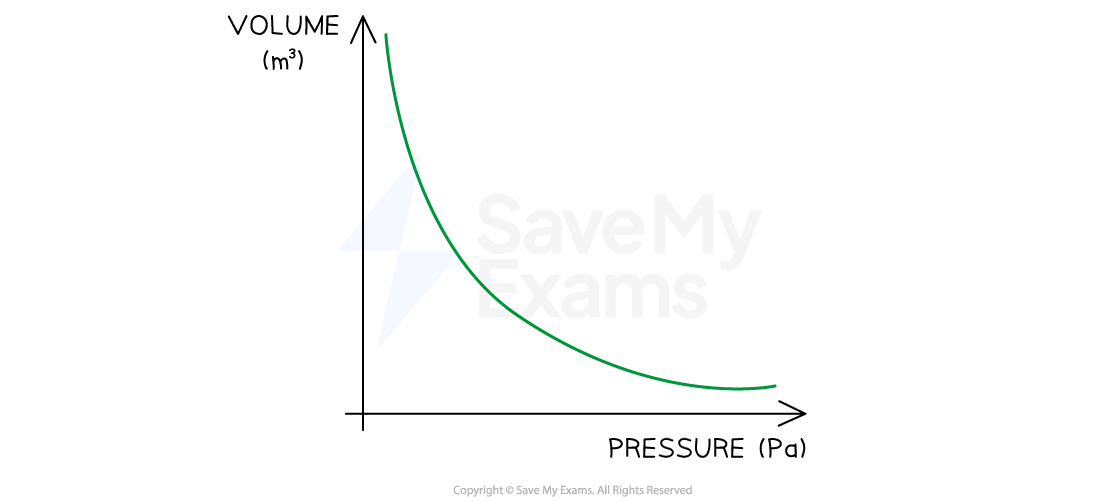
Boyle's Law graph representing pressure inversely proportional to volume

• If the temperature is higher but still constant, then the graph has the same shape but is shifted further above the origin

Charles's Law

• If the pressure P of an ideal gas is constant, then Charles’s law is given by:

V ∝ T

• This means the volume is directly proportional to the temperature of a gas
• The relationship between the volume and thermodynamic temperature for a fixed mass of gas at constant pressure can also be written as:

• Where:
  • V₁ = initial volume (m³)
  • V₂ = final volume (m³)
  • T₁ = initial temperature (K)
  • T₂ = final temperature (K)

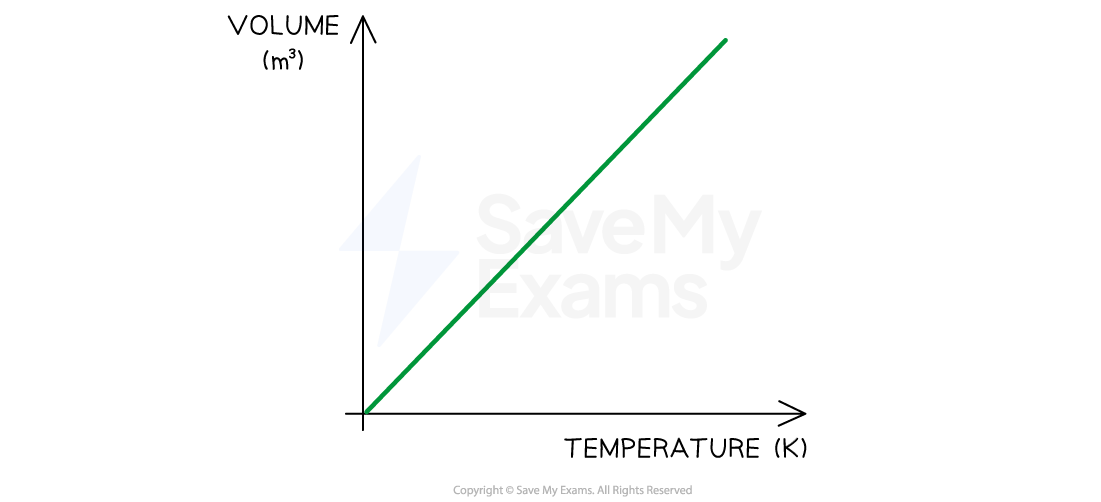
Charles's Law graph representing temperature (in K) directly proportional to the volume

• A straight line through the origin shows direct proportionality

Pressure Law

• If the volume V of an ideal gas is constant, the Pressure law is given by:

P ∝ T

• This means the pressure is proportional to the temperature
• The relationship between the pressure and thermodynamic temperature for a fixed mass of gas at constant volume can also be written as:

• Where:
  • P₁ = initial pressure (Pa)
  • P₂ = final pressure (Pa)
  • T₁ = initial temperature (K)
  • T₂ = final temperature (K)

Pressure Law graph representing temperature (in K) directly proportional to the volume

• A straight line through the origin shows direct proportionality between pressure and temperature in kelvin

• An ideal gas is one that obeys the relation:

pV ∝ T

• Where:
  • p = pressure of the gas (Pa)
  • V = volume of the gas (m³)
  • T = thermodynamic temperature (K)

• The molecules in a gas move around randomly at high speeds, colliding with surfaces and exerting pressure upon them

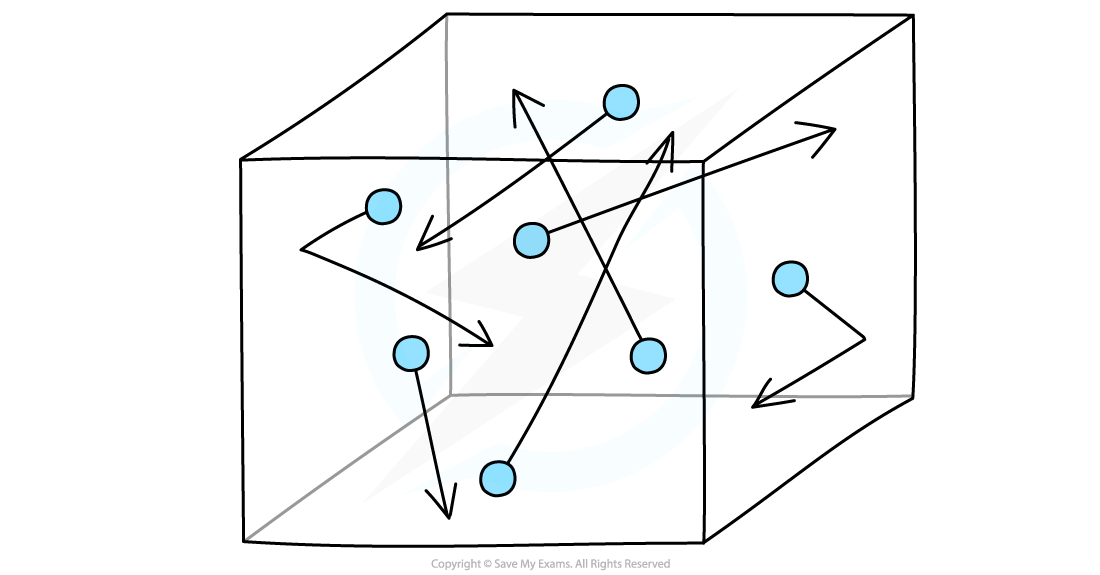
Gas molecules move about randomly at high speeds

• Imagine molecules of gas free to move around in a box
• The temperature of a gas is related to the average speed of the molecules:
  • The hotter the gas, the faster the molecules move
  • Hence the molecules collide with the surface of the walls more frequently

• Since force is the rate of change of momentum:
  • Each collision applies a force across the surface area of the walls
  • The faster the molecules hit the walls, the greater the force on them

• Since pressure is the force per unit area
  • Higher temperature leads to higher pressure

• If the volume V of the box decreases, and the temperature T stays constant:
  • There will be a smaller surface area of the walls and hence more collisions
  • This also creates more pressure

• Since this equates to a greater force per unit area, pressure in an ideal gas is therefore defined by:

The frequency of collisions of the gas molecules per unit area of a container

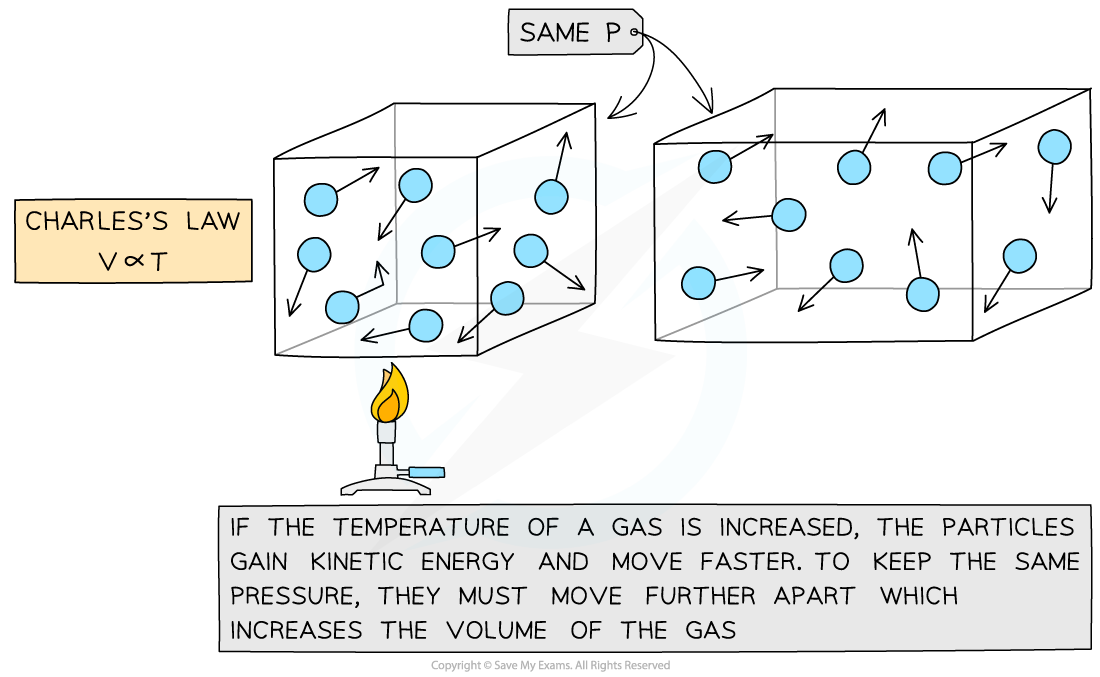
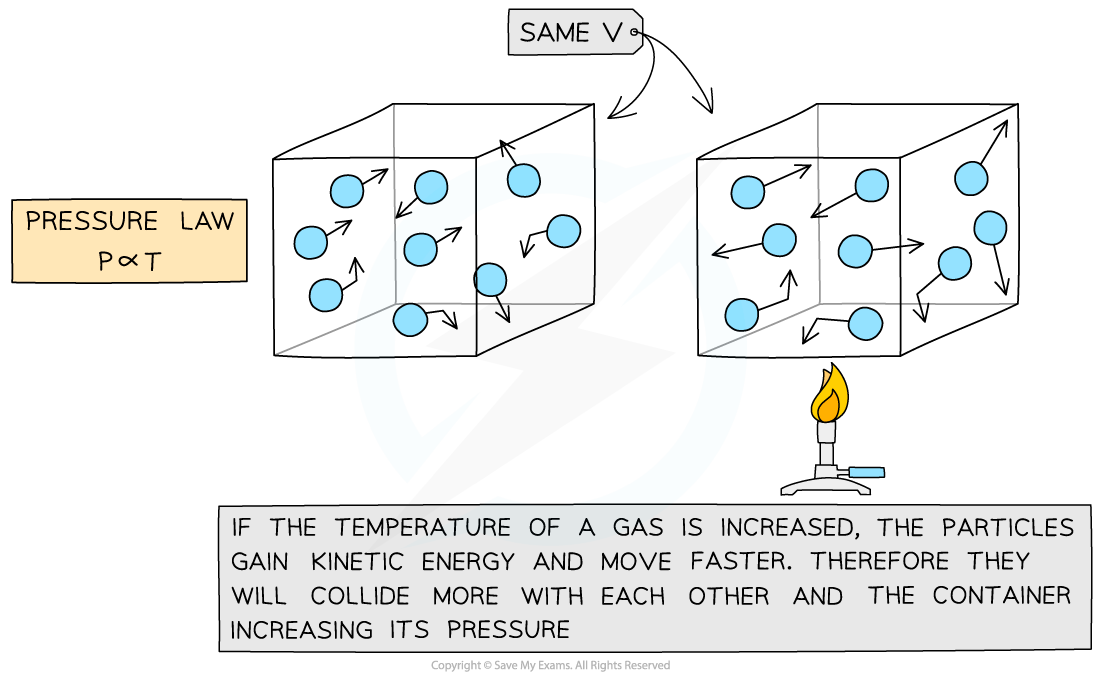
Molecular model of the three ideal gas laws

Step 1: Ideal gas relation between pressure, volume and temperature

pV ∝ T

Step 2: Write the equation in full

pV = kT

• • Where k = the constant of proportionality

Step 3: Rearrange for the constant of proportionality

Step 4: Convert temperature T into Kelvin

θ °C + 273.15 = T K

30 °C + 273.15 = 303.15 K

Step 5: Substitute in known value into constant of proportionality equation

Step 6: Rearrange ideal gas relation equation for pressure

Step 7: Substitute in new values

k = 9.203...

V stays the same = 4.5 × 10^-3 m³

T = 40 °C = 40 + 273.15 = 313.15 K