Latent Heat Capacity (AQA A Level Physics)

Revision Note

Test yourself

Author

Katie M

Last updated

7 November 2024

Latent Heat Capacity

Energy is required to change the state of a substance
Examples of changes of state are:
- Melting = solid to liquid
- Evaporation / vaporisation / boiling = liquid to gas
- Sublimation = solid to gas
- Freezing = liquid to solid
- Condensation = gas to liquid

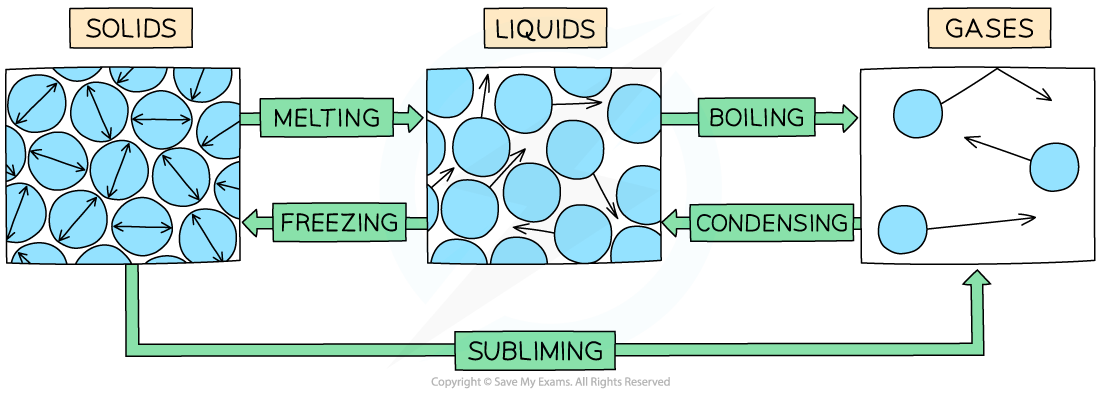
The example of changes of state between solids, liquids and gases

When a substance changes state, there is no temperature change
The energy supplied to change the state is called the latent heat and is defined as:
The thermal energy required to change the state of 1 kg of mass of a substance without any change of temperature
There are two types of latent heat:
- Specific latent heat of fusion (melting)
- Specific latent heat of vaporisation (boiling)
The larger the mass of the substance, the more energy will be required to change its state. Hence why specific latent heat is defined by 1 kg

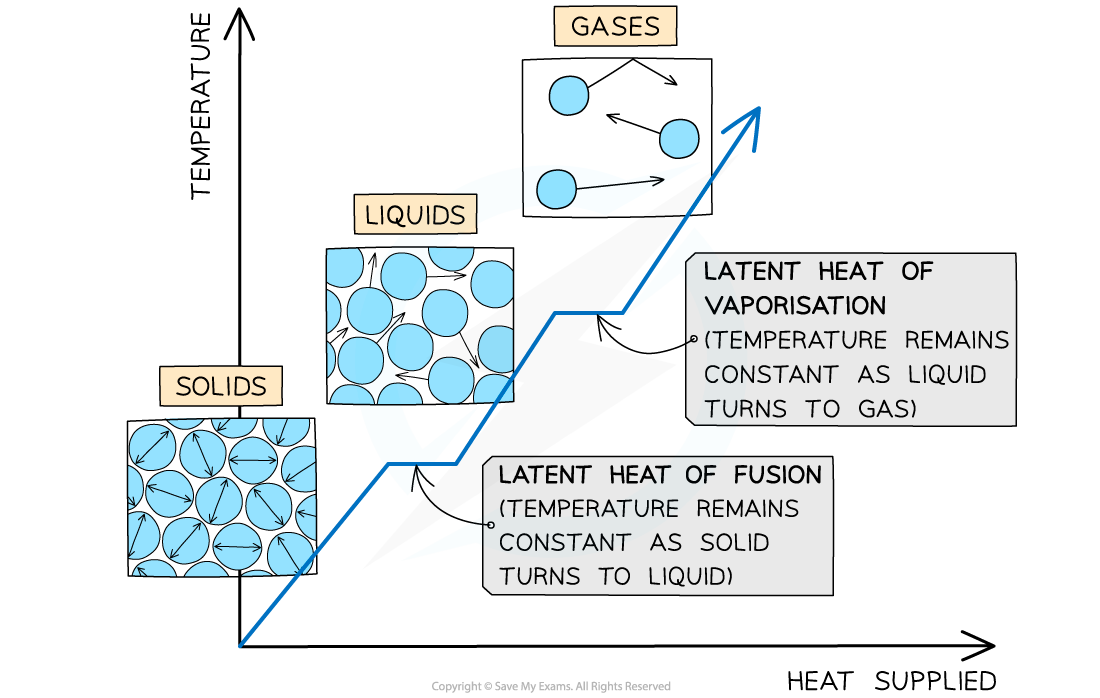
Latent heat graph, downloadable AS & A Level Physics revision notes

The changes of state with heat supplied against temperature. There is no change in temperature during changes of state

The horizontal line of the latent heat of fusion represents melting (if heat is supplied) or freezing (if heat is removed)
The horizontal line of the latent heat of vaporisation represents evaporation (if heat is supplied) or condensation (if heat is removed)

The specific latent heat of fusion is defined as:
The thermal energy required to convert 1 kg of solid to liquid with no change in temperature
Latent heat of fusion applies to:
- Melting a solid
- Freezing a liquid
The specific latent heat of vaporisation is defined as:
The thermal energy required to convert 1 kg of liquid to gas with no change in temperature
Latent heat of vaporisation applies to:
- Vaporising a liquid
- Condensing a gas

Calculating Specific Latent Heat

The amount of energy Q required to melt or vaporise a mass of m with latent heat L is:

Q = mL

Where:
- Q = amount of thermal energy to change the state (J)
- m = mass of the substance changing state (kg)
- L = latent heat of fusion or vaporisation (J kg^-1)

The values of latent heat for water are:
- Specific latent heat of fusion = 330 kJ kg^-1
- Specific latent heat of vaporisation = 2.26 MJ kg^-1
Therefore, evaporating 1 kg of water requires roughly seven times more energy than melting the same amount of ice to form water
The reason for this is to do with intermolecular forces:
- When ice melts: energy is required to just increase the molecule separation until they can flow freely over each other
- When water boils: energy is required to completely separate the molecules until there are no longer forces of attraction between the molecules, hence this requires much more energy. Vaporisation is also doing work against atmospheric pressure
More energy has to be supplied to separate molecules than break a solid bond, which is why the latent heat of vaporisation of water is much greater than the specific latent heat of fusion of water

Thermal Equilibrium

A common scenario in exam questions is the mixing of two substances and the resulting transfer of thermal energy
After a long enough period of time, the materials in the system will reach thermal equilibrium
- This means they both have the same final temperature
When performing these calculations, it is important to consider the sign of the energy changes
- If ice is dropped into a warm drink, for example, energy is transferred to the ice, while energy is transferred away from the warm drink
- In calculations, this difference in direction is indicated with a negative sign

$Δ Q_{c o l d e r} = - Δ Q_{w a r m e r}$

Where:
- $Δ Q_{c o l d e r}$ is the energy required to raise the temperature of the colder material in the mixture
- $Δ Q_{w a r m e r}$ is the energy released by the warmer material in the mixture
Additionally, if one of the materials changes phase, this must be included in the calculation as well
- For example, if the colder material is a solid and it melts before thermal equilibrium is reached, the equation becomes:

$Δ Q_{c o l d e r, s o l i d} + Δ Q_{m e l t i n g} + Δ Q_{c o l d e r, l i q u i d} = - Δ Q_{w a r m e r}$

Where:
- $Δ Q_{c o l d e r, s o l i d}$ is the energy needed to raise the temperature of the solid colder material to its melting point
- $Δ Q_{m e l t i n g}$ is the energy needed for a phase change, melting in this case
- $Δ Q_{c o l d e r, l i q u i d}$ is the energy needed to raise the temperature of the colder material, now in a liquid phase

Worked Example

The energy needed to boil a mass of 530 g of a liquid is 0.6 MJ. Calculate the specific latent heat of the liquid and state whether it is the latent heat of vaporisation or fusion.

Answer:

Step 1: Write the thermal energy required to change state equation

Q = mL

Step 2: Rearrange for latent heat

$L = \frac{Q}{m}$

Step 3: Substitute in values

m = 530 g = 530 × 10^-3 kg

Q = 0.6 MJ = 0.6 × 10⁶ J

$L = \frac{0.6 \times 10^{6}}{530 \times 10^{- 3}} = 1.132 \times 10^{6} J {kg}^{- 1} = 1.1 MJ {kg}^{- 1} (2 s . f .)$

L is the latent heat of vaporisation because the change in state is from liquid to gas (boiling)

Worked Example

In a coffee shop, someone orders an iced coffee. The barista makes 200 g of coffee at a temperature of 90 °C and then places 6 ice cubes into the cup.

The ice cubes have a mass of 14.5 g each and are kept at a temperature of −5.0 °C in a freezer.

Determine the final temperature of the iced coffee when it reaches thermal equilibrium, assuming no energy is transferred to or from the surroundings.

Specific heat capacity of coffee = 4180 J kg⁻¹ K⁻¹

Specific heat capacity of water = 4190 J kg⁻¹ K⁻¹

Specific heat capacity of ice = 2090 J kg⁻¹ K⁻¹

Latent heat of fusion of ice = 334 J g⁻¹

Answer:

Step 1: List the known quantities

Mass of coffee, m_c = 200 g = 0.20 kg
Initial temperature of coffee, T_c1 = 90 °C
Number of ice cubes = 6
Mass of a single ice cube, m_i = 14.5 g = 0.0145 kg
Initial temperature of ice, T_i1 = −5.0 °C
Specific heat capacity of coffee, c_c = 4180 J kg⁻¹ K⁻¹
Specific heat capacity of water, c_w = 4190 J kg⁻¹ K⁻¹
Specific heat capacity of ice, c_i = 2090 J kg⁻¹ K⁻¹
Latent heat of fusion of ice, L_i = 334 J g⁻¹ = 334 000 J kg⁻¹

Step 2: Write an expression relating energy gained by ice and energy lost by coffee

Energy gained by ice = −energy lost by coffee
- When thermal equilibrium is reached, the ice will have melted
To reach thermal equilibrium, the ice will be heated to 0 °C, then melt, then the molecules of the ice, in liquid form, will be heated to reach the final equilibrium temperature
In equation form, this is written as:

$Q_{h e a t i c e} + Q_{m e l t i c e} + Q_{h e a t w a t e r} = - Q_{c o f f e e}$

Substitute the equations for energy required to raise temperature and energy required to change state:

$6 m_{i} c_{i} (0 - (- 5)) + 6 m_{i} L_{i} + 6 m_{i} c_{w} (T_{f} - 0) = - m_{c} c_{c} (T_{f} - 90)$

Where T_f is the temperature of the mixture at thermal equilibrium
Simplifying the above gives:

$30 m_{i} c_{i} + 6 m_{i} L_{i} + 6 m_{i} c_{w} T_{f} = m_{c} c_{c} (90 - T_{f})$

Step 3: Substitute the known quantities and then rearrange for final temperature

With values from the known values list, the above equation becomes:

$909.15 + 29058 + 364.53 T_{f} = 75240 - 836 T_{f}$

Rearranging for final temperature gives:

$T_{f} = \frac{45272.85}{1200.53} = 37.7 ° C$

A quick "common-sense check" tells us that this temperature is lower than the initial temperature of coffee and higher than the initial temperature of the ice, so is a reasonable answer

Examiner Tips and Tricks

Use these reminders to help you remember which type of latent heat is being referred to:

Latent heat of fusion = imagine ‘fusing’ the liquid molecules together to become a solid
Latent heat of vaporisation = “water vapour” is steam, so imagine vaporising the liquid molecules into a gas

Remember to always include 'without a change in temperature', or words to that effect, within your definitions for latent heat to gain full marks.

Energy Transfers During Phase Changes

When a substance is heated, the molecules are given more energy in the form of kinetic and potential energy
During a change of state (or a phase change), the key points to remember are:
- There is no change in temperature
- The potential energies of the molecules change, but not their kinetic energies
The potential energy of the molecules is due to their separation and intermolecular bonds
- Since they move further apart (evaporation) or closer together (condensation), their potential energy will change as a result of this
The heat absorbed in melting and boiling causes the molecules to move further apart by overcoming the intermolecular forces of attraction
The heat released in freezing and condensation allows the molecules to move closer together and the intermolecular forces of attraction become stronger
- This is because the kinetic energy is proportional to the temperature
- If there is no change in temperature, there must be no change in kinetic energy either

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: