Specific Heat Capacity (AQA A Level Physics)

Specific Heat Capacity

• When a substance is heated, its temperature rises causing the particles within it to gain kinetic energy

  • The amount of energy required to raise the temperature of a substance is given by its specific heat capacity

• The specific heat capacity of a substance is defined as:

  The amount of thermal energy required to raise the temperature of 1 kg of a substance by 1 °C (or 1 K) without a change of state

• This quantity determines the amount of energy needed to change the temperature of a substance

• Specific heat capacity has the symbol c and is measured in units of Joules per kilogram per Kelvin (J kg^–1 K^–1) or Joules per kilogram per Celsius (J kg^–1 °C^–1)

  • Different substances have different specific heat capacities

  • Specific heat capacity is mainly used for liquids and solids

• From the definition of specific heat capacity, it follows that:

  • The heavier the material, the more thermal energy required to raise its temperature

  • The larger the change in temperature, the higher the thermal energy required to achieve this change

Calculating Specific Heat Capacity

• The amount of thermal energy Q needed to raise the temperature by Δθ for a mass m with specific heat capacity c is equal to:

ΔQ = mcΔθ

• Where:

  • ΔQ = change in thermal energy (J)

  • m = mass of the substance you are heating up (kg)

  • c = specific heat capacity of the substance (J kg^–1 K^–1 or J kg^–1 °C^–1)

  • Δθ = change in temperature (K or °C)

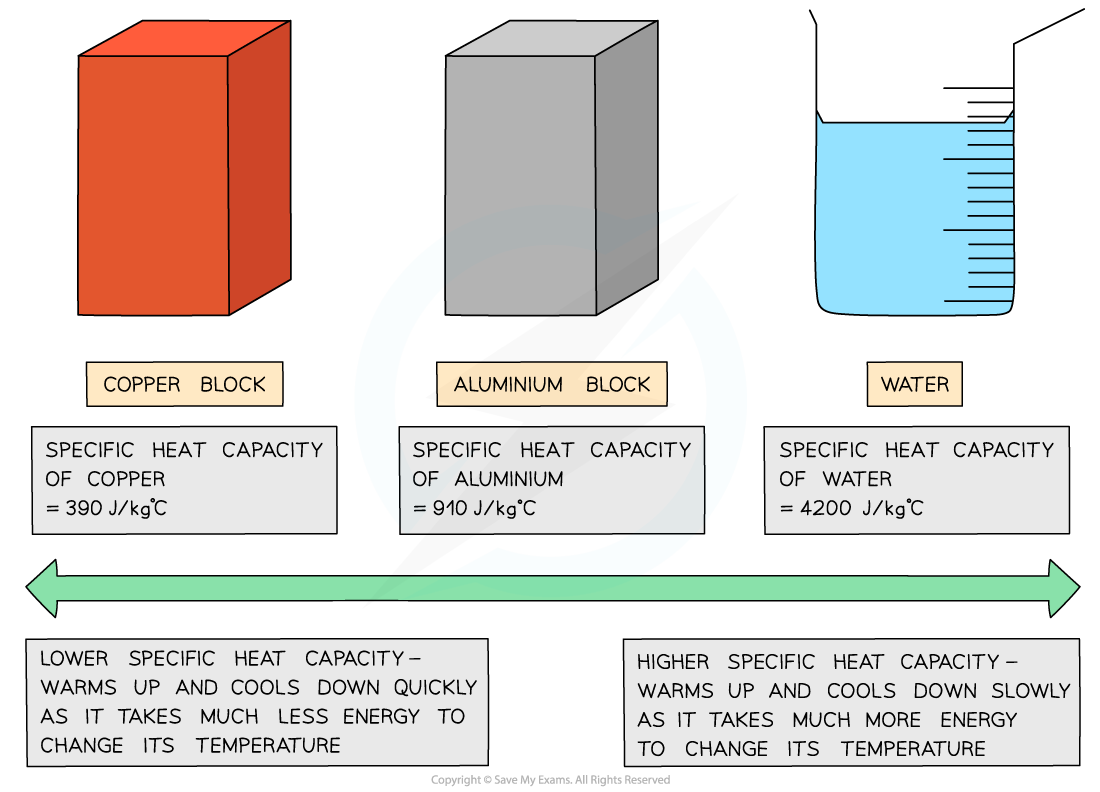
Low v high specific heat capacity

• If a substance has a low specific heat capacity, it heats up and cools down quickly

• If a substance has a high specific heat capacity, it heats up and cools down slowly

• The specific heat capacity of different substances determines how useful they would be for a specific purpose eg. choosing the best material for kitchen appliances

Table of values of specific heat capacity for various substances

• Good electrical conductors, such as copper and lead, are excellent conductors of heat due to their low specific heat capacity

Continuous Flow

• The specific heat capacity of a fluid can be found using a continuous-flow calorimeter

• A fluid flows continuously over a heating element where energy is transferred to the fluid

  • It is assumed that the heat transferred from the apparatus to the surroundings is constant

• For this experiment, the flow rate and the potential difference are changed to ensure the change in temperature of the fluid is kept constant

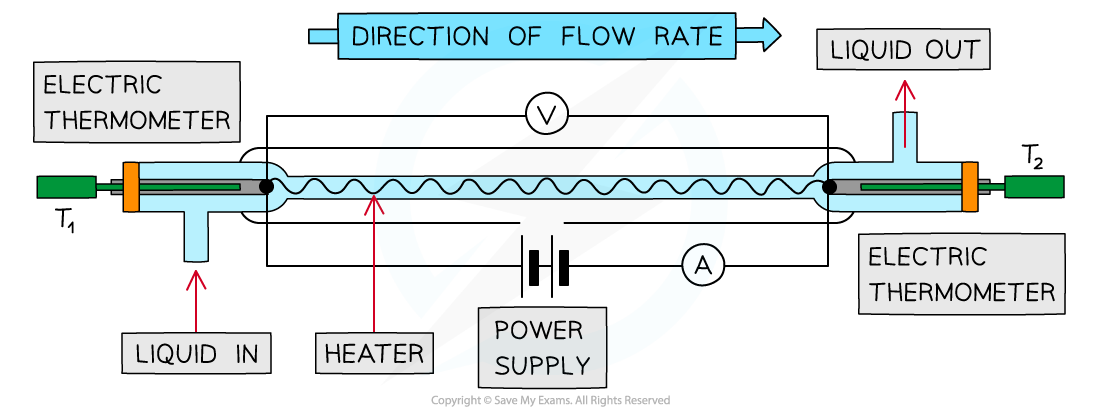
A continuous-flow calorimeter

• A fluid flows through an electrical heating wire. The rise in temperature of the fluid is measured using the electric thermometers and is calculated by:

Δθ = T₂ – T₁

• To find the mass of the fluid, the flow rate (mass leaving the right hand side per second) is recorded and multiplied by the time taken t to give the mass of the fluid that flows in as m₁

• The current I and potential difference V are also recorded

• The flow rate is then altered to give a mass m₂ and the potential difference of the power supply is changed so the temperature difference, Δθ stays the same

• The specific heat capacity is found by assuming the thermal losses to the surroundings are constant for both flow rates

• For the first flow rate, the electrical energy supplied to the fluid in time t₁ is:

I₁V₁t₁ = Q₁ = m₁cΔθ + E_lost

• Where E_lost is the thermal energy lost to the surroundings and I₁V₁ represents the electrical power of the heater

• The second flow rate is:

I₂V₂t₂ = Q₂ = m₂cΔθ + E_lost

• Since E_lost is assumed to be the same, subtracting the first flow rate equation from the second gives the equation:

I₂V₂t₂ – I₁V₁t₁ = Q₂ – Q₁ = (m₂ – m₁)cΔθ

• Rearranging this for the specific heat capacity of the fluid, c gives the final equation: