Resonance (AQA A Level Physics): Revision Note

Resonance

• The frequency of forced oscillations is referred to as the driving frequency (f) or the frequency of the applied force

• All oscillating systems have a natural frequency (f₀), this is defined as this is the frequency of an oscillation when the oscillating system is allowed to oscillate freely

• Oscillating systems can exhibit a property known as resonance

• When the driving frequency approaches the natural frequency of an oscillator, the system gains more energy from the driving force

  • Eventually, when they are equal, the oscillator vibrates with its maximum amplitude, this is resonance

• Resonance is defined as:

  When the frequency of the applied force to an oscillating system is equal to its natural frequency, the amplitude of the resulting oscillations increases significantly

• For example, when a child is pushed on a swing:

  • The swing plus the child has a fixed natural frequency

  • A small push after each cycle increases the amplitude of the oscillations to swing the child higher. This frequency at which this push happens is the driving frequency

  • When the driving frequency is exactly equal to the natural frequency of the swing oscillations, resonance occurs

  • If the driving frequency does not quite match the natural frequency, the amplitude will increase but not to the same extent as when resonance is achieved

• This is because, at resonance, energy is transferred from the driver to the oscillating system most efficiently

  • Therefore, at resonance, the system will be transferring the maximum kinetic energy possible

• A graph of driving frequency f against amplitude A of oscillations is called a resonance curve. It has the following key features:

  • When f < f₀, the amplitude of oscillations increases

  • At the peak where f = f₀, the amplitude is at its maximum. This is resonance

  • When f > f₀, the amplitude of oscillations starts to decrease

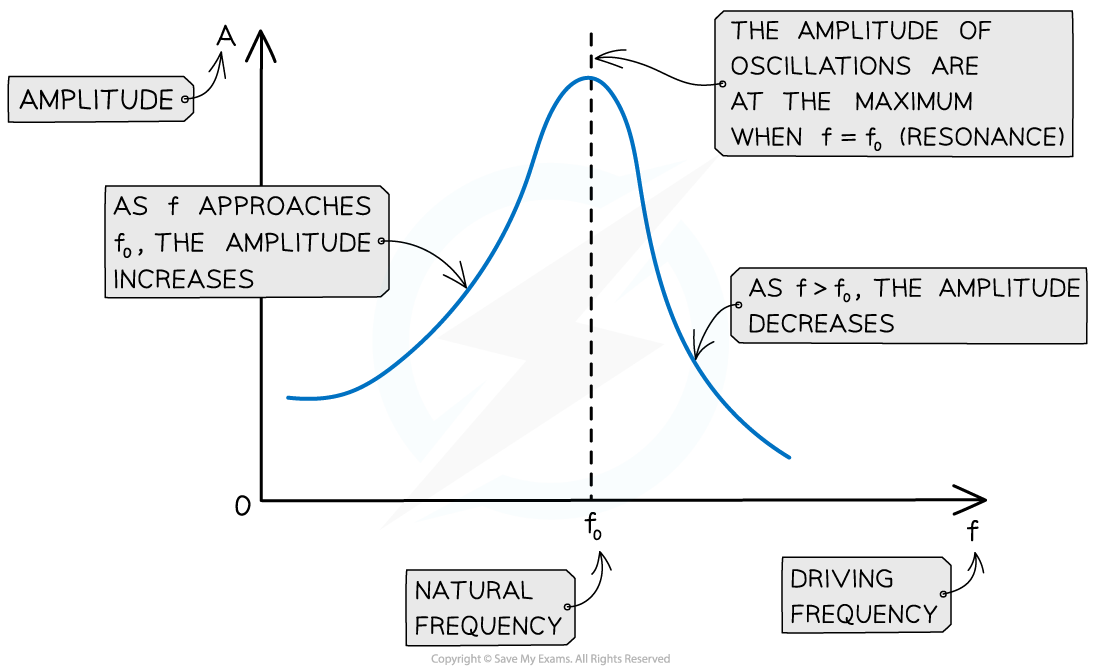
The maximum amplitude of the oscillations occurs when the driving frequency is equal to the natural frequency of the oscillator

The Effects of Damping on Resonance

• Damping reduces the amplitude of resonance vibrations

• The height and shape of the resonance curve will therefore change slightly depending on the degree of damping

  • Note: the natural frequency f₀ of the oscillator will remain the same

• As the degree of damping is increased, the resonance graph is altered in the following ways:

  • The amplitude of resonance vibrations decrease, meaning the peak of the curve lowers

  • The resonance peak broadens

  • The resonance peak moves slightly to the left of the natural frequency when heavily damped

• Therefore, damping reduced the sharpness of resonance and reduces the amplitude at resonant frequency

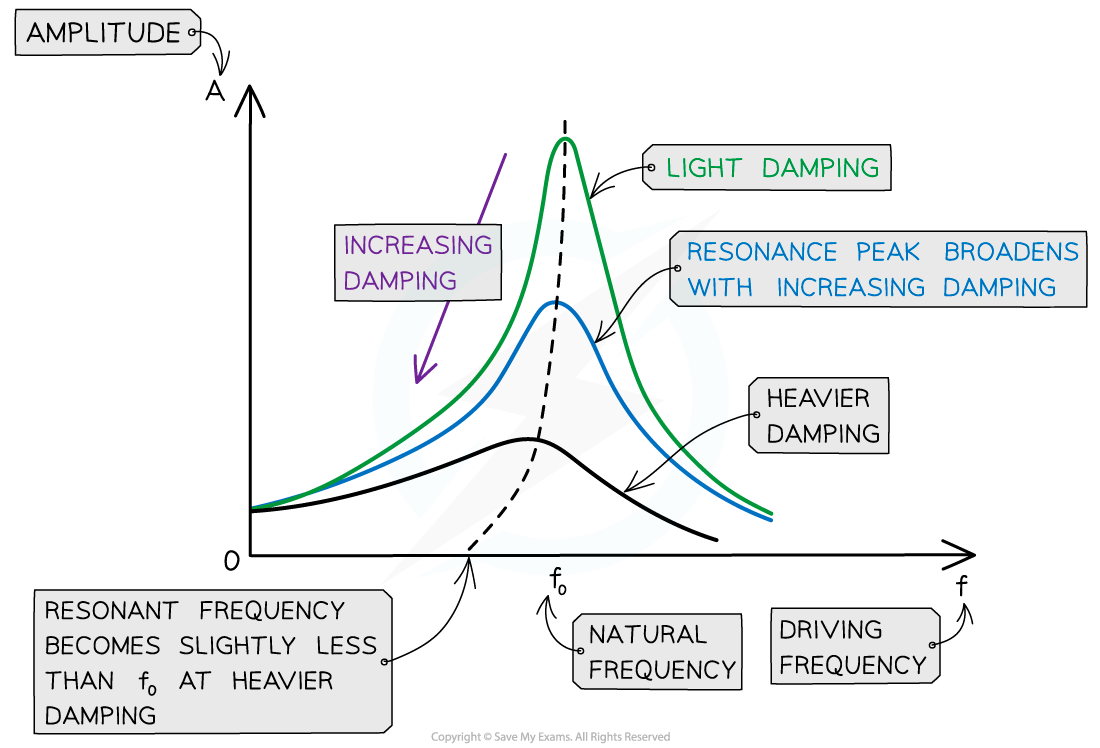
As damping is increased, resonance peak lowers, the curve broadens and moves slightly to the left

Resonance Effects

• Resonance occurs for any forced oscillation where the frequency of the driving force is equal to the natural frequency of the oscillator

• Examples include:

  • An organ pipe, where air resonates down an air column setting up a stationary wave in the pipe

  • Glass smashing from a high pitched sound wave at the right frequency

  • A radio tuned so that the electric circuit resonates at the same frequency as the specific broadcast

Standing waves forming inside an organ pipe from resonance

• A mechanical system commonly used to show resonance is Barton's pendulums

• A set of light pendulums labelled A-E are suspended from a string

  • A heavy pendulum X, with a length L, is attached to the string at one end and will act as the driving pendulum

• When pendulum X is released, it pushes the string and begins to drive the other pendulums

• Most of the pendulums swing with a low amplitude but pendulum C with the same length L has the largest amplitude

  • This is because its natural frequency is equal to the frequency of pendulum X (the driving frequency)

Barton's pendulums helps display resonance

• The phase of the oscillations relative to the driver are:

  • Pendulums E and D with lengths < L are in phase

  • Pendulum C with length = L is 0.5π out of phase

  • Pendulums B and A with lengths > L are π out of phase