Calculating Maximum Speed & Acceleration (AQA A Level Physics)

Revision Note

Test yourself

Author

Ashika

Last updated

7 November 2024

Maximum Speed

The maximum speed of an oscillator, v_max, is given by the equation:

v_max = ωA

Where:
- v_max = maximum speed (m s^-1)
- ω = angular frequency (rad s^-1)
- A = amplitude (m)
This comes from the SHM speed-equation

$v = \pm ω \sqrt{(A^{2} - x^{2})}$

Where:
- v is maximum at the equilibrium position x = 0
- So,

$v_{m a x} = \pm ω \sqrt{A^{2}} = ω A$

When an oscillator begins its motion at the equilibrium position then the velocity-time graph is a cosine graph

$v = v_{0} \cos (ω t)$

The maximum speed of an oscillator is the amplitude, v₀of the velocity-time graph
For a mass oscillating on a vertical spring:
- v_max occurs when the spring is in its equilibrium position
- v = 0 at the amplitude position

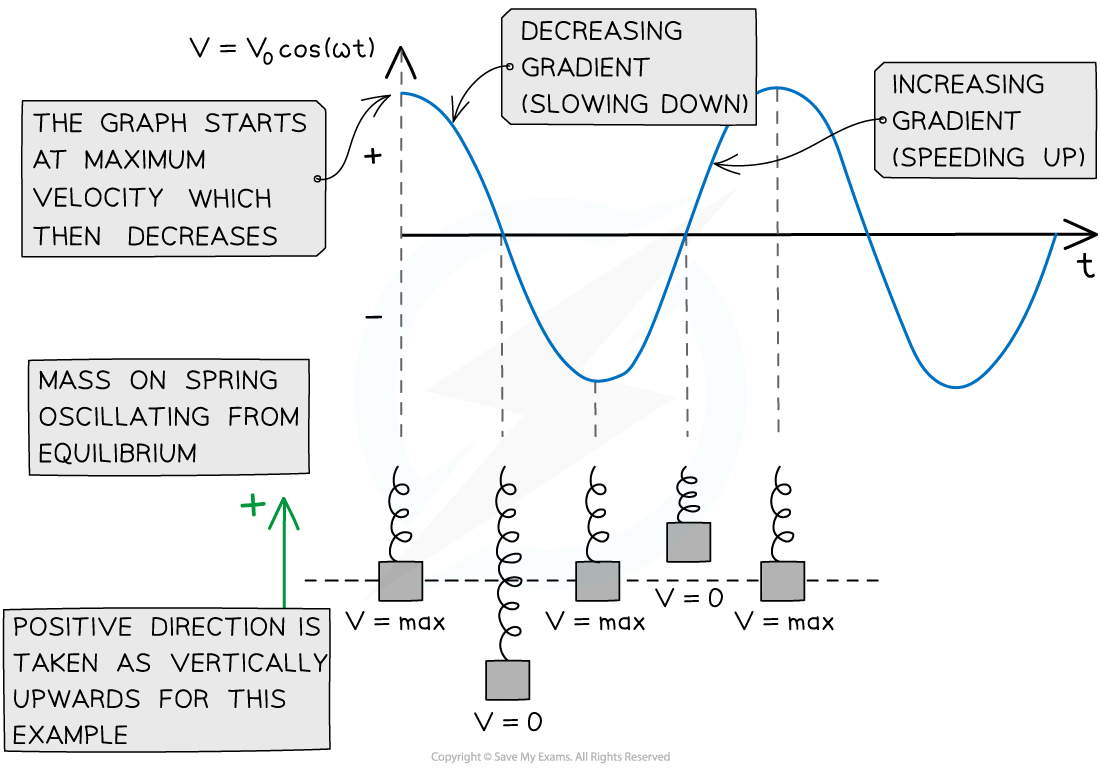
Speed SHM graph, downloadable AS & A Level Physics revision notes

The maximum speed of a mass on a spring is at the equilibrium position. Its speed is 0 at its positive and negative amplitude

Worked Example

Calculate the frequency of an oscillator with a maximum speed of 12 m s^-1 and amplitude of 1.4 m.

Answer:

Step 1: State the known values

Maximum speed, v_max = 12 m s^-1
Amplitude, A = 1.4 m

Step 2: Write down the equation

v_max = ωA

Step 3: Rewrite angular velocity in terms of frequency f

ω = 2πf

v_max = 2πfA

Step 4: Rearrange for frequency, f

$f = \frac{v_{\max}}{2 πA}$

Step 5: Substitute in the values

$f = \frac{12}{2 π \times 1.4} = 1.364 = 1.4 Hz$

Maximum Acceleration

The maximum acceleration, a_max of an oscillator will occur when the gradient of the velocity-time graph is steepest
- When v = 0 m s⁻¹ at x = A

Acceleration is zero at the equilibrium position (x = 0)

The maximum acceleration is given by the equation:

a_max = ω²A

Where:
- a_max = maximum acceleration (m s²)
- ω = angular frequency (rad s^-1)
- A = amplitude (maximum displacement, x) (m)
This comes from the defining equation of SHM:

a = −ω²x

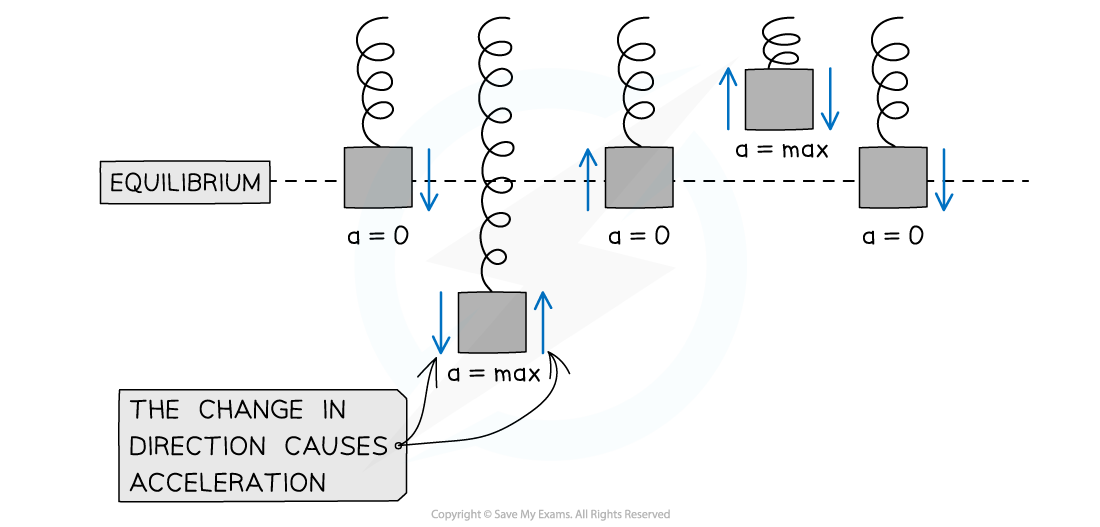
Max & Min Acceleration, downloadable AS & A Level Physics revision notes

The maximum acceleration of a mass on a spring is at its positive and negative amplitude. Its acceleration is 0 at the equilibrium position

Worked Example

Calculate the maximum acceleration of an oscillator with a time period of 0.4 s and amplitude of 2.8 m.

Answer:

Step 1: State the known values

Time period, T = 0.4 s
Amplitude, A = 2.8 m

Step 2: Write down the equation

a_max = ω²A

Step 3: Rewrite maximum acceleration with time period T

$a_{\max} = {(\frac{2 π}{T})}^{2} A$

Step 4: Substitute in the values

$a_{\max} = {(\frac{2 π}{0.4})}^{2} \times 2.8 = 690.97 = 690 m s^{- 2} (2 s . f)$

Examiner Tips and Tricks

Make sure not to get mixed up with lowercase a (acceleration) and uppercase A (amplitude). Make sure you feel confident moving between the equations in their various forms.