Centripetal Force (AQA A Level Physics): Revision Note

Calculating Centripetal Force

• An object moving in a circle is not in equilibrium, it has a resultant force acting upon it

  • This is known as the centripetal force and is what keeps the object moving in a circle

• The centripetal force (F) is defined as:

  The resultant force towards the centre of the circle required to keep a body in uniform circular motion. It is always directed towards the centre of the body's rotation.

•  Centripetal force can be calculated using:

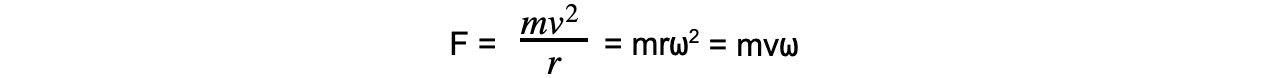
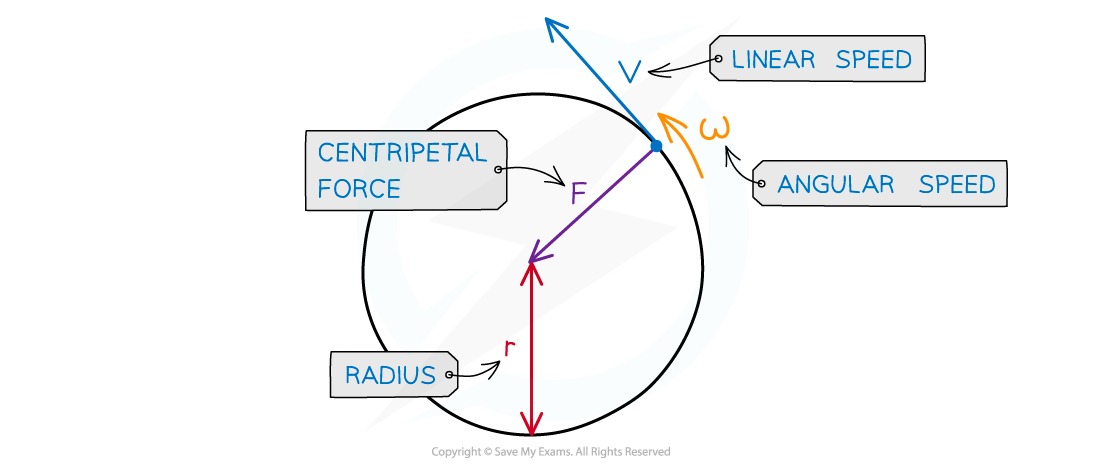
Centripetal force is always perpendicular to the direction of travel

• Where:

  • F = centripetal force (N)

  • v = linear velocity (m s^-1)

  • ⍵ = angular speed (rad s^-1)

  • r = radius of the orbit (m)

• Note: centripetal force and centripetal acceleration act in the same direction

  • This is due to Newton’s Second Law

• The centripetal force is not a separate force of its own

  • It can be any type of force, depending on the situation, which keeps an object moving in a circular path

Examples of centripetal force

• When solving circular motion problems involving one of these forces, the equation for centripetal force can be equated to the relevant force equation

• For example, for a mass orbiting a planet in a circular path, the centripetal force is provided by the gravitational force

• When an object travels in circular motion, there is no work done

  • This is because there is no change in kinetic energy