A LevelPhysicsAQARevision NotesFurther Mechanics & Thermal PhysicsMolecular Kinetic Theory ModelGas Laws v Kinetic Theory

Gas Laws v Kinetic Theory (AQA A Level Physics): Revision Note

Exam code: 7408

Written by: Ashika

Reviewed by: Caroline Carroll

Updated on 2 July 2026

Gas Laws v Kinetic Theory

There is a scientific distinction between the gas laws and kinetic theory

Gas Laws

The gas laws are empirical in nature which means they are based on observation and evidence
The gas laws include Boyle's Law, Charles's Law, Pressure Law and the ideal gas equation
These are all based on observations of how a gas responds to changes in its environment, namely volume, pressure and temperature from experiment

Kinetic Theory

Kinetic theory is based on theory (as stated in its name)
This means it is based on assumptions and derivations from existing theories
These are then used to explain why the gas laws behave the way they do

Ideal Gas Internal Energy

The internal energy of an object is intrinsically related to its temperature
When a container containing gas molecules is heated up, the molecules begin to move around faster, increasing their kinetic energy
If the object is a solid, where the molecules are tightly packed, when heated the molecules begin to vibrate more
Molecules in liquids and solids have both kinetic and potential energy because they are close together and bound by intermolecular forces
However, ideal gas molecules are assumed to have no intermolecular forces
- This means they have no potential energy, only kinetic energy
So the ideal gas internal energy is the sum of all the kinetic energies of the atoms
- In equation form, this can be written as:

$U = N \times E_{k}$

Where:
- U is the internal energy of the ideal gas in joules, J
- N is the number of particles in the ideal gas
- E_k is the average kinetic energy of a single particle in joules, J
Temperature is proportional to average kinetic energy, therefore, for an ideal gas, internal energy is proportional to temperature (this is covered in greater detail in Average Molecular Kinetic Energy)

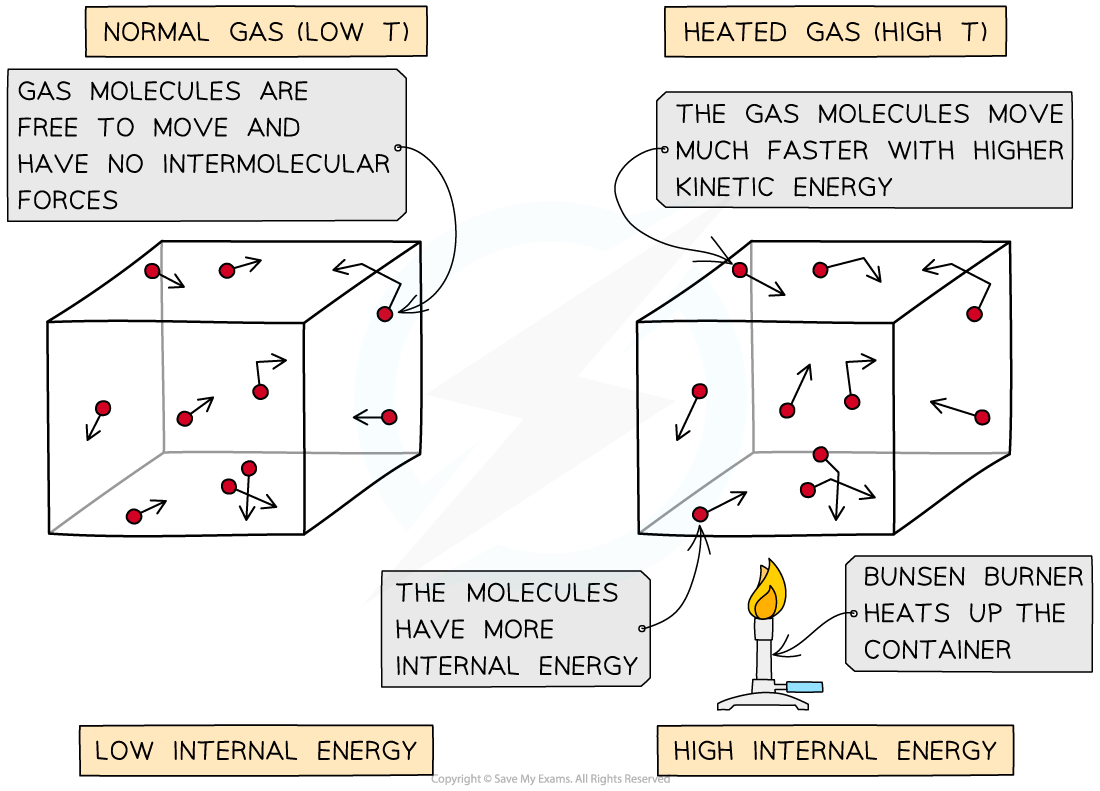
Change in internal energy, downloadable AS & A Level Physics revision notes

As the container is heated up, the gas molecules move faster with higher kinetic energy and therefore higher internal energy

Worked Example

A container is filled with 3.00 moles of ideal gas. Each gas particle has a mass of 6.664 × 10⁻²⁷ kg and an average speed of 1400 m s⁻¹.

Calculate the internal energy of this ideal gas.

Answer:

Step 1: Recall the definition of internal energy for an ideal gas

For an ideal gas, internal energy is the sum of all the kinetic energies of all the particles in the system
- This is because there are no potential energies for an ideal gas, as there are no interactions between particles

Step 2: Calculate the average kinetic energy for a single particle

The kinetic energy of one particle travelling at average speed is:

$E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} \times 6.664 \times 10^{- 27} \times 1400^{2}$

$E_{k} = 6.53072 \times 10^{- 21} J$

Step 3: Calculate the total kinetic energy of all the particles and, therefore, the internal energy of the gas

To find the number of particles, N, use Avogadro's number:

$N = N_{A} n = 6.02 \times 10^{23} \times 3$

$N = 1.806 \times 10^{24}$

The internal energy is therefore:

$U = N \times E_{k} = 1.806 \times 10^{24} \times 6.53072 \times 10^{- 21}$

$U = 11 794 J = 11.8 kJ (3 s . f .)$

Examiner Tips and Tricks

If an exam question about an ideal gas asks for the total internal energy, remember that this is equal to the total kinetic energy since an ideal gas has zero potential energy

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent