Period of Simple Pendulum (AQA A Level Physics): Revision Note

Period of Simple Pendulum

• A simple pendulum consists of a string and a bob at the end

  • The bob is a weight, generally spherical and considered a point mass

  • The bob moves from side to side

  • The string is light and inextensible remaining in tension throughout the oscillations

  • The string is attached to a fixed point above the equilibrium position

• The time period of a simple pendulum for small angles of oscillation is given by:

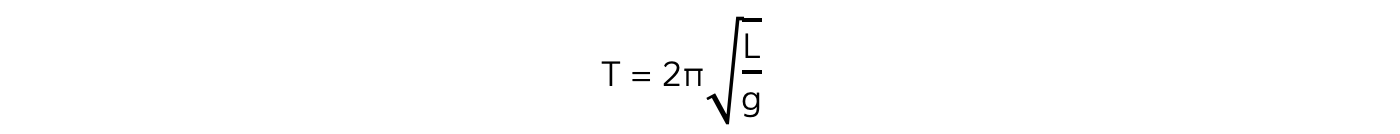
• Where:

  • T = time period (s)

  • L = length of string (from the pivot to the centre of mass of the bob) (m)

  • g = gravitational field strength (N kg^-1)

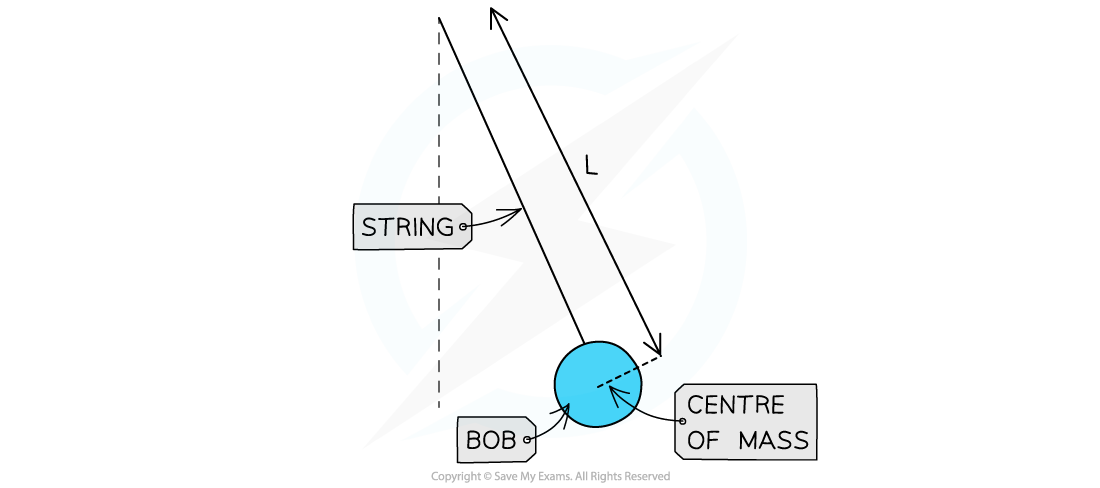
A simple pendulum

• The time period of a pendulum does depend on the gravitational field strength, meaning its period would be different on the Earth and the Moon

Small Angle Approximation

• This formula is limited to small angles (θ < 10°) and therefore small amplitudes of oscillation from the equilibrium point

• The restoring force of the pendulum is the weight component acting along the arc of the circle towards the equilibrium position

• It is resolved to act at an angle θ to the horizontal x 

• When considering SHM because of small angle approximation it is assumed the restoring force acts along the horizontal

• So sin θ ≅ θ 

Forces on a pendulum when it is displaced. Assuming θ < 10°, the small angle approximation can be used to describe the time period of a simple pendulum such as this.