Electromotive Force & Internal Resistance (AQA A Level Physics)

Electromotive Force

• When charge passes through a power supply such as a battery, it gains electrical energy

• The electromotive force (e.m.f) is defined as:

  The amount of chemical energy converted to electrical energy per coulomb of charge (C) when passing through a power supply

• This can also be written as:

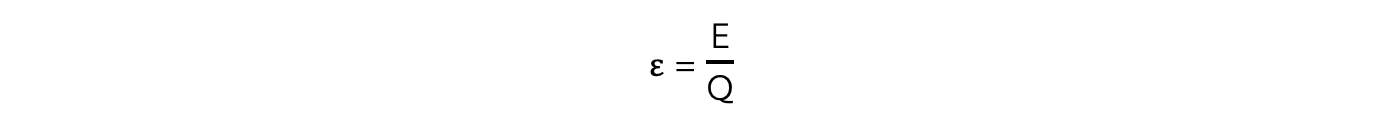
• E.m.f can be represented by the symbol ε (greek letter epsilon)

  • It is not actually a force, and is measured in volts (V)

• E.m.f is equal to the potential difference across the cell when no current is flowing

• E.m.f can be measured by connecting a high-resistance voltmeter around the terminals of the cell in an open circuit, as so:

e.m.f is measured using a voltmeter connected in parallel with the cell

• The terminal potential difference (p.d) is the potential difference across the terminals of a cell

  • If there was no internal resistance, the terminal p.d would be equal to the e.m.f

• It is defined as:

V = IR

• Where:

  • V = terminal p.d (V)

  • I = current (A)

  • R = resistance (Ω)

• Since a cell has internal resistance, the terminal p.d is always lower than the e.m.f

• In a closed circuit, current flows through a cell and a potential difference develops across the internal resistance

• Since resistance opposes current, this reduces the energy per unit charge (voltage) available to the rest of the external circuit

• This difference is called the ‘lost volts'

  • Lost volts is usually represented by little v

  • It is defined as

    The work done per unit charge / coulomb to overcome the internal resistance / resistance inside the battery (when current flows)

  • In other words, this is the voltage lost in the cell due to internal resistance

  • So, from conservation of energy: v = e.m.f − terminal p.d

 v = ε – V = Ir (Ohm’s law)

• Where:

  • v = lost volts (V)

  • I = current (A)

  • r = internal resistance of the battery (Ω)

  • ε = e.m.f (V)

  • V = terminal p.d (V)

• The e.m.f is the sum of these potential differences, giving the equation below:

• E.m.f can therefore be defined as the total, or maximum, voltage available to the circuit

Internal Resistance

• All power supplies have some resistance between their terminals

  • This is called internal resistance (r)

• Internal resistance is defined as:

  The resistance of the materials within the battery

• It is internal resistance that causes the charge circulating to dissipate some electrical energy from the power supply itself

  • This is why the cell becomes warm after a period of time

• Therefore, over time the internal resistance causes loss of voltage or energy loss in a power supply

• A cell can be thought of as a source of e.m.f with an internal resistance connected in series. This is shown in the circuit diagram below:

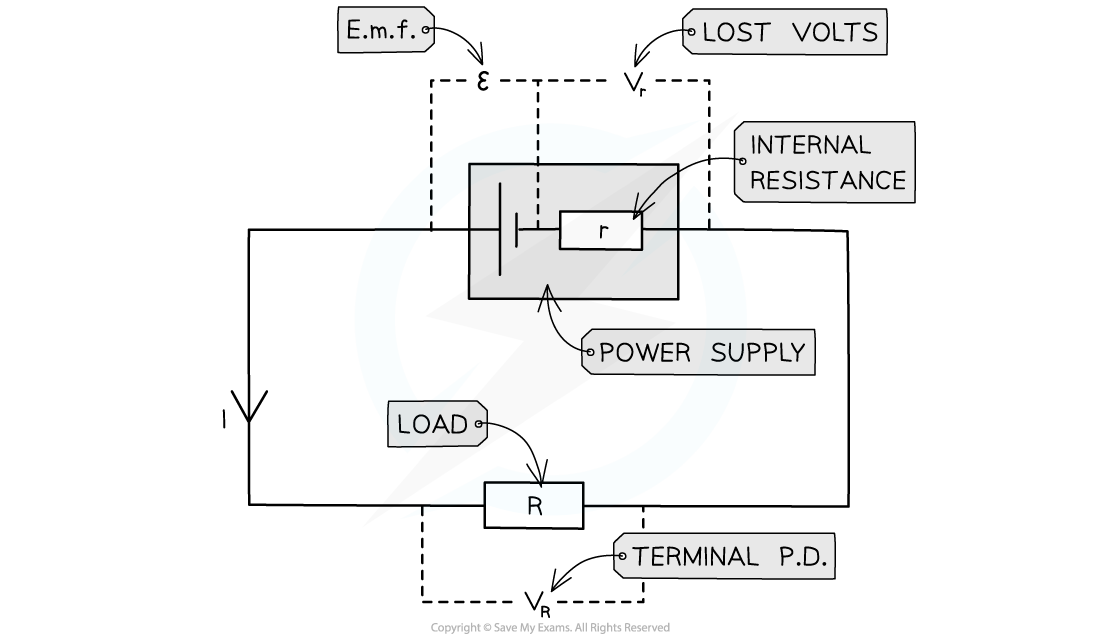
Circuit showing the e.m.f and internal resistance of a power supply

• Where:

  • Resistor R is the 'load resistor'

  • r is the internal resistance

  • ε is the e.m.f

  • V_r is the lost volts

  • V_R is the p.d across the load resistor, which is the same as the terminal p.d