A LevelPhysicsAQARevision NotesMechanics & MaterialsLinear Momentum & ConservationImpulse

Impulse (AQA A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Force & Momentum

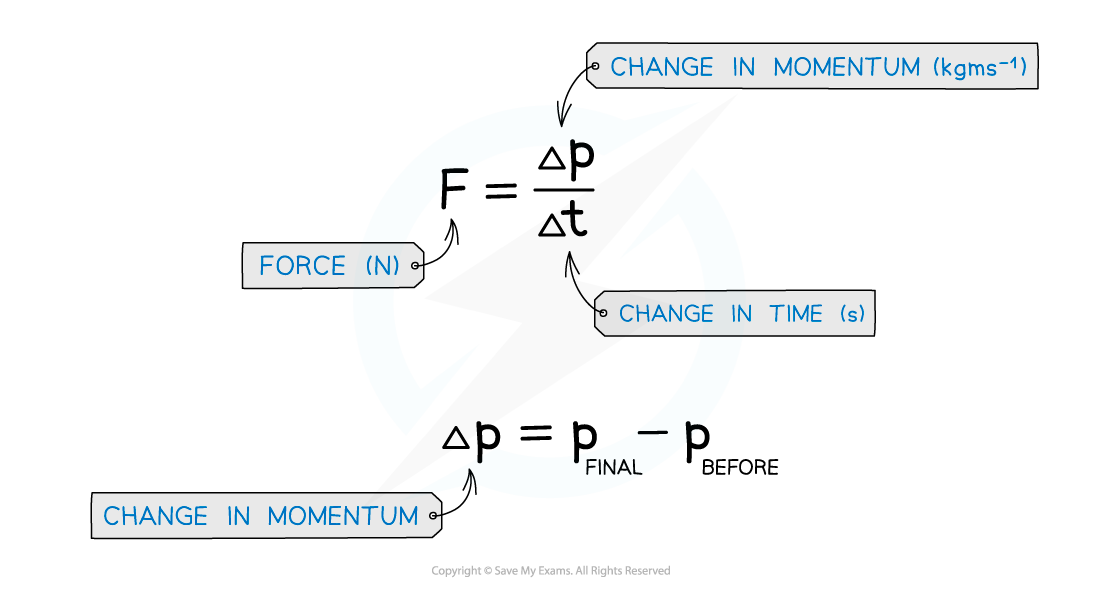
  • Force can also defined as the rate of change of momentum on a body

  • The change in momentum is the final momentum minus the initial momentum

  • These can be expressed as follows:

Force and momentum equation, downloadable AS & A Level Physics revision notes

Direction of Forces

  • Force and momentum are vector quantities with both magnitude and direction 

  • The force that is equal to the rate of change of momentum is still the resultant force

  • The positive direction is taken to be the direction of the initial motion; therefore:

    • a force on an object will be negative if the force opposes its initial velocity

    • the opposing force is exerted by the object it has collided with 

    • the forces will be of equal magnitude and opposite in direction, in accordance with Newton's Third Law

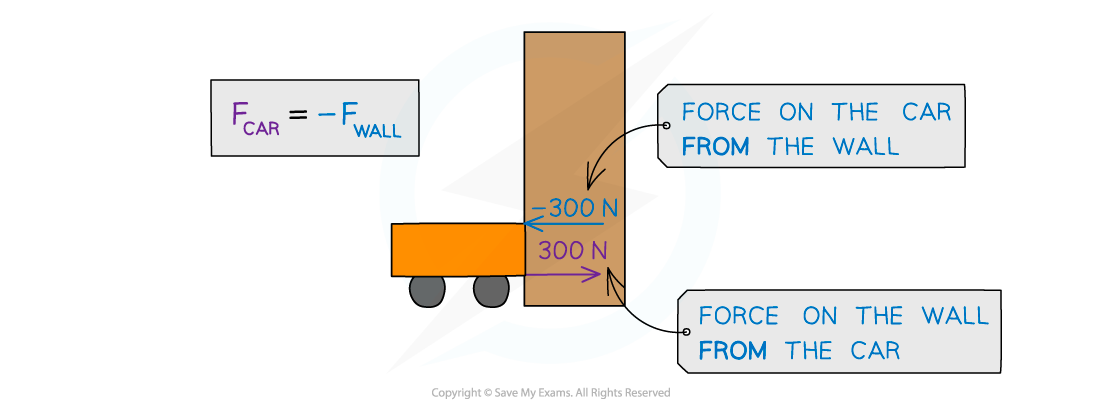
Direction of forces, downloadable AS & A Level Physics revision notes

The car exerts a force on the wall of  300 N, and due to Newton's third law, the wall exerts a force of -300N on the car 

Worked Example

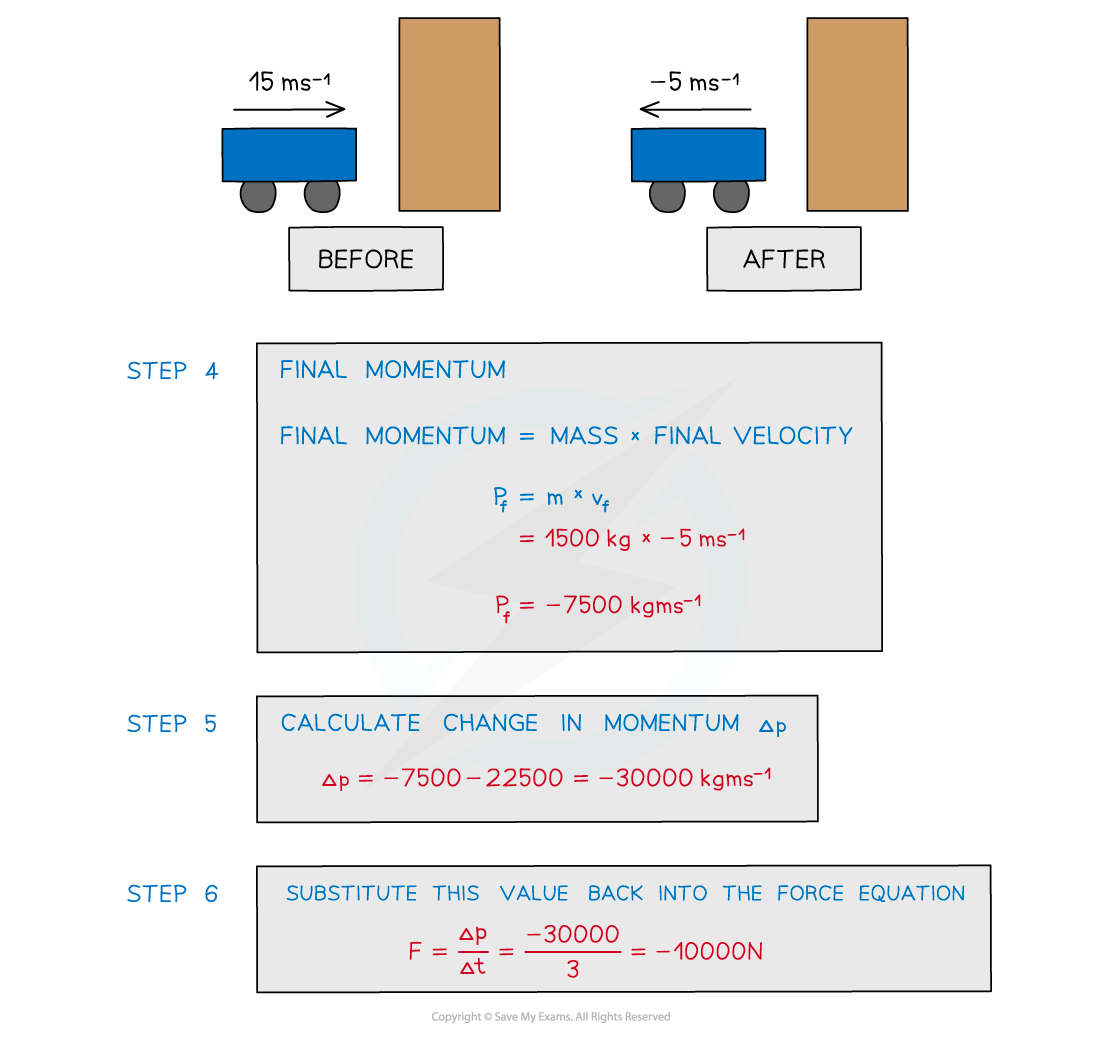
A car of mass 1500 kg hits a wall at an initial velocity of 15 m s-1.

It then rebounds off the wall at 5 m s-1. The car is in contact with the wall for 3.0 seconds.

Calculate the average force experienced by the car.

Answer:

WE - Force on a car answer image (1), downloadable AS & A Level Physics revision notes
Worked example-force on a car (2), downloadable AS & A Level Physics revision notes

Examiner Tips and Tricks

In an exam question, carefully consider what forces are exerted on what objects. Look out for words such as ‘from’, ‘acting on’ or 'exerted on' to determine this, and sketch a quick free body force diagram if you need to.

Impulse

  • When an external resultant force acts on an object for a very short time and changes the object's motion, we call this impulse

    • For example:

      • Kicking a ball

      • Catching a ball

      • A collision between two objects

  • Impulse is the product of the force applied and the time for which it acts

Impulse space equals space F increment t

  • Where:

    • Impulse is measured in newton seconds (N s)

    • F = resultant external force applied, measured in newtons (N)

    • increment t = change in time over which the force acts, measured in seconds (s)

 

  • Because the force is acting for only a short time, it is very difficult to directly measure the magnitude of the force or the time for which it acts

  • Instead, it can be measured indirectly

  • Newtons' second law can be stated in terms of momentum

The resultant force on an object is equal to its rate of change of momentum

  • Therefore:

F space equals space fraction numerator increment p over denominator increment t end fraction space space space rightwards double arrow space space space increment p space equals space F increment t

  • Where:

    • F = resultant force, measured in newtons (N)

    • increment p = change in momentum, measured in kilogram metres per second (kg m s−1) 

    • increment t = change in time over which the force acts, measured in seconds (s)

  • Change in momentum is equal to impulse

  • Therefore, change in momentum can be used to measure impulse indirectly

Impulse space equals space increment p space equals space m v space minus space m u

  • Where:

    • Impulse is measured in newton seconds (N s)

    • increment p = change in momentum, measured in kilogram metres per second (kg m s−1) 

    • m = mass, measured in kilograms (kg)

    • v = final velocity, measured in meters per second (m s−1) 

    • u = initial velocity, measured in meters per second (m s−1) 

  • These equations are only used when the force F is constant

  • Impulse, like force and momentum, is a vector quantity with both a magnitude and direction

  • The impulse is always in the direction of the resultant force

  • A small force acting over a long time has the same effect as a large force acting over a short time

Examiner Tips and Tricks

If you follow the units in your calculations (which is always a good idea!), the base units for the newton are:

1 N = 1 kg m s−2

This is why FΔt = Δp

  • kg m s−2 × s = kg m s−1

Examples of Impulse

  • When rain and hail (frozen water droplets) hit an umbrella they feel very different. This is an example of impulse.

    • Water droplets tend to splatter and roll off the umbrella because there is only a very small change in momentum

    • Hailstones have a larger mass and tend to bounce back off the umbrella, because there is a greater change in momentum

    • Therefore, the impulse that the umbrella applies on the hail stones is greater than the impulse the umbrella applies on the raindrops

    • This means that more force is required to hold an umbrella upright in hail compared to rain

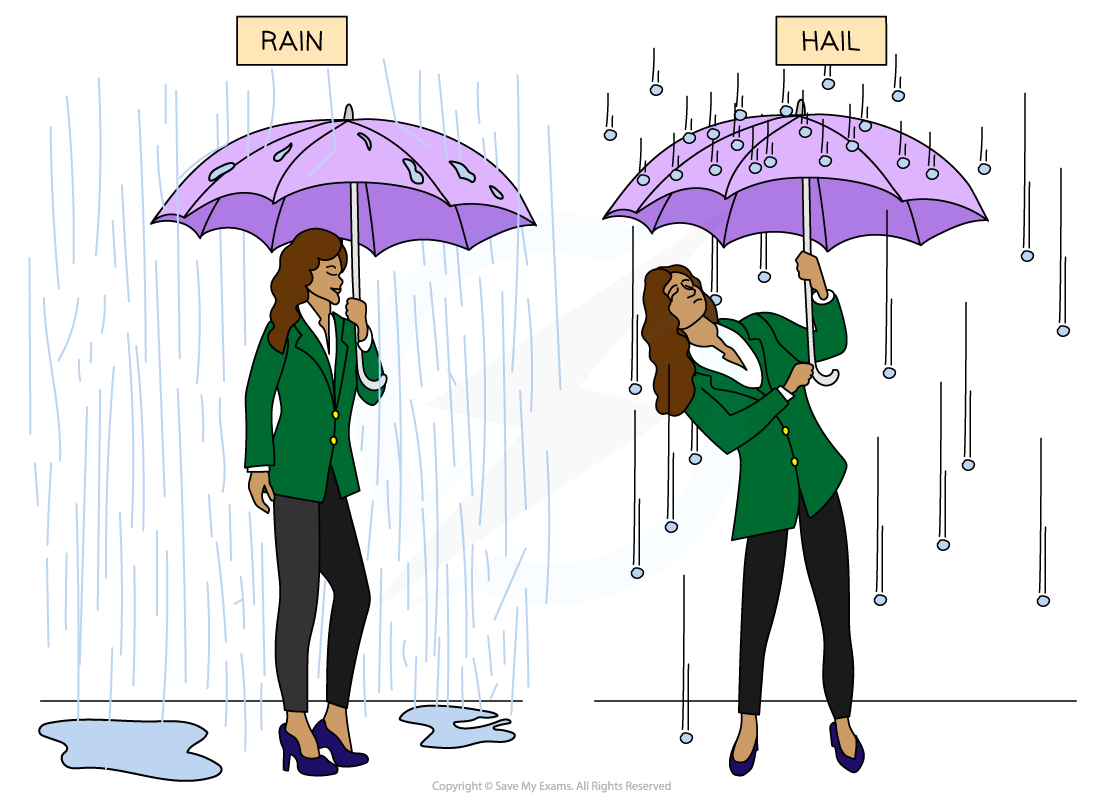
Rain & Hail Impulse, downloadable AS & A Level Physics revision notes

The impulse applied by the umbrella to the hail stones is greater than the impulse applied to the rain drops

  • The concept of impulse is used to prevent injury

    • Increasing the time over which the change in momentum occurs, reduces the force experienced by the person

  • For example, in cricket:

    • A cricket ball travels at very high speeds and therefore has a high momentum

    • When a fielder catches the ball, the ball exerts a force on their hands

    • Stopping a ball with high momentum abruptly will exert a large force on their hands

    • This is because the change in momentum (impulse) acts over a short period of time which creates a large force on the fielder's hands and could cause serious injury

    • A fielder moves their hands back when they catch the ball, which increases the time for the change in momentum to occur

    • This means there will be less force exerted on the fielder's hands and therefore, less chance of injury

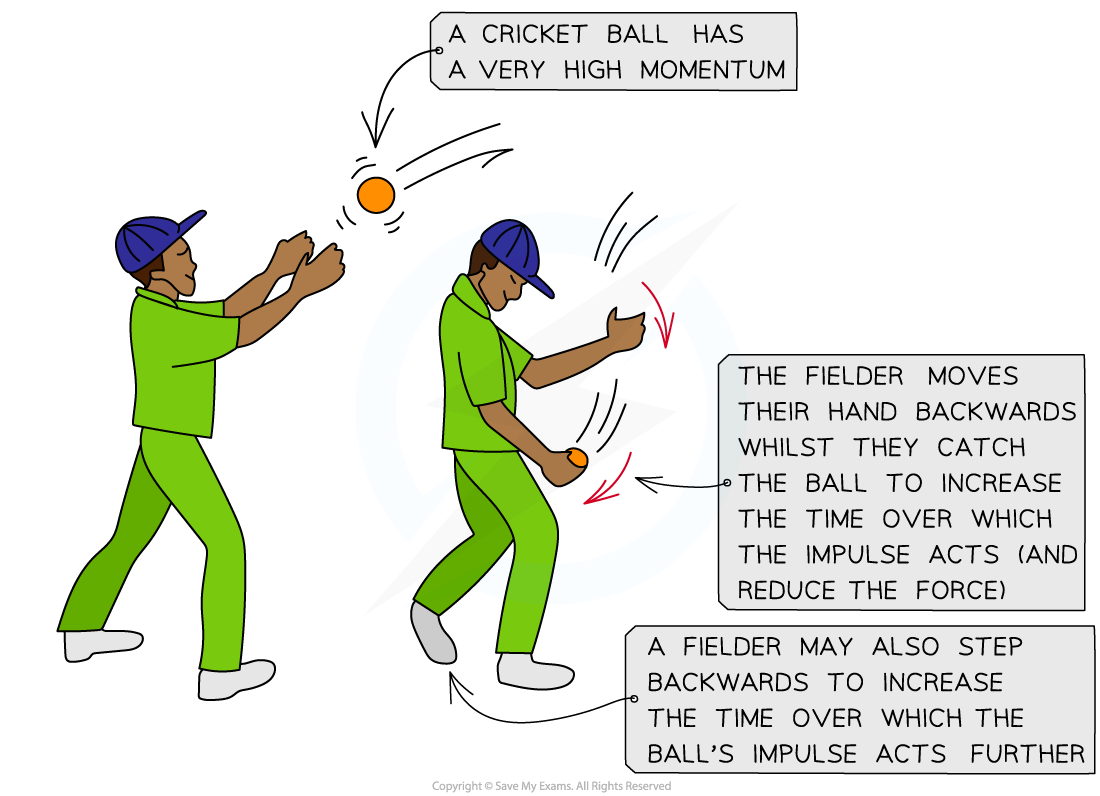
Impulse Cricket Ball

A cricket fielder moves their hands backwards when catching a cricket ball to reduce the force it will exert on their hands

Worked Example

A 58 g tennis ball moving horizontally to the left at a speed of 30 m s–1 is struck by a tennis racket which returns the ball to the right at 20 m s–1.

(a) Calculate the impulse of the racket on the ball 

(b) State the direction of the impulse

Answer:

Part (a)

Step 1: List the known quantities

  • Taking the direction of the initial motion of the ball as positive (the left)

    • Initial velocity, u = 30 m s–1

    • Final velocity, v = –20 m s–1

    • Mass, m = 58 g = 58 × 10–3 kg

Step 2: Write down the impulse equation

Impulse space equals space increment p space equals space m v space minus space m u space equals space m open parentheses v space minus space u close parentheses

Step 3: Substitute in the known values

Impulse space equals space open parentheses 58 space cross times space 10 to the power of negative 3 end exponent close parentheses space cross times space open parentheses negative 20 space minus space 30 close parentheses space equals space minus space 2.9 space straight N thin space straight s

Part(b)

Step 1: State the direction of the impulse

  • Since the impulse is negative, it must be in the opposite direction to which the tennis ball was initially travelling 

  • Therefore, (since the left is taken as positive) the direction of the impulse is to the right

Examiner Tips and Tricks

Remember that if an object changes direction, then this must be reflected by the change in the sign of the velocity (and impulse). This is the most common mistake made by students. Velocity, impulse, force and momentum are all vectors!

For example, if the left is taken as positive and therefore the right as negative, an impulse of 20 N s to the right is equal to −20 N s

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Conservation of MomentumNext:Impulse on a Force-Time Graph
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.