SUVAT Equations
- The SUVAT equations are the equations of motion used for objects in constant acceleration
- They contain the following variables:
- s = displacement (m)
- u = initial velocity (m s-1)
- v = final velocity (m s-1)
- a = acceleration (m s-2)
- t = time (s)
- The 4 SUVAT equations are:
- These are all given on the data sheet
- All the variables, apart from time t, are vector quantities
- This means they can either be positive or negative depending on their direction
- The key terms to look out for are:
- 'Starts from rest', or if the initial velocity is not mentioned, this means u = 0
- 'Starts from rest' means an object starts from rest at x = 0 when t = 0
- If an object is only 'falling due to gravity' then a = g = 9.81 m s-2
- It doesn't matter which way is positive or negative for the scenario, as long as it is consistent for all the vector quantities
- For example, if downwards is negative then for a ball travelling upwards, s must be positive and a must be negative
- SUVAT equations are used for motion with constant acceleration in a straight line
- For example, an object falling in a uniform gravitational field without air resistance
How to Use the SUVAT Equations
- Step 1: Write out the variables that are given in the question, both known and unknown, and use the context of the question to deduce any quantities that aren’t explicitly given
- e.g. for vertical motion a = ± 9.81 m s–2, an object which starts or finishes at rest will have u = 0 or v = 0
- Step 2: Choose the equation which contains the quantities you have listed
- e.g. the equation that links s, u, a and t is s = ut + ½at2
- Step 3: Convert any units to SI units and then insert the quantities into the equation and rearrange algebraically to determine the answer
- Sometimes the question may have to be split into two, where the SUVAT equations will have to be used twice
- For example, if there are two masses connected over a pulley and one mass continues moving after the other has stopped
Worked example
The diagram shows an arrangement to stop trains that are travelling too fast.
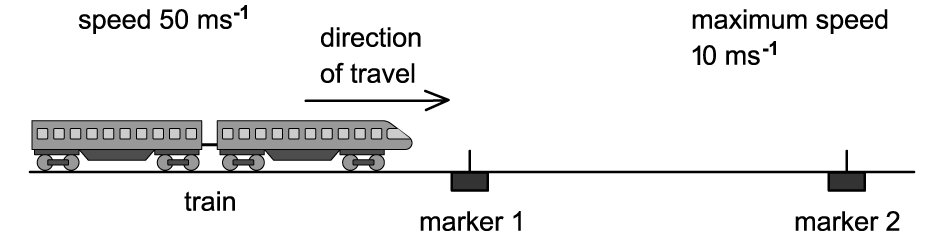
At marker 1, the driver must apply the brakes so that the train decelerates uniformly in order to pass marker 2 at no more than 10 m s–1.
The train carries a detector that notes the times when the train passes each marker and will apply an emergency brake if the time between passing marker 1 and marker 2 is less than 20 s.
Trains coming from the left travel at a speed of 50 m s–1.
Determine how far marker 1 should be placed from marker 2.
Examiner Tip
This is arguably the most important section of this topic, you can always be sure there will be one, or more, questions in the exam about solving problems with SUVAT equations
The best way to master this section is to practice as many questions as possible!
