Resolving Vectors (AQA A Level Physics) : Revision Note
Did this video help you?
Resolving Vectors
Two vectors can be represented by a single resultant vector
Resolving a vector is the opposite of adding vectors
A single resultant vector can be resolved
This means it can be represented by two vectors, which in combination have the same effect as the original one
When a single resultant vector is broken down into its parts, those parts are called components
For example, a force vector of magnitude F and an angle of θ to the horizontal is shown below

The resultant force F at an angle θ to the horizontal
It is possible to resolve this vector into its horizontal and vertical components using trigonometry

The resultant force F can be split into its horizontal and vertical components
For the horizontal component, Fx = F cos θ
For the vertical component, Fy = F sin θ
Forces on an Inclined Plane
Objects on an inclined plane is a common scenario in which vectors need to be resolved
An inclined plane, or a slope, is a flat surface tilted at an angle, θ
Instead of thinking of the component of the forces as horizontal and vertical, it is easier to think of them as parallel or perpendicular to the slope
The weight of the object is vertically downwards and the normal (or reaction) force, R is always vertically up from the object
The weight W is a vector and can be split into the following components:
W cos (θ) perpendicular to the slope
W sin (θ) parallel to the slope
If there is no friction, the force W sin (θ) causes the object to move down the slope
The object is not moving perpendicular to the slope, therefore, the normal force R = W cos (θ)
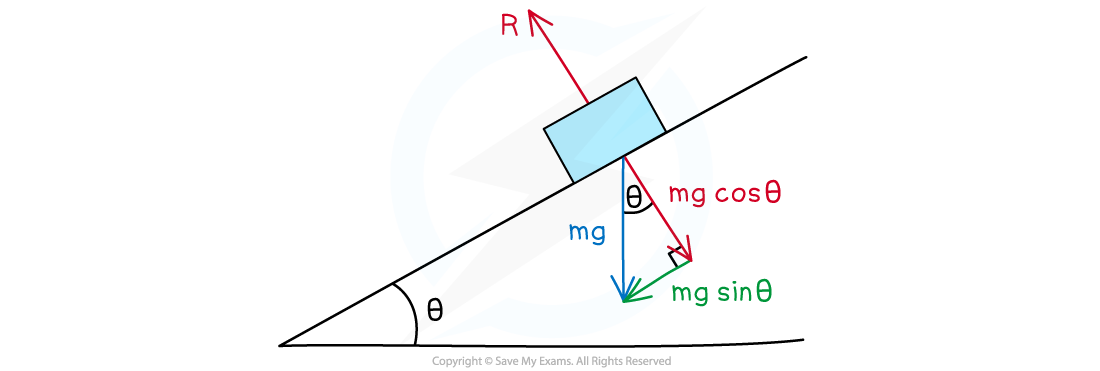
The weight vector of an object on an inclined plane can be split into its components parallel and perpendicular to the slope
Worked Example
A helicopter provides a lift of 250 kN when the blades are tilted at 15º from the vertical.

Calculate the horizontal and vertical components of the lift force.
Answer:
Step 1: Draw a vector triangle of the resolved forces
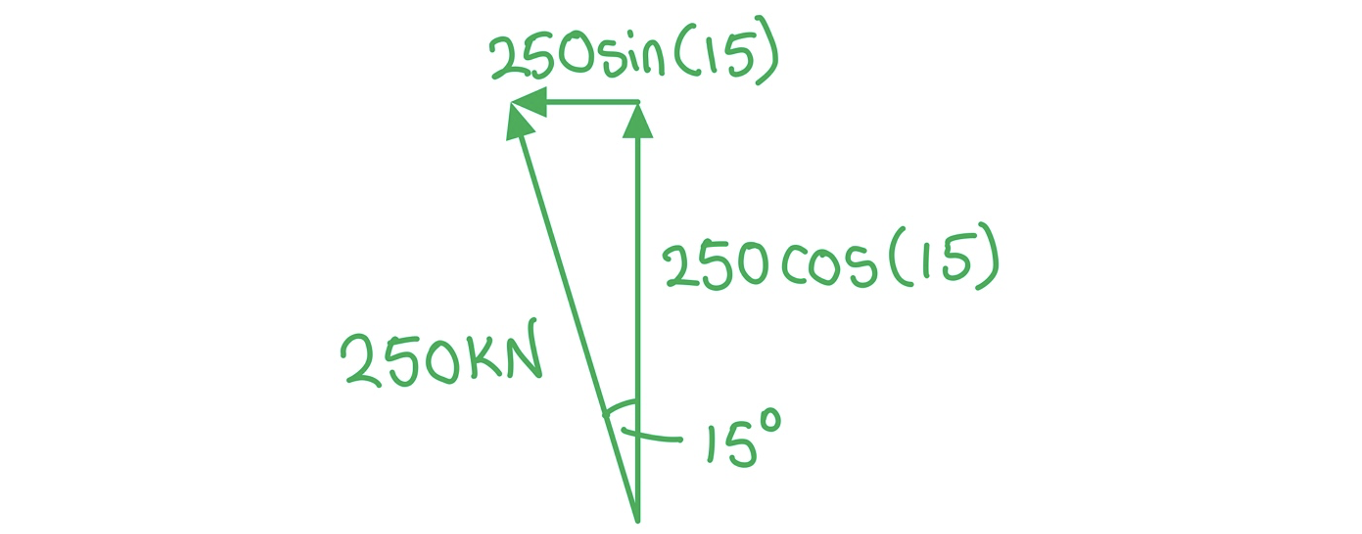
Step 2: Calculate the vertical component of the lift force
Vertical = 250 × cos(15) = 242 kN
Step 3: Calculate the horizontal component of the lift force
Horizontal = 250 × sin(15) = 64.7 kN
Examiner Tips and Tricks
If you're unsure as to which component of the force is cos θ or sin θ, just remember that the cos θ is always the adjacent side of the right-angled triangle AKA, making a 'cos sandwich'

Equilibrium
Coplanar forces can be represented by vector triangles
Forces are in equilibrium if an object is either
At rest
Moving at constant velocity
In equilibrium, coplanar forces are represented by closed vector triangles
The vectors, when joined together, form a closed path
The most common forces on objects are
Weight
Normal reaction force
Tension (from cords and strings)
Friction
The forces on a body in equilibrium are demonstrated below:
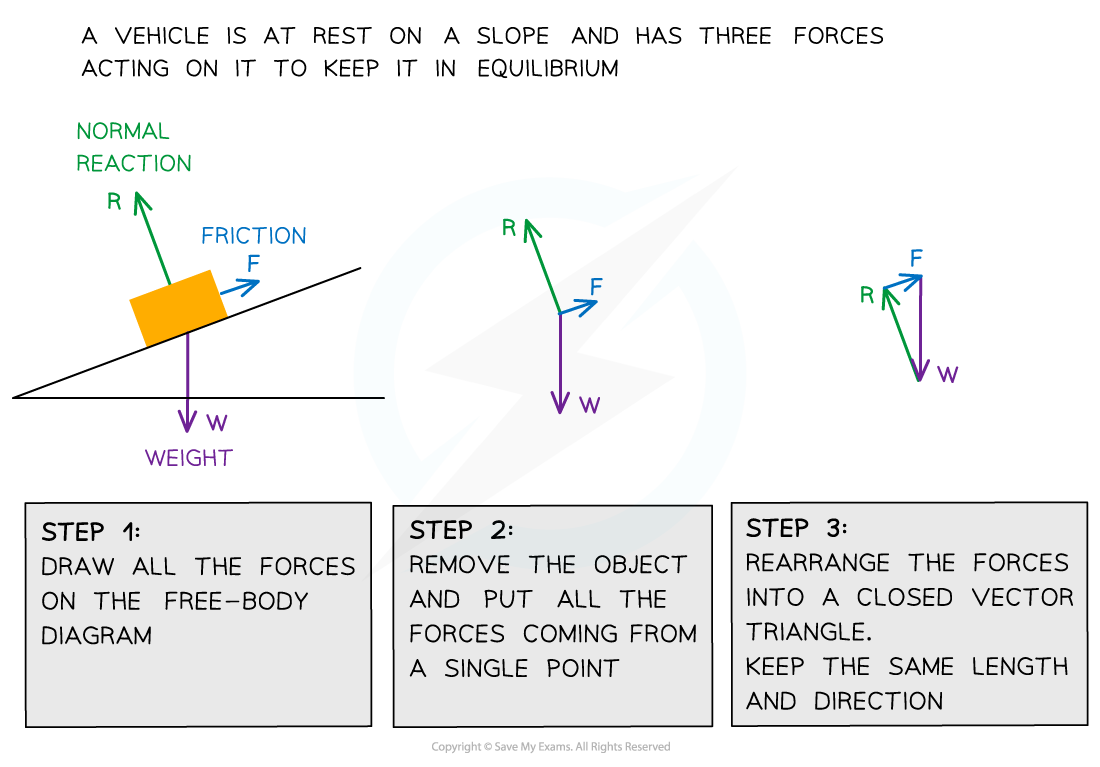
Three forces on an object in equilibrium form a closed vector triangle
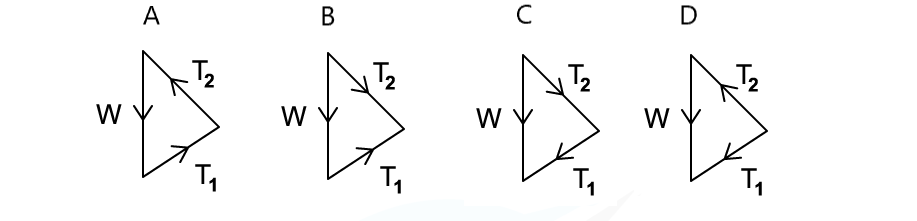
Worked Example
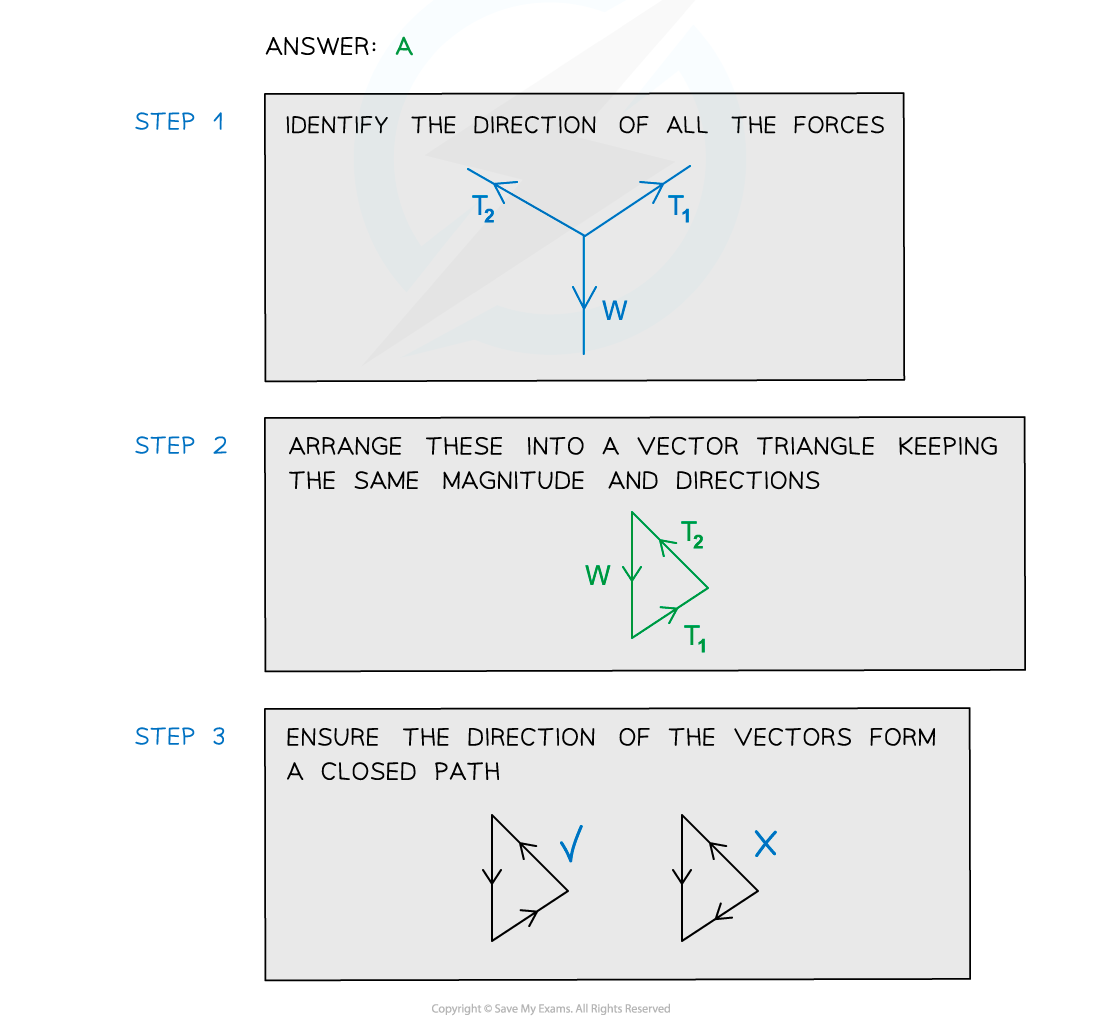
A weight hangs in equilibrium from a cable at point X. The tensions in the cables are T1 and T2 as shown.

Which diagram correctly represents the forces acting at point X?
Examiner Tips and Tricks
The diagrams in exam questions about this topic could ask you to draw to scale, so make sure you have a ruler handy!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
