Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesMechanics & MaterialsNewton’s Laws of MotionNewton's Second Law

Newton's Second Law (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Newton's Second Law

  • Newton's second law describes the change in motion that arises from a resultant force acting on an object

  • Newton's Second Law states that:

    The resultant force acting on an object with a constant mass is directly proportional to its acceleration

F space equals space m a

  • Where:

    • F = resultant force, measured in newtons (N)

    • m = mass of object, measured in kilograms (kg)

    • a = acceleration, measured in metres per second squared (m s−2)

  • This acceleration always acts in the same direction as the resultant force

  • When unbalanced forces act on an object, the object experiences a resultant force

  • If the resultant force acts along the direction of the object's motion, the object will:

    • Speed up (accelerate)

    • Slow down (decelerate)

  • If the resultant force acts on an object at an angle to its direction of motion, it will:

    • Change direction 

Resultant Force

  • Force is a vector quantity with both magnitude and direction

  • The resultant force is, therefore, the vector sum of all the forces acting on the body

  • If the object is in motion, then the positive direction is in the direction of motion

4-4-newtons-2nd-law-example-calcs

Resultant forces on a body can be positive or negative depending on their direction

  • If the resultant force acts at an angle to the direction of motion, the magnitude and direction of the resultant force can be found by

Acceleration

  • Acceleration is a vector quantity with both magnitude and direction

  • If the resultant force acts in the direction of an object's motion, the acceleration is positive

  • If the resultant force opposes the direction of the object's motion, the acceleration is negative 

  • But the acceleration will always act in the same direction as the resultant force

Examiner Tips and Tricks

It is important to understand that for an object in motion, a resultant force that opposes that motion will cause the object to decelerate, not to suddenly travel backwards. 

If no drag forces are present, then the acceleration of a falling object is independent of its mass. This unintuitive fact of physics has been proven by astronauts on the Moon, who simultaneously dropped both a hammer and a feather from equal heights and found that they hit the ground at the same time! (Because there is no air resistance on the Moon.)

Worked Example

A rocket produces an upward thrust of 15 MN and has a weight of 8 MN.

A.    When in flight, the force due to air resistance is 500 kN.

Determine the resultant force on the rocket.

B.     The mass of the rocket is 0.8 × 105 kg.

Calculate the acceleration of the rocket, and state the direction of the acceleration.

Answer

Part (a)

Step 1: Draw a force diagram of the situation

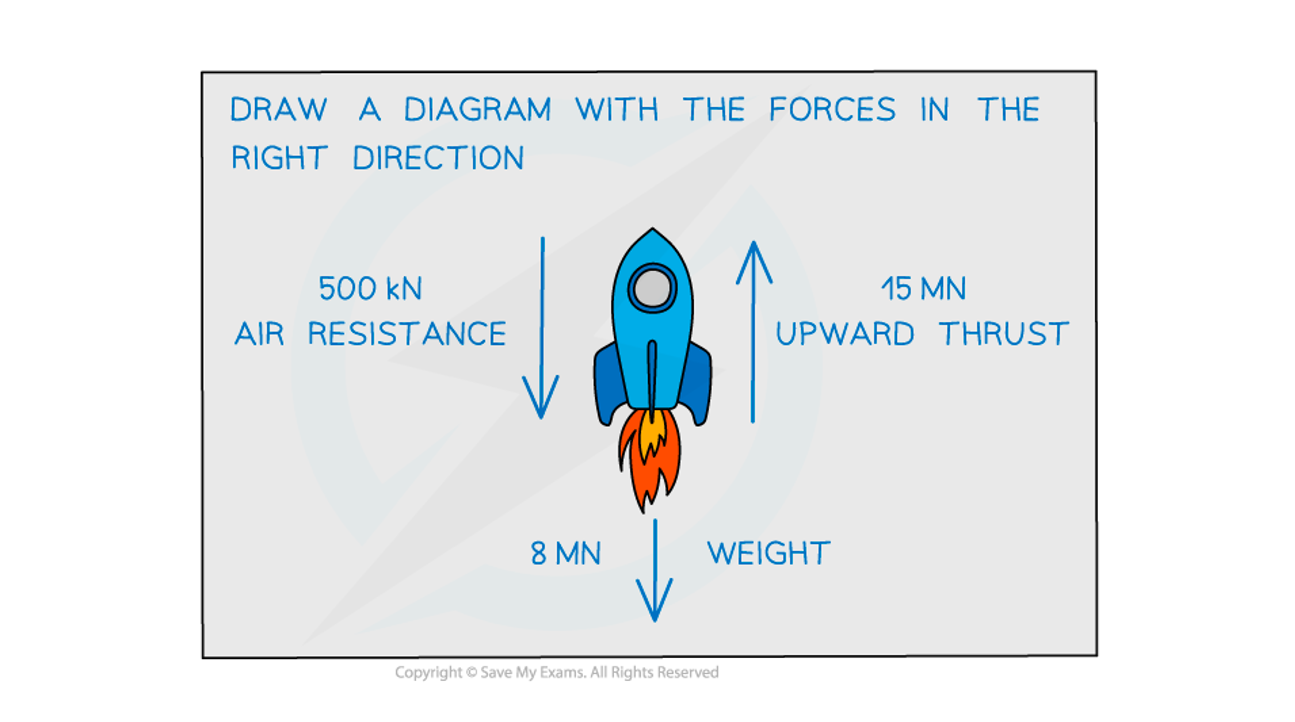
we---newtons-second-law-on-rocket-answer-image1

Step 2: Convert the forces into newtons and assign directions

  • The direction of motion is upwards, therefore upwards is the positive direction

    • Air resistance (downward acting) = −500 kN = −500 × 103 N

    • Weight (downward acting) = −8 MN = −8 × 106 N

    • Thrust (upward acting) = 15 MN = 15 × 106 N

Step 3: Calculate the resultant force

F space equals space open parentheses 15 cross times 10 to the power of 6 close parentheses space plus space open parentheses negative 8 cross times 10 to the power of 6 close parentheses space plus space open parentheses negative 500 cross times 10 cubed close parentheses

F space equals space 6.5 cross times 10 to the power of 6 space straight N space equals space 6.5 space MN

  • The positive value indicates that the resultant force acts in the direction of motion i.e., upwards

 

Part (b)

Step 1: State the equation for Newton's second law and rearrange to make acceleration the subject

F space equals space m a space space rightwards double arrow space space a space equals fraction numerator space F over denominator m end fraction

Step 2: Calculate the acceleration and state the direction

a space equals space fraction numerator 6.5 cross times 10 to the power of 6 over denominator 0.8 cross times 10 to the power of 5 end fraction

a space equals space 81 space straight m space straight s to the power of negative 2 end exponent space open parentheses 2 space straight s. straight f. close parentheses upwards

  • Acceleration is in the same direction as the resultant force

Examiner Tips and Tricks

It is a general rule to consider the direction of the object's motion as positive. Therefore, all vectors in the direction of motion will be positive, and opposing vectors, such as drag forces, will be negative. For stationary objects, you can choose which direction is positive or negative as long as you are consistent throughout your calculations. However, it is generally assumed that forward, upwards, and to the right are positive and backward, downwards, and to the left are negative.

Newton's Second Law and Momentum

  • Newton's second law can also be given in terms of momentum

    The resultant force on an object is equal to its rate of change of momentum

  • This change in momentum is in the same direction as the resultant force

  • These two definitions are derived from the definition of momentum, as follows:

  • Momentum:

 p space equals space m v

  • Rate of change of momentum:

 fraction numerator increment p over denominator increment t end fraction space equals space m fraction numerator increment v over denominator increment t end fraction

  • Force:

 F space equals space m fraction numerator increment v over denominator increment t end fraction

  • Acceleration:

 a space equals space fraction numerator increment v over denominator increment t end fraction

  • Therefore:

F space equals space m a 

Worked Example

A girl is riding her skateboard down the road and increases her speed from 1 m s-1 to 4 m s-1 in 2.5 s.

The force driving her forward is 72 N.

Calculate the combined mass of the girl and the skateboard.

WE - Newtons second law question image, downloadable AS & A Level Physics revision notes

Answer:

WE - Newtons second law answer image, downloadable AS & A Level Physics revision notes

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Newton’s First LawNext:Newton's Third Law
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.