Scalars & Vectors (AQA A Level Physics) : Revision Note
Did this video help you?
Scalars & Vectors
All quantities can be one of two types:
a scalar
a vector
Scalars
Scalars are quantities that have magnitude but not direction
For example, mass is a scalar quantity because it has magnitude but no direction
Vectors
Vectors are quantities that have both magnitude and direction
For example, weight is a vector quantity because it is a force and has both magnitude and direction
Distance and displacement
Distance is a measure of how far an object has travelled, regardless of direction
Distance is the total length of the path taken
Distance, therefore, has a magnitude but no direction
So, distance is a scalar quantity
Displacement is a measure of how far it is between two points in space, including the direction
Displacement is the length and direction of a straight line drawn from the starting point to the finishing point
Displacement, therefore, has a magnitude and a direction
So, displacement is a vector quantity
What is the difference between distance and displacement?
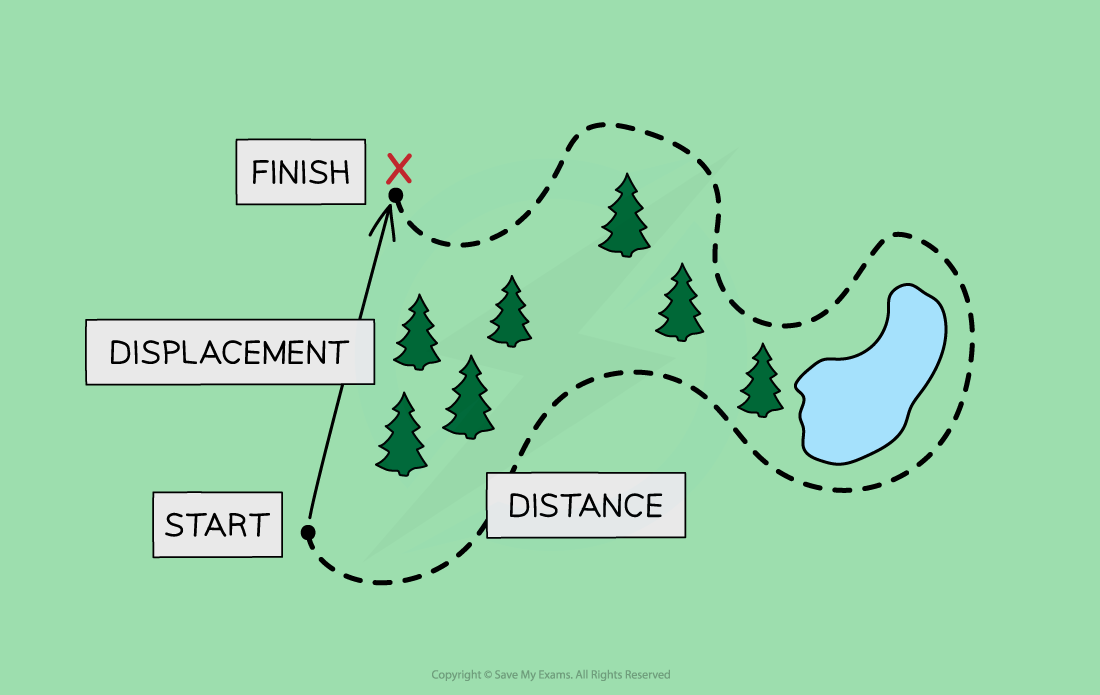
Displacement is a vector quantity while distance is a scalar quantity
When a student travels to school, there will probably be a difference in the distance they travel and their displacement
The overall distance they travel includes the total lengths of all the roads, including any twists and turns
The overall displacement of the student would be a straight line between their home and school, regardless of any obstacles, such as buildings, lakes or motorways, along the way
Speed and velocity
Speed is a measure of the distance travelled by an object per unit time, regardless of the direction
The speed of an object describes how fast it is moving, but not the direction it is travelling in
Speed, therefore, has magnitude but no direction
So, speed is a scalar quantity
Velocity is a measure of the displacement of an object per unit time, including the direction
The velocity of an object describes how fast it is moving and which direction it is travelling in
An object can have a constant speed but a changing velocity if the object is changing direction
Velocity, therefore, has magnitude and direction
So, velocity is a vector quantity
Examples of scalars & vectors
The table below lists some common examples of scalar and vector quantities
Table of scalars and vectors
Scalars | Vectors |
|---|---|
distance | displacement |
speed | velocity |
mass | acceleration |
time | force |
energy | momentum |
volume |
|
density |
|
pressure |
|
electric charge |
|
temperature |
|
Combining Vectors
Vectors are represented by an arrow
The arrowhead indicates the direction of the vector
The length of the arrow represents the magnitude
Vectors can be combined by adding them to produce the resultant vector
The resultant vector is sometimes known as the ‘net’ vector (eg. the net force)
There are two methods that can be used to add vectors
Calculation – if the vectors are perpendicular
Scale drawing – if the vectors are not perpendicular
Vector Calculation
Vector calculations will be limited to two vectors at right angles
This means the combined vectors produce a right-angled triangle and the magnitude (length) of the resultant vector is found using Pythagoras’ theorem
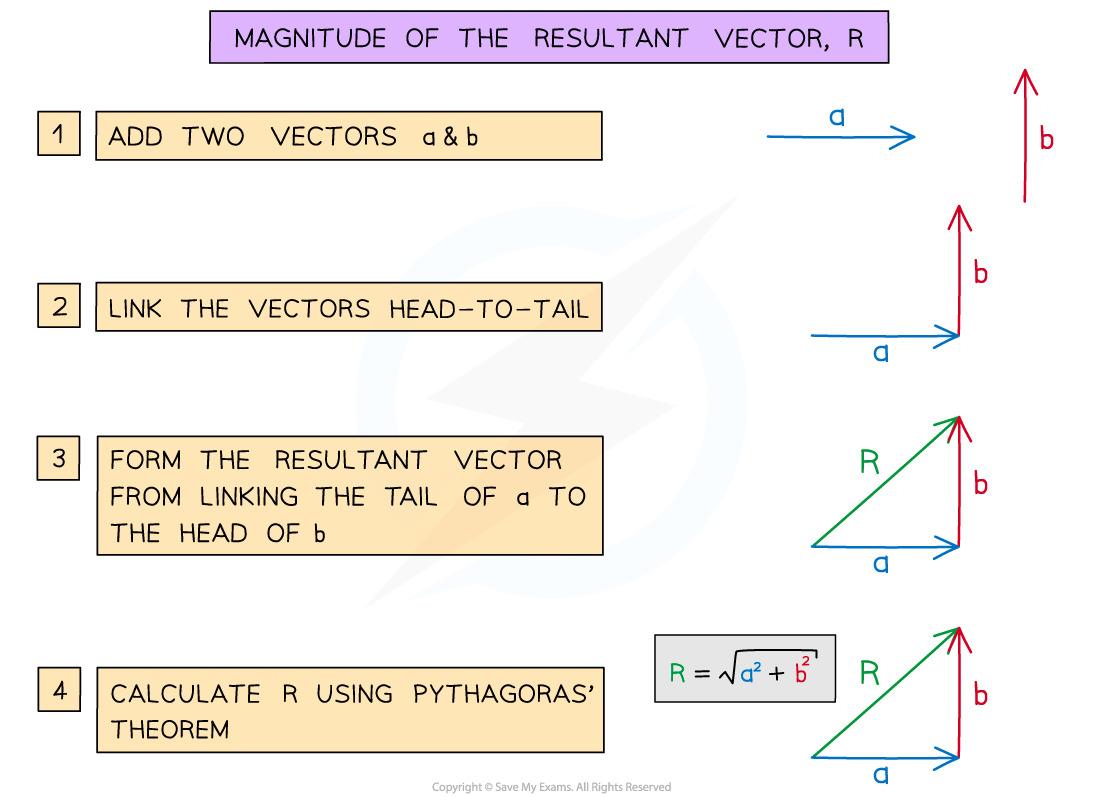
The magnitude of the resultant vector is found by using Pythagoras’ Theorem
The direction of the resultant vector is found from the angle it makes with the horizontal or vertical
The question should imply which angle it is referring to (ie. Calculate the angle from the x-axis)
Calculating the angle of this resultant vector from the horizontal or vertical can be done using trigonometry
Either the sine, cosine or tangent formula can be used depending on which vector magnitudes are calculated

The direction of vectors is found by using trigonometry
Scale Drawing
When two vectors are not at right angles, the resultant vector can be calculated using a scale drawing
Step 1: Link the vectors head-to-tail if they aren’t already
Step 2: Draw the resultant vector using the triangle or parallelogram method
Step 3: Measure the length of the resultant vector using a ruler
Step 4: Measure the angle of the resultant vector (from North if it is a bearing) using a protractor
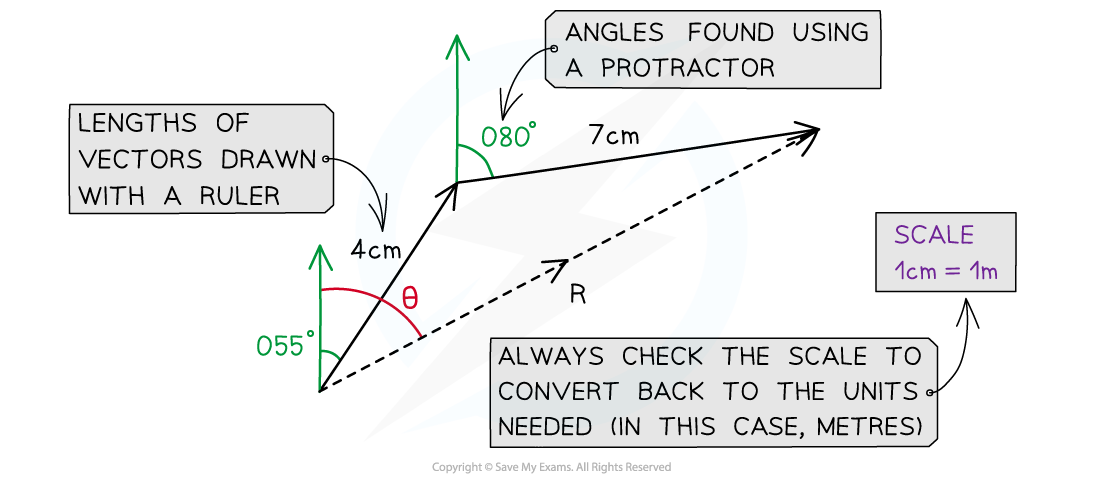
A scale drawing of two vector additions. The magnitude of resultant vector R is found using a rule and its direction is found using a protractor
Note that with scale drawings, a scale may be given for the diagram such as 1 cm = 1 km since only limited lengths can be measured using a ruler
The final answer is always converted back to the units needed in the diagram
Eg. For a scale of 1 cm = 2 km, a resultant vector with a length of 5 cm measured on your ruler is actually 10 km in the scenario
There are two methods that can be used to combine vectors: the triangle method and the parallelogram method
To combine vectors using the triangle method:
Step 1: link the vectors head-to-tail
Step 2: the resultant vector is formed by connecting the tail of the first vector to the head of the second vector
To combine vectors using the parallelogram method:
Step 1: link the vectors tail-to-tail
Step 2: complete the resulting parallelogram
Step 3: the resultant vector is the diagonal of the parallelogram
Vector Addition

Vector Subtraction

Worked Example
A hiker walks a distance of 6 km due east and 10 km due north. Calculate the magnitude of their displacement and its direction from the horizontal
Answer:

Examiner Tips and Tricks
Pythagoras' Theorem and trigonometry are consistently used in vector addition, so make sure you're fully confident with the maths here!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
