Refractive Index
- The refractive index of a material is the ratio of how fast light travels through that particular substance compared to the speed of light in a vacuum
Refraction
-
Refraction is:
The change in direction of a wave when it passes through a boundary between mediums of different density
- This change of direction is caused by a change in the speed of different parts of the wavefront as they hit the boundary
- In optics, the word medium is used to describe a transparent material
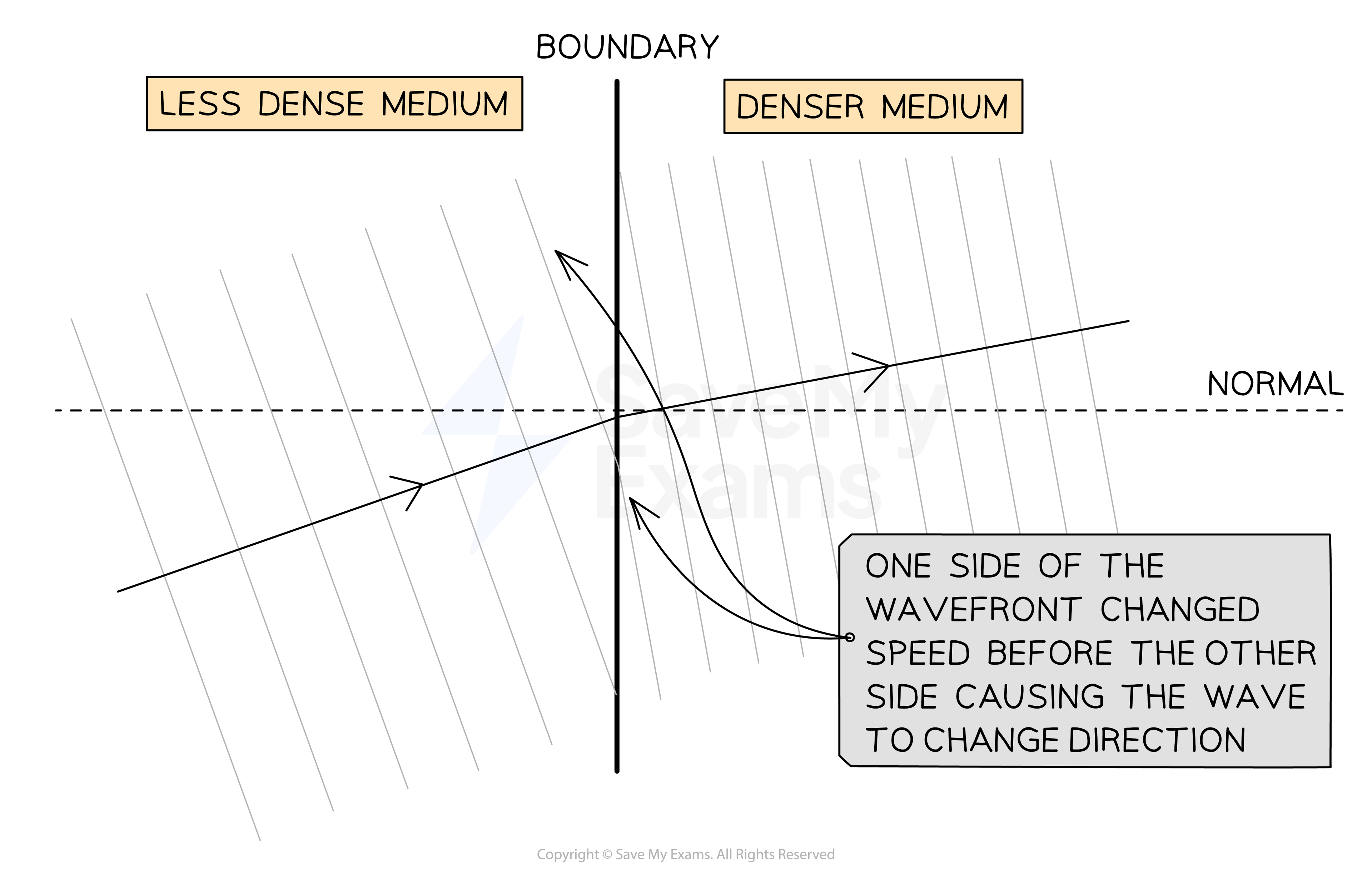
A wavefront changes direction when part of it hits a boundary and changes speed before the other parts
Conditions for refraction
- The more optically dense the medium, the slower the waves travel and the smaller the angle of refraction
- The light bends towards the normal
- The less optically dense the medium, the faster the waves travel and the larger the angle of refraction
- The light bends away from the normal
- The amount of refraction that takes place is determined by the difference between the angles of incidence (i) and refraction (r) of the waves at the boundary
- The angles of incidence and refraction are measured from the normal line
- This is drawn at 90° to the boundary between the two media
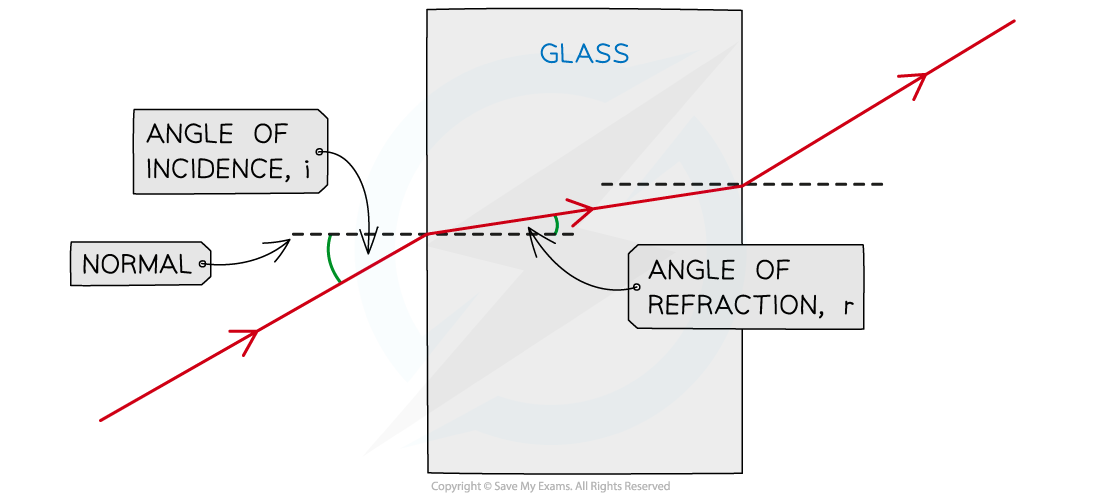
The angle of incidence is the angle between the approaching incident ray and the normal. The angle of refraction is the angle between the ray leaving the boundary and the normal.
-
The amount of change in direction that takes place depends on the difference in optical density between the two media
- When light passes from a less dense medium to a more dense medium, (e.g. air → glass):
- The refracted light has a lower speed and a shorter wavelength than the incident light
- When light passes from a more dense medium to a less dense medium (e.g. glass → air):
- The refracted light has a higher speed and a longer wavelength than the incident light
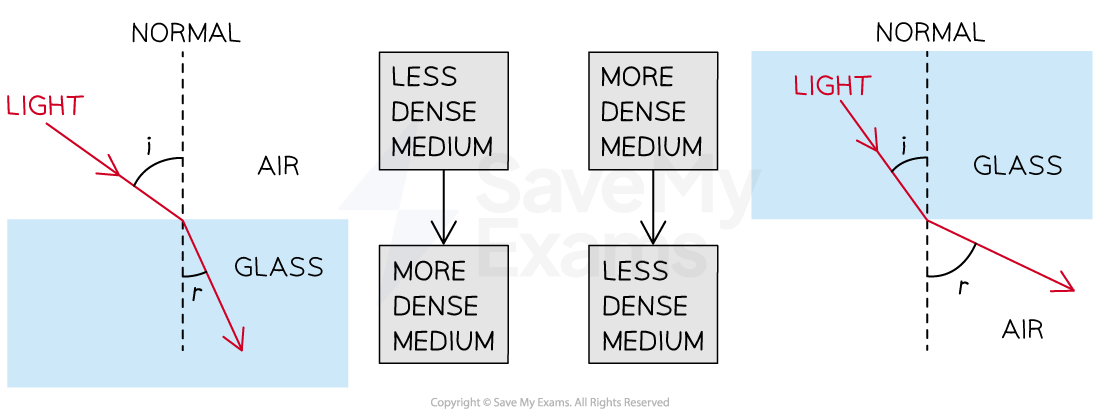
When light passes from a less to a more dense material the ray refracts towards the normal
- When a wave refracts, its speed and wavelength change, but its frequency remains the same
- This is noticeable by the fact that the colour of the wave does not change
- When the light ray is incident on the boundary at 90°:
- The wave passes straight through without direction
- This is because the whole wavefront enters the boundary at the same time
Light travelling along the normal to the boundary between material 1 and material 2
Refractive Index
- The refractive index, n of a material tells us how optically dense it is
- The refractive index of air is n = 1
- Media that are more optically dense than air will have a refractive index of n > 1
- Media that are less optically dense than air will have a refractive index of n < 1
The higher the refractive index of a material then the more optically dense and hence the slower light will travel through it
- The refractive index of a material is calculated using the equation:
-
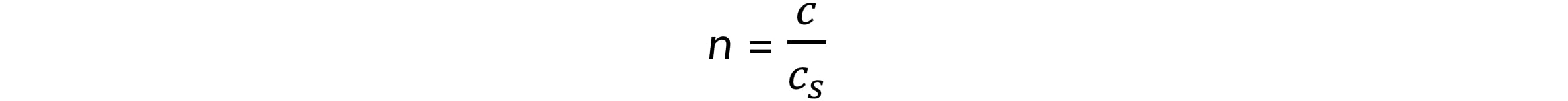
- Where:
- n = refractive index of material
- c = the speed of light in a vacuum (m s–1)
- cs = the speed of light in a substance (m s–1)
- Where:
- Note that, being a ratio, the absolute refractive index is a dimensionless quantity
- This means that it has no units
Examiner Tip
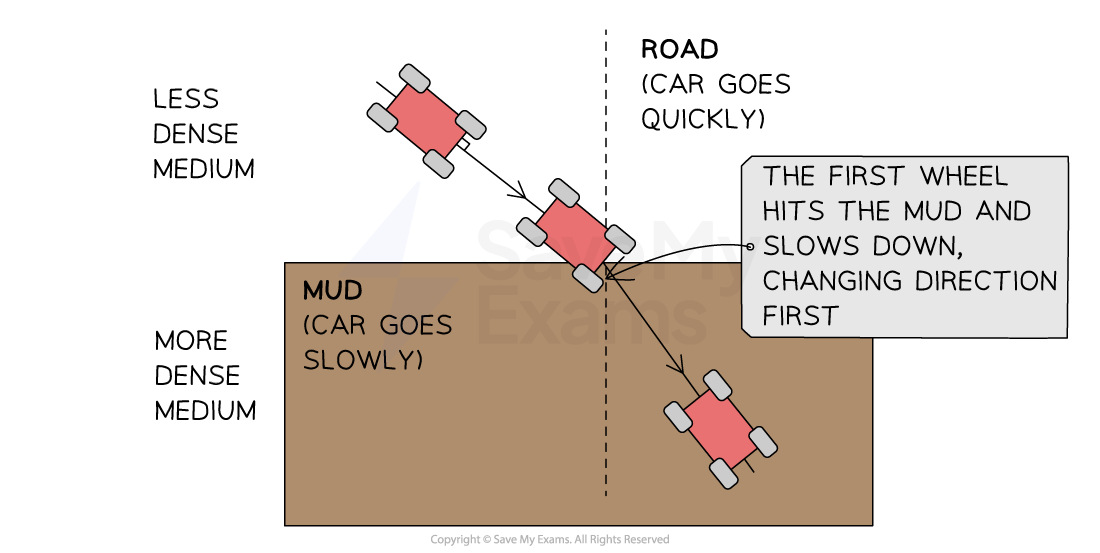
It can be tricky to understand the concept of refraction. Imagine a car driving at an angle from a road and onto a patch of mud. The wheel that hits the mud will slow down first whilst the second wheel continues to travel at the initial speed. This causes the car to turn. 
Always double-check if your calculations for the refractive index are greater than 1. Otherwise, something has gone wrong in your calculation! The refractive index of air will not be given in the question. Always assume that nair = 1. The refractive index of air is often written as n or n1 when solving questions.
