Single Slit Diffraction (AQA A Level Physics)

• Diffraction is:

the spreading out of waves after they pass through a narrow gap or around an obstruction

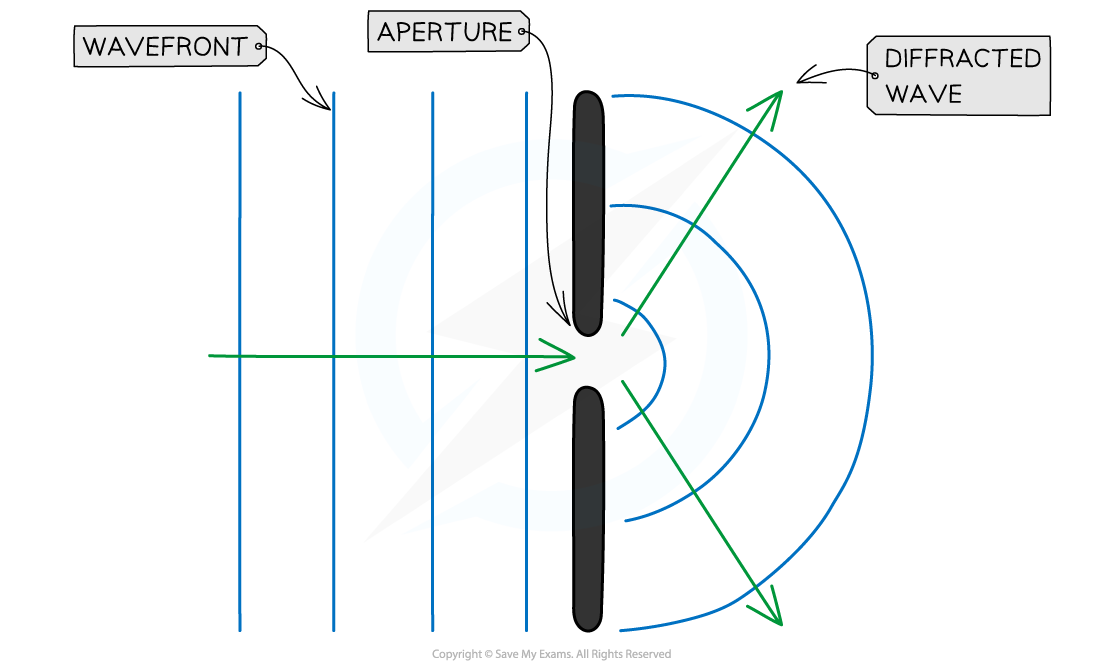
Diffraction: after passing through a narrow gap, the waves curve as they spread out

• The extent of their diffraction depends on the width of the gap compared to the wavelength of the waves

• For gaps that are much much smaller than the wavelength of the wave, no diffraction occurs

• For gaps that are much much bigger than the wavelength of the wave, no diffraction occurs

• When the wavelength of the wave and the width of the gap are similar in size, then diffraction occurs:
  • When the wavelength is bigger than the gap, more diffraction occurs,
    • The wave spreads out more after passing through
  • When the wavelength is smaller than the gap, less diffraction occurs
    • The wave spreads out less after passing through
•  After passing through a gap:
  • The waves spread out so they have curvature 
  • The amplitude of the wave is less because the barrier on either side of the gap absorbs wave energy

• The wavefronts of the wave represent the crests and troughs

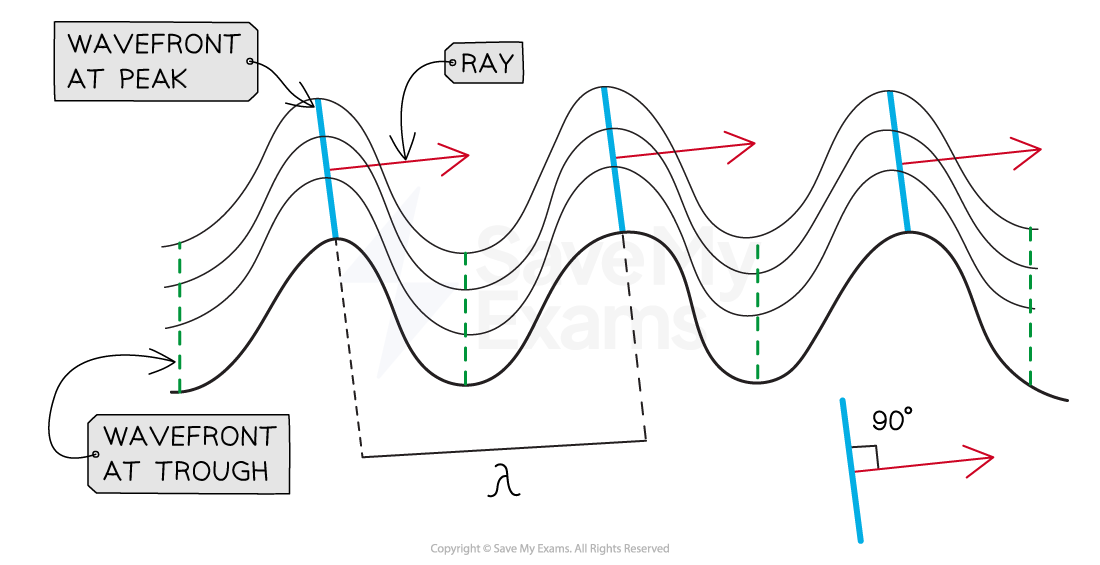
Wavefronts and rays for transverse waves travelling in a horizontal plane

• The only property of a wave that changes when it diffracts is its amplitude
  • The wavelength of the wave remains the same

• Examples of diffraction include:
  • Radio waves moving in between or around buildings
  • Water waves moving through a gap into a harbour

Waves diffract through a gap in a barrier in a harbour

Single Slit Monochromatic Diffraction Pattern

• The diffraction pattern of light passing through a single slit is a series of light and dark fringes on a screen
  
  • The bright fringes are areas of maximum intensity, produced by the constructive interference of each part of the wavefront as it passes through the slit
  • The dark fringes are areas of zero or minimum intensity, produced by the destructive interference of each part of the wavefront as it passes through the slit

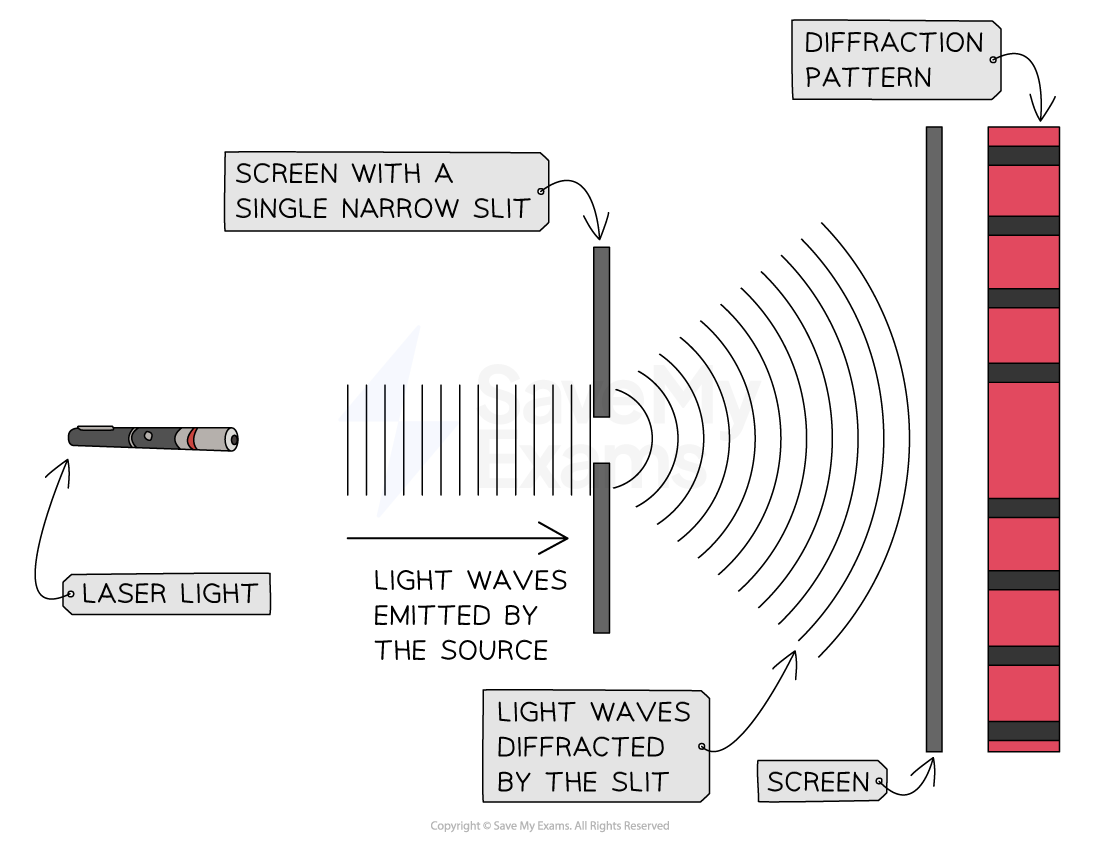
The diffraction pattern produced by a laser beam diffracted through a single slit onto a screen is different to the diffraction pattern produced through a double slit

• The central maximum is:
  • Much wider and brighter than the other bright fringes
  • Much wider than that of the double-slit diffraction pattern
• On either side of the wide central maxima are much narrower and less bright maxima
  • These get dimmer as the order increases

Single Slit Monochromatic Intensity Pattern

• If a laser emitting blue light is directed at a single slit, where the slit width is similar in size to the wavelength of the light, its intensity pattern will be as follows:

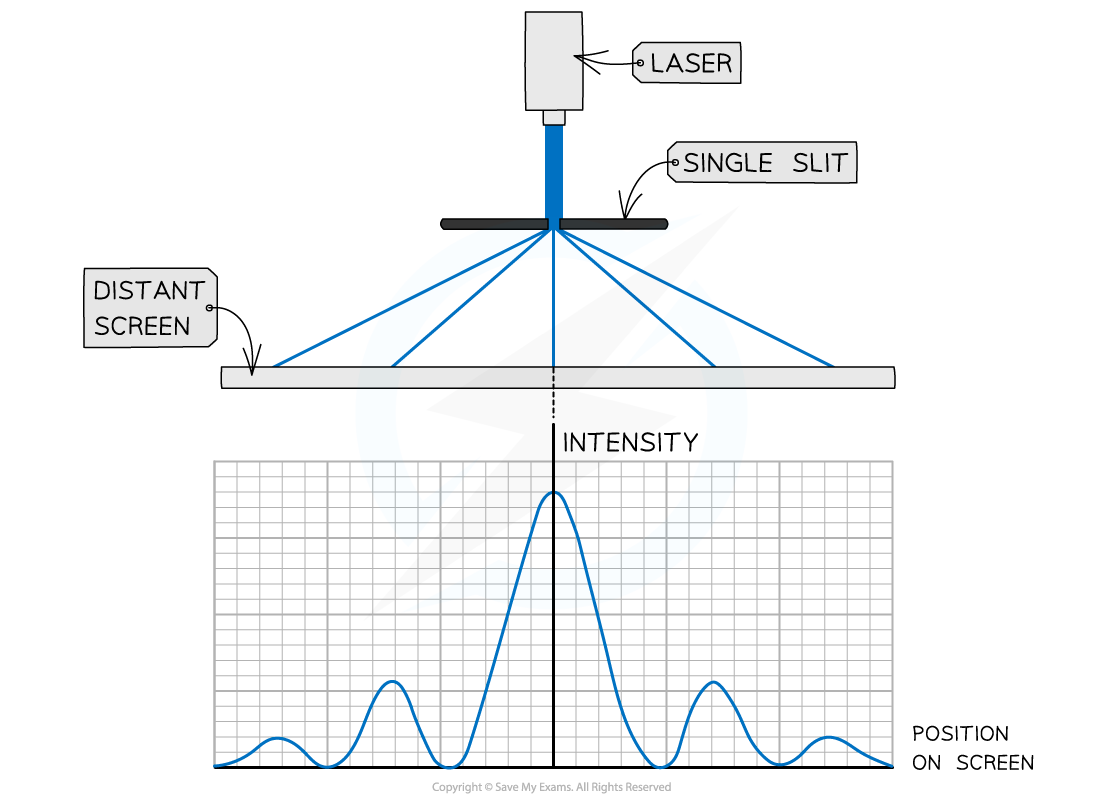
The intensity pattern of blue laser light diffracted through a single slit

• The features of the single slit intensity pattern are: 
  • The central bright fringe has the greatest intensity of any fringe and is called the central maximum
  • The dark fringes are regions with zero intensity
  • Moving away from the central maxima either side, the intensity of each bright fringe gets less

Single Slit Diffraction and Intensity Patterns of White Light

• A source of white light diffracted through a single slit will produce the following diffraction pattern:
  • It is different to that produced by a double slit or a diffraction grating
• The central maximum is bright white because constructive interference from all the colours happens here:
  • Much wider and brighter than the other bright fringes
  • Much wider than that of the double-slit diffraction pattern
• All other maxima are composed of a spectrum
• Separate diffraction patterns can be observed for each wavelength of light
  • The shortest wavelength (violet / blue) would appear nearest to the central maximum because it is diffracted less
  • The longest wavelength (red) would appear furthest from the central maximum because it is diffracted more
• The colours look blurry and further away from the central maximum, the fringe spacing gets so small that the spectra eventually merge without any space between them
  • As the maxima move further away from the central maximum, the wavelengths of blue observed decrease and the wavelengths of red observed increase

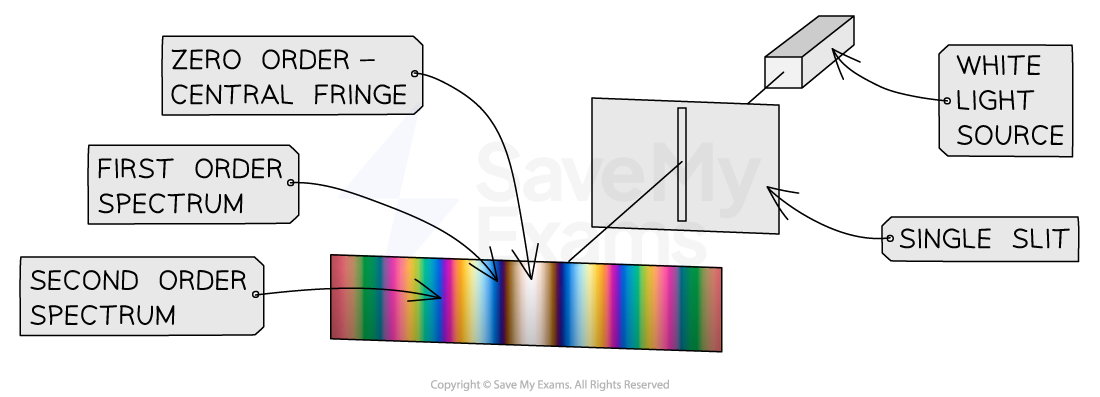
The diffraction pattern of white light diffracted through a single slit

• A source of white light diffracted through a single slit will produce the following intensity pattern:
  • The central maxima is equal in intensity to that of monochromatic light
  • The non-central maxima are wider and less intense
  • The fringe spacing between the maxima get smaller
  • The amount of red wavelengths in the pattern increases with increasing maxima, n increases from n = 1, 2, 3...
  • The amount of blue wavelengths decrease with increasing maxima

The intensity pattern for the diffraction of white light through a single slit

• As discussed above, the effects of diffraction are most prominent when the gap size is approximately the same as the wavelength of the wave
  • As the gap size increases, compared to the wavelength, the waves spread out less after they pass through the gap

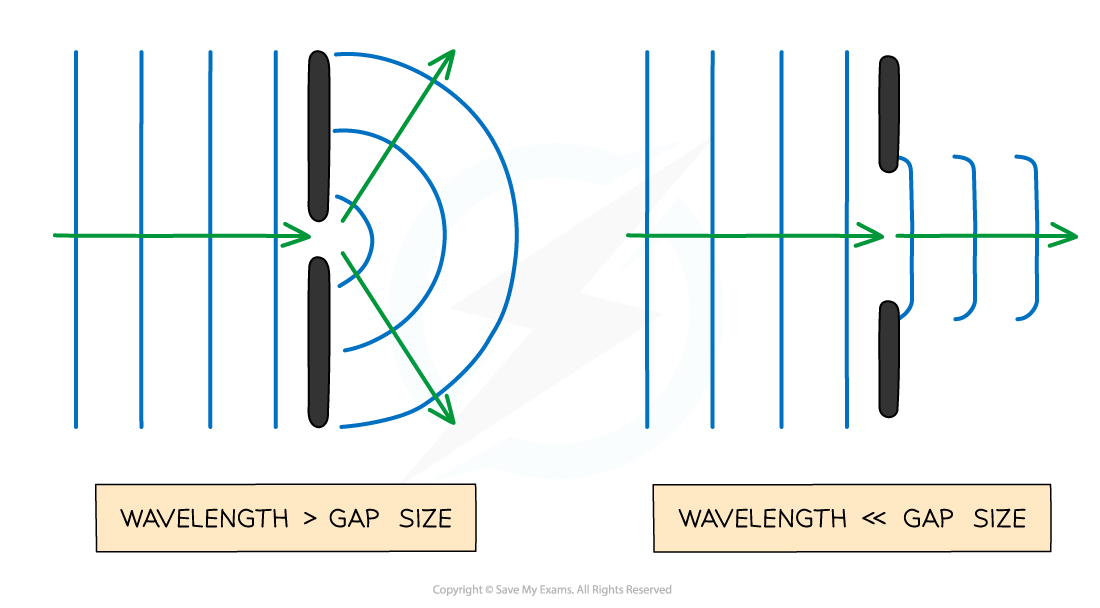
The size of the gap (compared to the wavelength) affects how much the waves spread out when diffracted through a gap

Changes in Wavelength

• When the wavelength passing through the gap is increased then the wave diffracts more
• This increases the angle of diffraction of the waves as they pass through the slit
  • So the width of the bright maxima is also increased
• Red light – which has the longest wavelength of visible light – will produce a diffraction pattern with wide fringes
• Blue light – which has a much shorter wavelength – will produce a diffraction pattern with narrow fringes

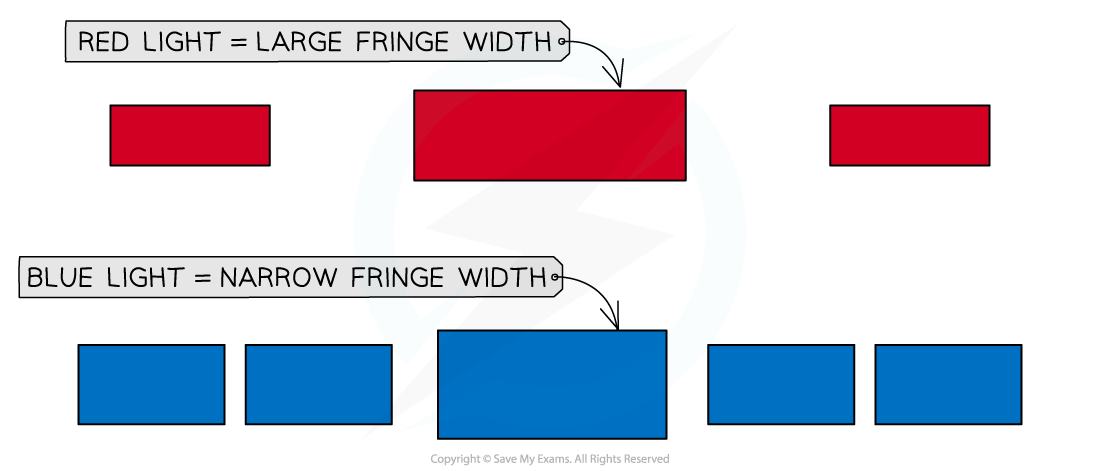
Fringe width depends on the wavelength of the light 

• If the blue laser is replaced with a red laser:
  • There is more diffraction as the waves pass through the single slit
  • So the fringes in the intensity pattern would therefore be wider

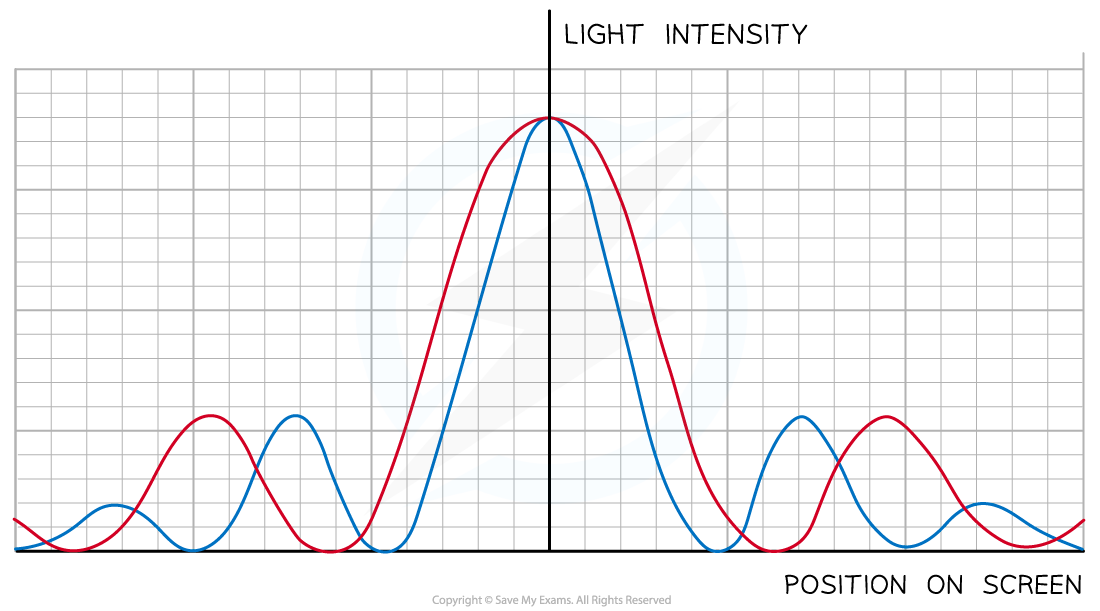
The intensity pattern of red laser light shows longer wavelengths diffract more than shorter wavelengths

Changes in Slit Width

• If the slit was made narrower:
  • The angle of diffraction is greater
  • So, the waves spread out more beyond the slit
• The intensity graph will show that: 
  • The intensity of the maxima decreases
  • The width of the central maxima increases
  • The spacing between fringes is wider

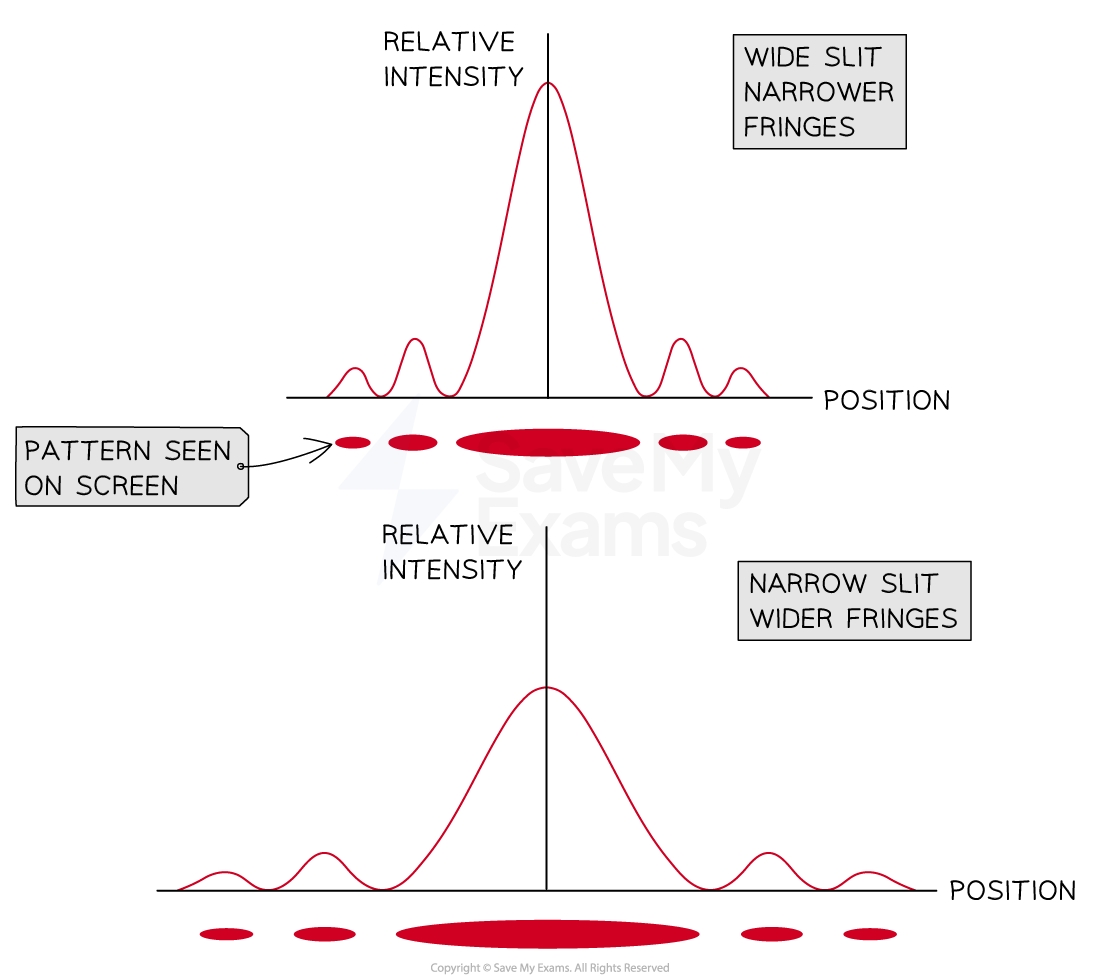
When the slits are made wider then the fringes become narrower and vice versa

     ANSWER:   D

• Diffraction is most prominent when the wavelength is close to the aperture size
• UV waves have a wavelength between 4 × 10^–7 – 1 × 10^–8 m so won’t be diffracted by a gate post
• Sound waves have a wavelength of 1.72 × 10^–2 – 17 m so would not be diffracted by the diffraction grating
• Radio waves have a wavelength of 0.1 – 10⁶ m so would not be diffracted by human hair
• X-rays have a wavelength of 1 × 10^–8 – 4 × 10^–13 m which is roughly the gap between atoms in a crystalline solid
  • Therefore, the correct answer is D