Demonstrating Interference (AQA A Level Physics): Revision Note

Interference & Diffraction of a Laser

• Lasers are the ideal piece of equipment to analyse diffraction and intensity patterns because they form light that is:

  • Coherent (have a constant phase difference and frequency)

  • Monochromatic (have the same wavelength)

A laser produces a beam of coherent monochromatic light

• The diffraction pattern produced by a laser on a screen is made up of:

  • Areas of constructive interference - the bright strips or fringes

  • Areas of destructive interference - the dark fringes

Laser diffraction patterns produced by gratings with different numbers of slits

• Other sources of light, such as a filament bulb or a sodium lamp, are non-coherent, so they produce white light

Safety Issues with Lasers

• Lasers produce a very high-energy beam of light

• This intense beam can cause permanent eye damage or even blindness

Precautions

• It's important to use lasers safely and follow the guidelines:

  • Never look directly at a laser or its reflection

  • Don’t shine the laser towards a person

  • Don't allow a laser beam to reflect from shiny surfaces into someone else's eyes

  • Wear laser safety goggles

  • Place a ‘laser on’ warning light outside the room

  • Stand behind the laser

Placing a laser warning sign outside of the door is one precaution that can be taken when using lasers

Sound & EM Wave Interference

Using Sound Waves

• Two-source interference can be demonstrated with two speakers emitting a coherent sound

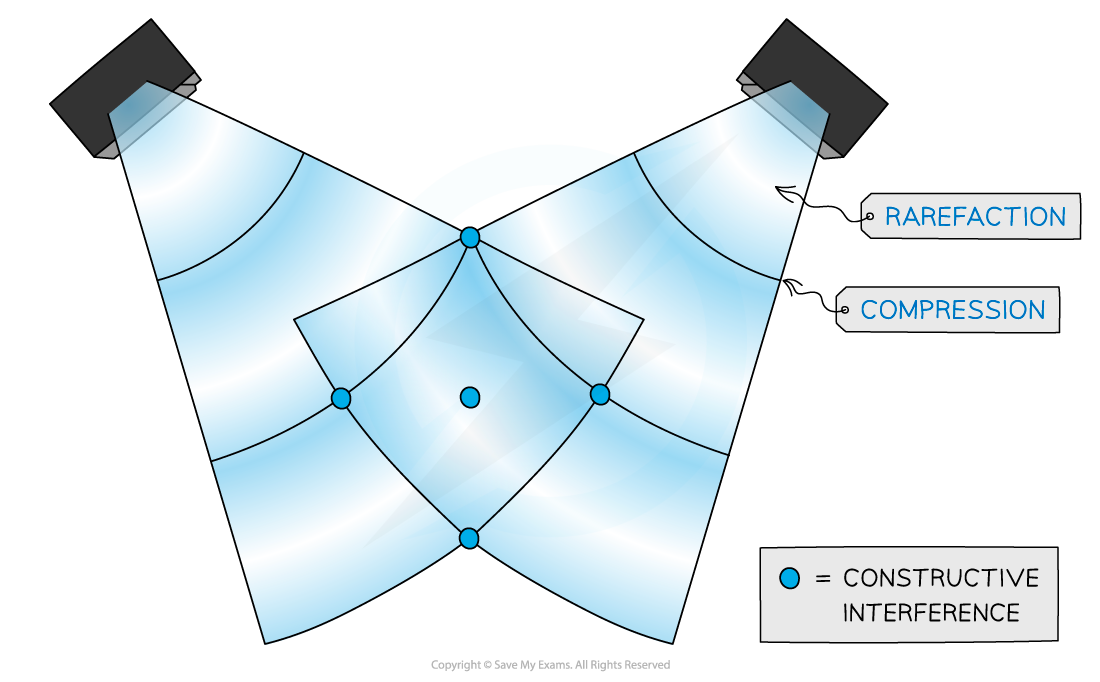
Sound wave interference from two speakers emitting a coherent sound

• Sound waves are longitudinal waves made up of compressions and rarefactions

  • Constructive interference occurs when the compressions and rarefactions from each wave line up and the sound appears louder

  • Destructive interference occurs when a compression from one wave lines up with a rarefaction from the other and vice versa. The two waves cancel each other out, so zero sound is heard. 

  • This is the technology used in noise-cancelling headphones

Using Microwaves

• Two-source interference for microwaves (and other electromagnetic waves) can be detected with a moveable microwave detector

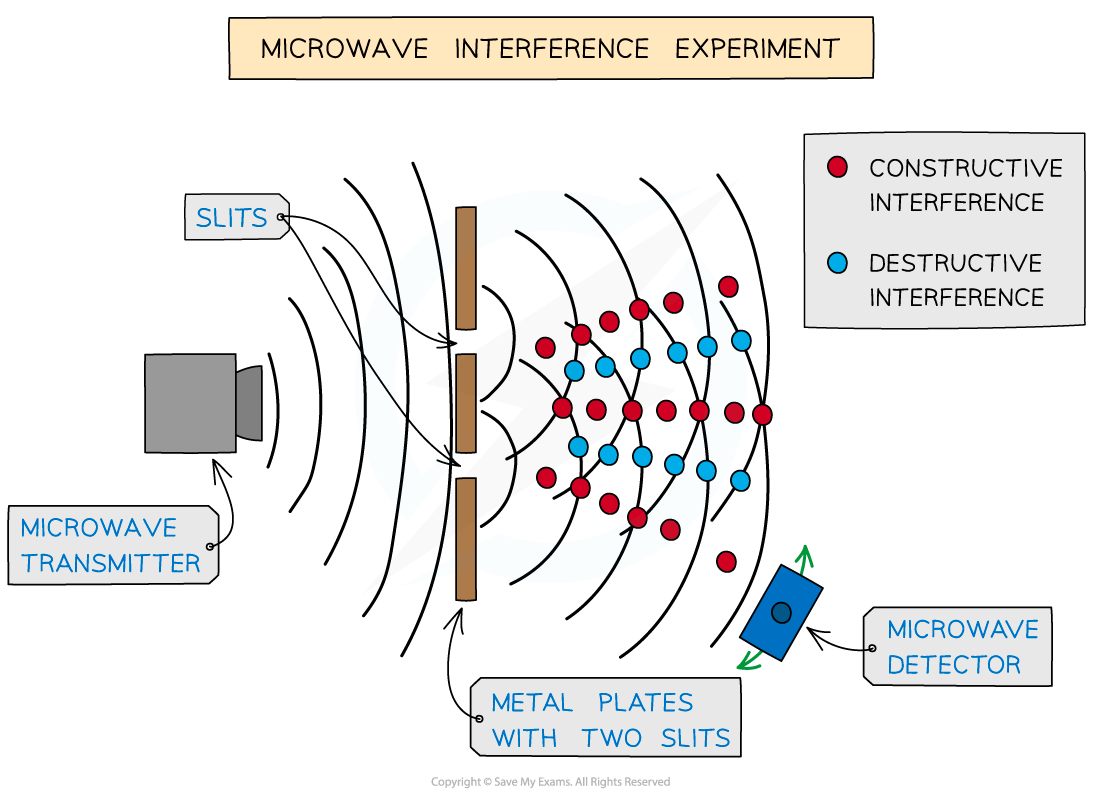
A microwave interference experiment creates a diffraction pattern the same as that of a laser beam

• The detector picks up a maximum amplitude or intensity in regions of constructive interference 

• The detector picks up a minimum or zero amplitude, so no signal in regions of destructive interference 

Intensity Variation with Amplitude

• By definition, the intensity of a wave (its power per unit area) is proportional to the energy transferred by the wave

• The intensity of a wave at a particular point is related to the amplitude of the wave at that point

• The energy transferred by a wave is proportional to the square of the amplitude

• Therefore, the intensity of a wave is proportional to the square of the amplitude 

• Where:

  • I = intensity of the wave in W m^–2

  • A = amplitude of the wave in metres (m)