Application of Conservation Laws (AQA A Level Physics): Revision Note
Exam code: 7408
Application of Conservation Laws
All particle interactions must obey a set of conservation laws. These are conservation of:
Charge, Q
Baryon number, B
Lepton Number, L
Strangeness, S
Energy (or mass-energy)
Momentum
However, strangeness does not need to be conserved in weak interactions. It can change by either 0, +1 or –1
Quantum numbers such as Q, B, L and S can only take discrete values (ie. 0, +1, –1, 1/2)
To know whether a particle interaction can occur, check whether each quantum number is equal on both sides of the equation
If even one of them, apart from strangeness in weak interactions, is not conserved then the interaction cannot occur
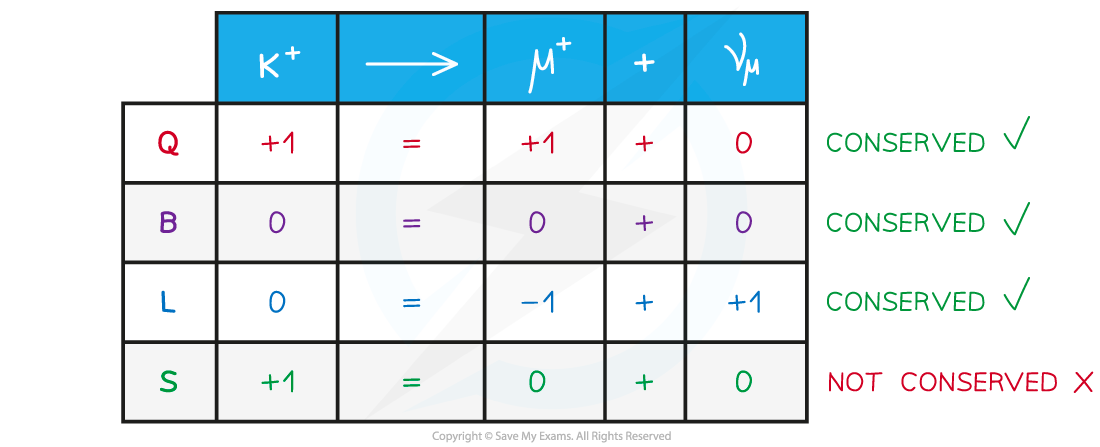
Example of a working out what is conserved in Kaon decay. This decay must be through the weak interaction since S is not conserved
Worked Example
The lambda nought particle Λ0 is made up from the quarks uds. Show, in terms of the conservation of charge, strangeness, baryon number and lepton number whether the following interaction is permitted
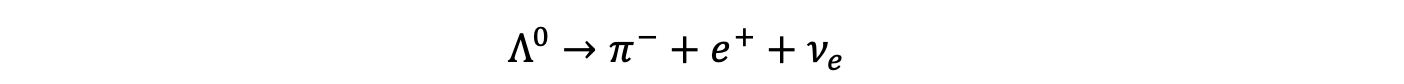
Answer:
Step 1: Determine conservation of charge
0 = –1 + 1 + 0
Charge is conserved
Step 2: Determine conservation of strangeness
Λ0 has an s quark, so must have a strangeness of –1
–1 = 0 + 0 + 0
Strangeness is not conserved
Step 3: Determine conservation of baryon number
Λ0 is a baryon since it has 3 quarks, so must have a baryon number of +1
+1 = 0 + 0 + 0
Baryon number is not conserved
Step 4: Determine conservation of lepton number
Λ0 is a baryon, so must have a lepton number of 0
0 = 0 + (–1) + 1
Lepton number is conserved
Step 5: Conclusion
Since the baryon number is not conserved, this interaction is not permitted
Worked Example
The equation for β– decay is
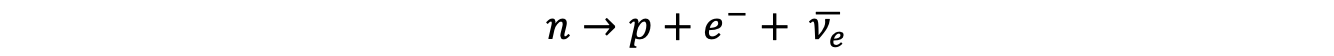
Using the quark model of beta decay, prove that the charge is conserved in this equation.
Answer:

Examiner Tips and Tricks
Note:
Quantum numbers for any exotic particles will be given in the question
All the rest can be found on the datasheet or can be deduced using the information provided

Unlock more, it's free!
Did this page help you?