Leptons (AQA A Level Physics): Revision Note
Exam code: 7408
Leptons & Antileptons
Leptons are a group of fundamental (elementary) particles
This means they are not made up of any other particles (no quarks)
Leptons interact with other particles via the weak, gravitational or electromagnetic interactions
They do not interact via the strong nuclear force
The most common leptons are:
The electron, e–
The electron neutrino, ve
The muon, μ–
The muon neutrino, vμ
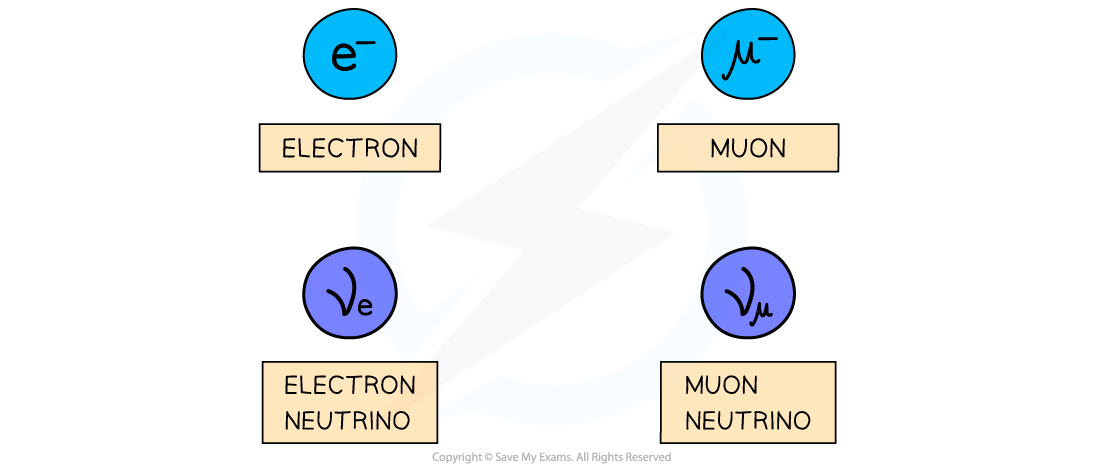
The most common leptons are the electron, muon and their respective neutrinos
The muon is similar to the electron but is slightly heavier
The mass of an electron is about 0.0005u, whereas the mass of a muon is about 0.1u
Electrons and muons both have a charge of -1e
Neutrinos are the most abundant leptons in the universe and have no charge and negligible mass (almost 0)
Although quarks are fundamental particles too, they are not classed as leptons
Leptons do not interact with the strong force, whilst quarks do
Worked Example
Circle all the anti-leptons in the following decay equation.
Answer:

Lepton Number
Similar to baryon number, the lepton number, L is the number of leptons in an interaction
L depends on whether the particle is a lepton, anti-lepton or neither
Leptons have a lepton number L = +1
Anti-leptons have a lepton number L = –1
Particles that are not leptons have a lepton number L = 0
Lepton number is a quantum number and is conserved in all interactions
This is helpful for knowing whether an interaction is able to happen
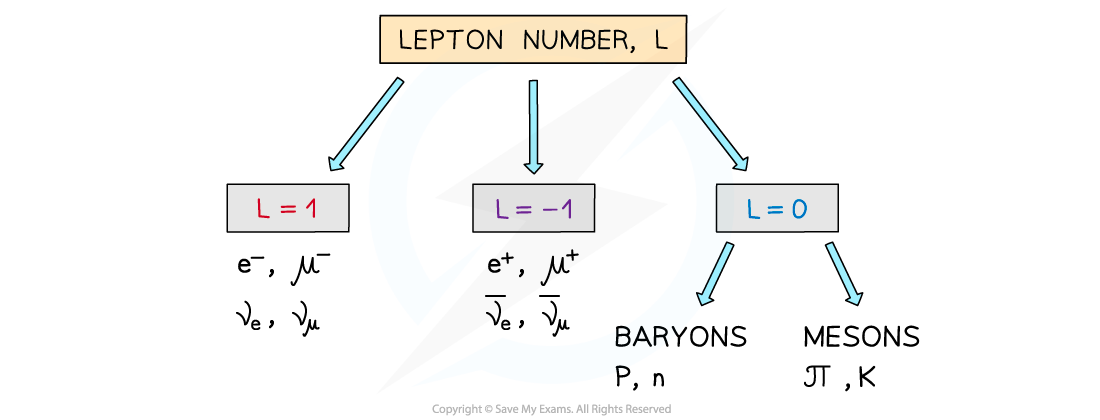
The lepton number depends if the particle is a lepton, anti-lepton or neither
Worked Example
If the lepton number is conserved in the following decay, identify whether particle X should be a neutrino or anti-neutrino
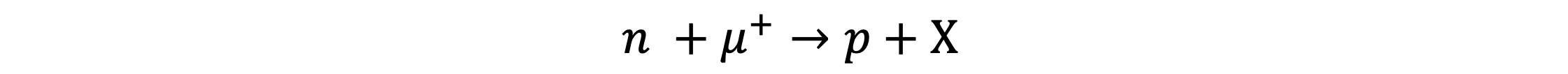
Answer:
Step 1: Determine the lepton number of all the particles on both sides of the equation
0 + (–1) = 0 + X
Step 2: Identify the lepton number of X
If the lepton number must be conserved, X must also have a lepton number of –1
Step 3: State the particle X
Particle X is an anti-neutrino
Examiner Tips and Tricks
No need to fret about memorising all the different lepton numbers - the lepton number of each lepton and anti–lepton is provided on the datasheet. Remember that although quarks are fundamental particles, they have a lepton number of 0 and are classed as baryons.
Muon Decay
Muons are leptons that are slightly heavier than the electron
Muons (μ–) typically decay into an electron
Anti-muons (μ+) typically decay into positrons

The Feynman diagram for muon decay
Muon decay occurs through the weak interaction
This can be recognised by the exchange of the W– boson on a Feynman diagram
Worked Example
Show that muon decay satisfies all the conservation laws.
Answer:
Step 1: Write out the equation for muon decay
μ– → e– + ṽe + νμ
Step 2: List the quantities which must be conserved in this interaction
Charge, q
q = –1 for electrons and muons, q = 0 for neutrinos
Electron lepton number, Le
Le = +1 for electrons, Le = –1 for anti-electron neutrinos, Le = 0 for muons and muon neutrinos
Muon lepton number, Lμ
Lμ = +1 for muons and muon neutrinos, Lμ = 0 for electrons and electron neutrinos
Step 3: Determine if each quantity balances on each side of the equation
Charge, q:
μ– → e– + ṽe + νμ
–1 = –1 + 0 + 0 ✓ conserved
Electron lepton number, Le:
μ– → e– + ṽe + νμ
0 = +1 – 1 + 0 ✓ conserved
Muon lepton number, Lμ:
μ– → e– + ṽe + νμ
+1 = 0 + 0 + 1 ✓ conserved
Step 4: Write a conclusion
The numbers on each side of the equation are equal for charge, electron lepton number and muon lepton number, therefore, muon decay satisfies these conservation laws

Unlock more, it's free!
Did this page help you?