Particles, Antiparticles & Photons (AQA A Level Physics) : Revision Note
Antimatter
The Universe consists of matter in the form of particles i.e. protons, neutrons, electrons, etc.
All particles of matter have an antimatter counterpart
Antimatter particles are identical to their matter counterpart but have an opposite charge
This means if a particle is positive, its antimatter particle is negative, and vice versa
Common matter-antimatter pairs are shown in the table below:
Matter-Antimatter Table

Apart from electrons, the corresponding antiparticle has
The same name with the prefix ‘anti-’
A line above its corresponding matter particle symbol
Did this video help you?
Properties of Antiparticles
Corresponding matter and antimatter particles have
Opposite charges
The same mass
The same rest mass-energy
The rest mass-energy of a particle is the energy equivalent to the mass of the particle when it is at rest
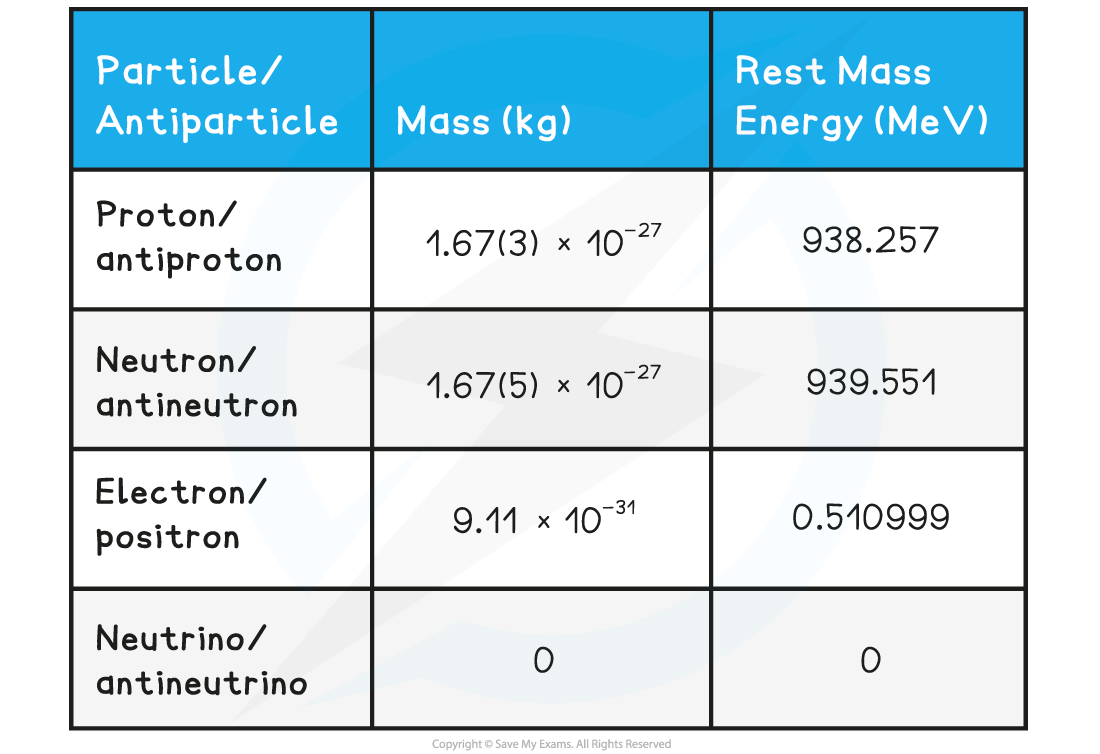
Some values of common particle masses and rest mass-energies are shown in the table below:
Mass & Rest Mass Energy Table
Examiner Tips and Tricks
In the exam, don't forget that the datasheet provides masses in kg and rest-mass energies in MeV for a proton, neutron, electron and neutrino
The Photon Model
Photons are fundamental particles which make up all forms of electromagnetic radiation
A photon is defined as:
A massless “packet” or a “quantum” of electromagnetic energy
This means that energy is not transferred continuously but as discrete packets of energy
In other words, each photon carries a specific amount of energy, or "quanta", and transfers it all in one go, rather than supplying it consistently
Calculating Photon Energy
The energy of a photon can be calculated using the formula:
Using the wave equation, photon energy can also be written:
Where:
E = energy of the photon (J)
h = Planck's constant (J s)
c = the speed of light (m s-1)
f = frequency (Hz)
λ = wavelength (m)
This equation tells us:
The higher the frequency of EM radiation, the higher the energy of the photon
The energy of a photon is inversely proportional to the wavelength
A long-wavelength photon of light has a lower energy than a shorter-wavelength photon

The energy of a photon is linked to the frequency of the light wave by the Planck constant, h
Worked Example
Light of wavelength 490 nm is incident normally on a surface, as shown in the diagram.
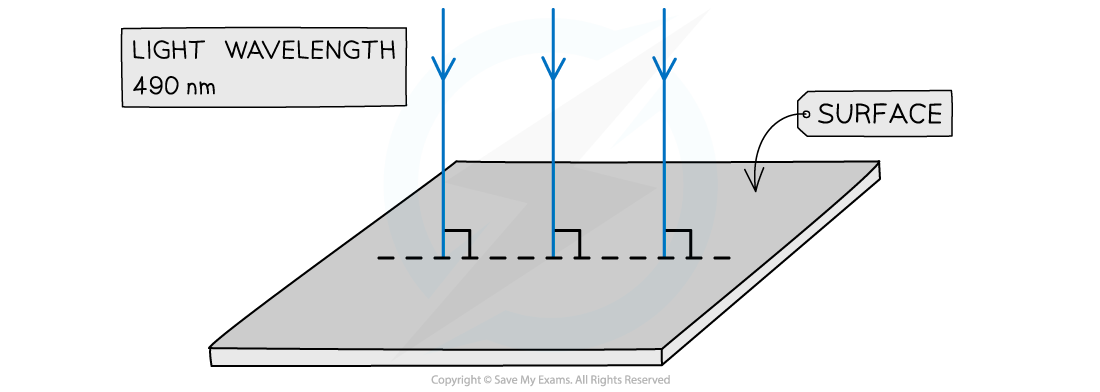
The power of the light is 3.6 mW. The light is completely absorbed by the surface.
Calculate the number of photons incident on the surface in 2.0 s.
Answer:
Step 1: Write down the known quantities
Wavelength,
Power,
Time,
Step 2: Write down the equations for wave speed and photon energy
Wave speed:
Photon energy:
Step 3: Calculate the energy of one photon
Step 4: Calculate the number of photons hitting the surface each second
Step 5: Calculate the number of photons that hit the surface in 2.0 s
Examiner Tips and Tricks
Make sure you learn the definition for a photon: discrete quantity / packet / quantum of electromagnetic energy are all acceptable definitions. The values of Planck’s constant and the speed of light will always be available on the datasheet, however, it helps to memorise them to speed up calculation questions!
Annihilation & Pair Production
Two important interactions involving particles, antiparticles and photons are:
Annihilation
Pair production
Annihilation
When a particle meets its corresponding antiparticle, the two will annihilate
Annihilation is defined as:
The destruction of a particle-antiparticle pair when they collide and convert their mass into two gamma-ray photons
The two most common particle-antiparticle pairs that are seen are:
Proton-antiproton annihilation
Electron-positron annihilation
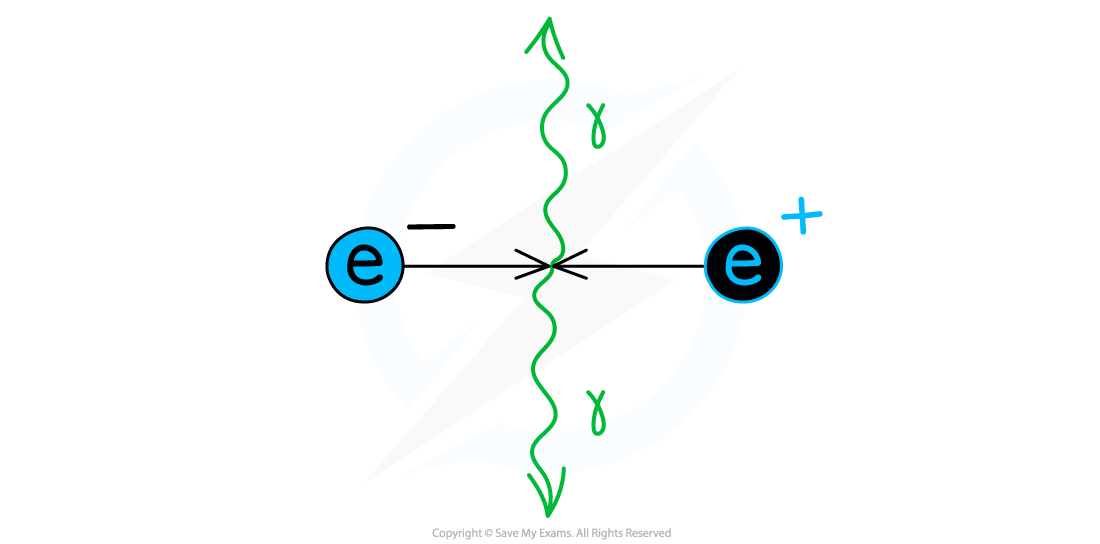
When an electron and positron collide, their mass is converted into energy in the form of two photons emitted in opposite directions
The minimum energy of one photon after annihilation is the total rest mass energy of one of the particles:
Where:
= minimum energy of one of the photons produced (J)
= Planck's Constant (J s)
= minimum frequency of one of the photons produced (Hz)
= rest mass energy of one of the particles (J)
To conserve momentum, the two photons will move apart in opposite directions
As with all collisions, the mass and energy is still conserved
Pair Production
Pair production is the opposite of annihilation, it is defined as:
The creation of a particle-antiparticle pair when a high-energy photon spontaneously converts its energy into mass
To achieve pair production, a single photon must have enough energy to create both particles
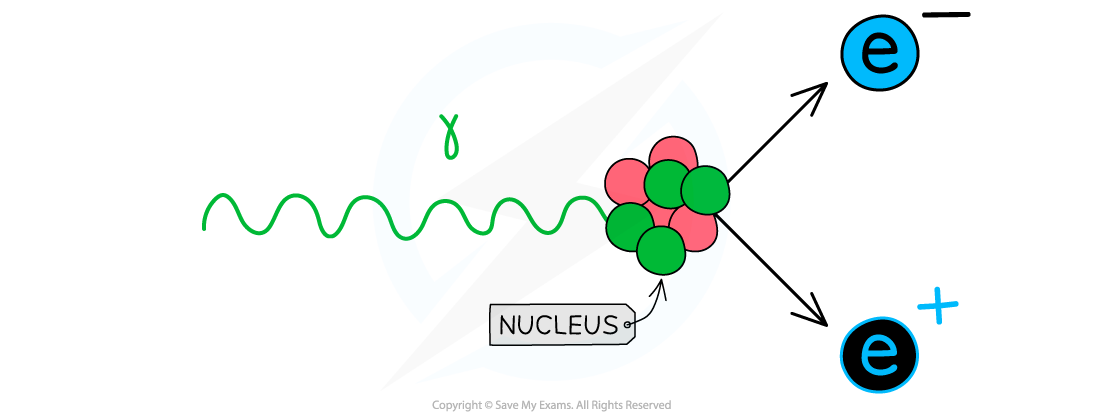
When a photon with enough energy interacts with a nucleus it can produce an electron-positron pair
The minimum energy required for a photon to undergo pair production is equal to the total rest mass energy of the particles produced:
Where:
= minimum energy of the incident photon (J)
= Planck's Constant (J s)
= minimum frequency of the photon (Hz)
= rest mass energy of one of the particles (J)
To conserve momentum, the particle and the antiparticle move apart in opposite directions
Worked Example
Calculate the maximum wavelength of one of the photons produced when a proton and antiproton annihilate each other.
Answer:
Step 1: Write down the known quantities
Rest mass of a proton (and antiproton) =
Step 2: Write down the equation for minimum photon energy
Step 3: Rearrange for the maximum photon wavelength
Step 4: Calculate the maximum photon wavelength
Examiner Tips and Tricks
Since the Planck constant is in Joules (J) remember to always convert the rest mass-energy from MeV to J.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
