Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesTurning Points in PhysicsSpecial RelativityRelativistic Energy

Relativistic Energy (AQA A Level Physics)

Revision Note

Dan Mitchell-Garnett

Last updated

Relativistic Energy

Relativistic Kinetic Energy

  • We know that an object in motion relative to an observer has energy E = (γm0)c2 and its rest energy is E0 = m0c2

    • The kinetic store is the energy store associated with motion

    • If an object in motion has a total energy E which is greater than its rest mass E0, the additional energy must be in the kinetic store

E subscript k space equals space m c squared space minus space m subscript 0 c squared

  • Where:

    • Ek is energy in the kinetic store

    • m is relativistic mass

    • m0 is the object's rest mass

    • c is the speed of light

  • This can be rearranged for an expression for the total energy, E, of a particle:

E space equals space m c squared

E space equals space m subscript 0 c squared space plus space E subscript k

  • The total energy of an object increases at a rapidly increasing rate as it's speed approaches the speed of light

Graph showing how total energy increases as an object's speed approaches the speed of light

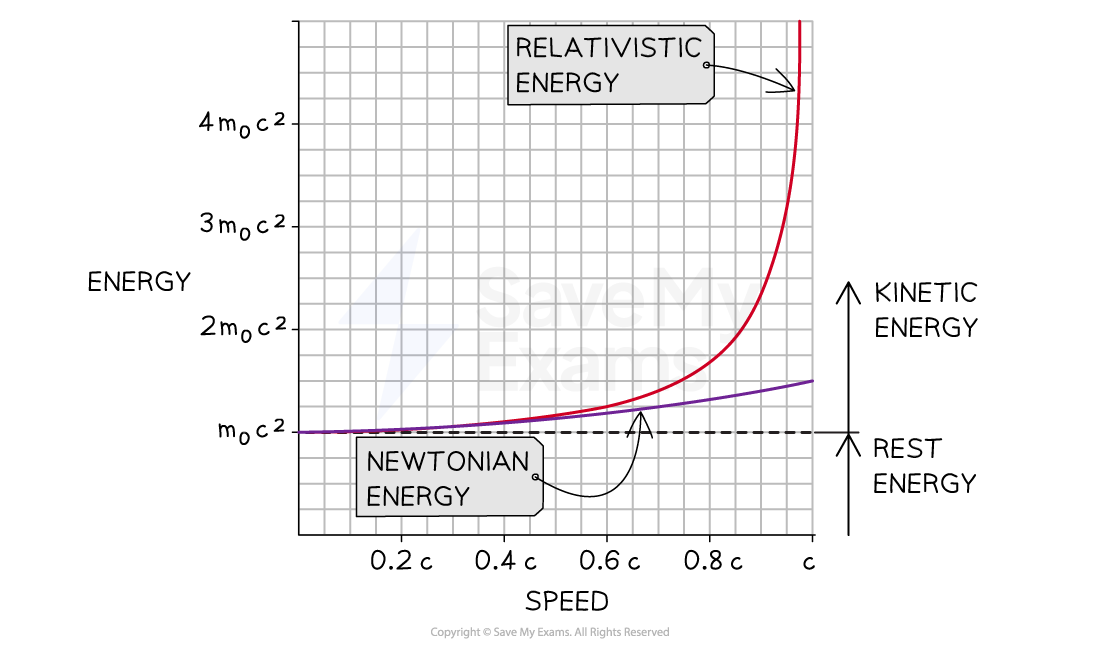
12-3-9-energy-vs-speed

  • As with mass on the previous page, the asymptote on this graph shows that an infinite amount of energy is needed to make an object with mass reach the speed of light

Worked Example

A spacecraft with a proper mass of 450 kg accelerates to a speed of 0.7c. Calculate the difference in its relativistic kinetic energy and its kinetic energy calculated using Newtonian physics.

Answer:

Step 1: List the known quantities:

  • Rest mass, m0 = 450 kg

  • Speed, v = 0.7c

  • Speed of light, c = 3.0 × 108 ms-1

Step 2: List the relevant equations:

  • Newtonian kinetic energy, Ekn = ½m0v2

  • Relativistic kinetic energy, Ekr = γm0c2 − m0c2

Step 3: Calculate the Newtonian kinetic energy:

  • Substitute the known quantities:

E subscript k n end subscript space equals space 1 half space cross times space 450 space cross times space open parentheses 0.7 space cross times space open parentheses 3.0 space cross times 10 to the power of 8 close parentheses close parentheses squared space equals space 9.9 space cross times space 10 to the power of 18 space straight J

Step 4: Calculate the gamma term:

  • Substitute the speed into the gamma term:

gamma space equals space fraction numerator 1 over denominator square root of 1 space minus space v squared over c squared end root end fraction

gamma space equals space fraction numerator 1 over denominator square root of 1 space minus space open parentheses 0.7 c close parentheses squared over c squared end root end fraction space equals space fraction numerator 1 over denominator square root of 1 space minus space 0.7 squared end root end fraction space equals space 1.40

Step 5: Substitute the gamma term into the relativistic kinetic energy equation:

  • Substitute the rest mass, speed of light and speed as well:

E subscript k r end subscript space equals space gamma m subscript 0 c squared space minus space m subscript 0 c squared space equals space m subscript 0 c squared open parentheses gamma space minus space 1 close parentheses

E subscript k r end subscript space equals space 450 space cross times space open parentheses 3.0 space cross times space 10 to the power of 8 close parentheses squared space cross times space open parentheses 1.40 space minus space 1 close parentheses space equals space 1.6 space cross times space 10 to the power of 19 space straight J

Step 6: Calculate the difference between the two kinetic energies:

  • Subtract the smaller Newtonian kinetic energy from the larger relativistic energy

straight capital delta E subscript k space equals space open parentheses 1.6 space cross times space 10 to the power of 19 close parentheses space minus space open parentheses 9.9 space cross times space 10 to the power of 18 close parentheses space equals space 6.1 space cross times space 10 to the power of 18 space straight J

  • As you can see, the relativistic kinetic energy is almost twice as large as the Newtonian kinetic energy!

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Relativistic MassNext:Bertozzi's Experiment
    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.