Relativistic Mass

Equivalence of Mass & Energy

Einstein showed in a1905 paper that matter can be considered a form of energy and hence, he proposed:
- Mass can be converted into energy
- Energy can be converted into mass
This is known as mass-energy equivalence, and can be summarised by the equation:

$E = m c^{2}$

Where:
- E = energy (J)
- m = mass (kg)
- c = the speed of light (m s^-1)
Scenarios where mass is converted to energy or energy to mass include:
- The fusion of hydrogen into helium in the centre of the Sun
- The fission of uranium in nuclear power plants
- Nuclear weapons
- High-energy particle collisions in particle accelerators

An object's proper mass (that is, its mass measured by an observer at rest relative to the object) is also called its rest mass, m₀
An observer in an inertial reference frame moving at speed v relative to the object measures the object's mass as m, which is given by:

$m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

This can also be written as:

$m = γ m_{0}$

Because γ > 1, when an object is moving relative to your frame of reference, you measure its mass as larger than it's rest mass
- The derivation for this relativistic mass is a good deal more complex than the derivation for relativistic time and length and is not examinable so it is omitted from this revision note
One interesting outcome of this relativistic mass is the speed limit imposed on objects
- As an object's speed nears the speed of light, it's mass gets larger and larger
- Very close to the speed of light, an object's mass tends towards an infinite mass

Graph showing how relativistic mass changes with velocity

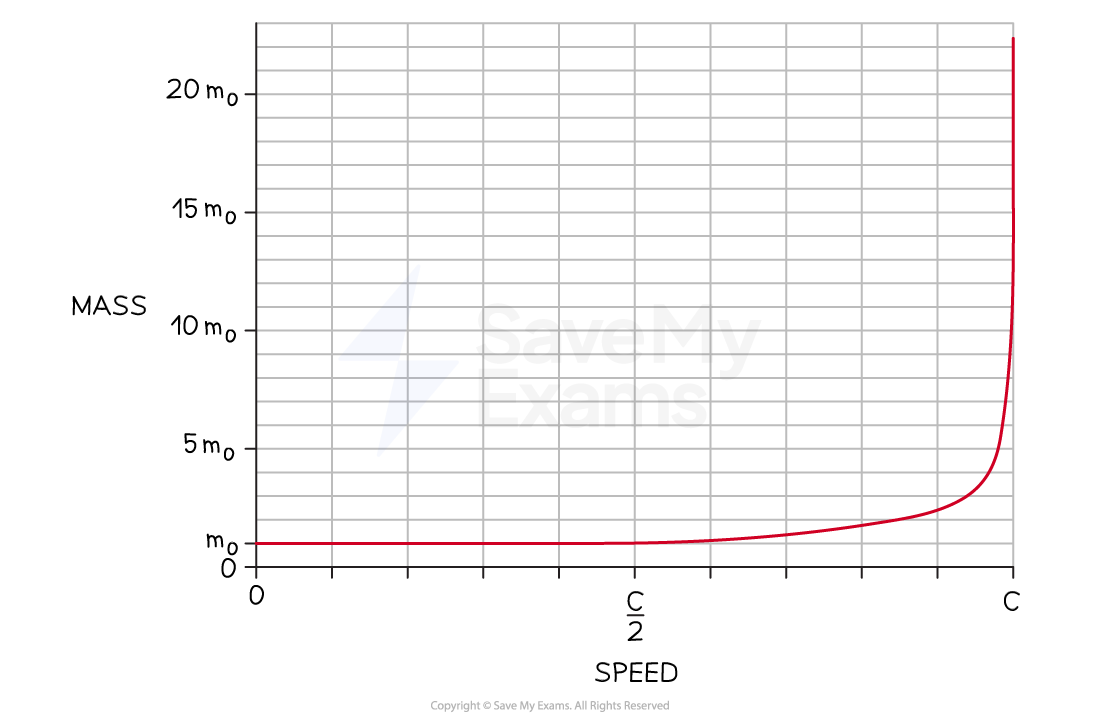
12-3-8-mass-vs-speed

The effect of speed, as a fraction of c, on an object's mass, in multiples of rest mass. Mass increases rapidly as the object's speed approaches c.

Relativistic Energy

Let's reconsider Einstein's famous equation, taking relativistic effects into account:

$E = (γ m_{0}) c^{2}$

$E = \frac{m_{0} c^{2}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

The mass of a stationary object is its rest mass, m₀, so it has a rest energy of E = m₀c²

Worked example

A particle in a particle accelerator has a rest mass of M₀ and is accelerated to a maximum speed of 0.998c.

Calculate the total energy of the particle at its maximum speed, as a multiple of its proper energy, from the reference frame of an observer who is stationary relative to the accelerator.

Answer:

Step 1: List the known quantities:

Maximum speed, v = 0.998c

Step 2: Write down the relevant equations:

Rest energy, E₀ = m₀c²
Relativistic energy, E = γm₀c²
Write the equation with the gamma term out in full

$E = \frac{m_{0} c^{2}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

Step 3: Substitute the known quantities:

The relativistic energy in terms of rest mass M₀ is

$E = \frac{M_{0} c^{2}}{\sqrt{1 - \frac{{(0.998 c)}^{2}}{c^{2}}}} = \frac{M_{0} c^{2}}{\sqrt{1 - 0 . 998^{2}}} = 15.8 M_{0} c^{2}$

Step 4: Give the answer as a multiple of proper energy:

Proper energy is another way of saying rest energy, which is M₀c²
The particle's energy is 15.8 times larger than the rest energy, according to the observer

Examiner Tip

When you see a speed and a mass, it's tempting to go into auto-pilot and stick everything into the equation E_k = ½mv², but this would gain you no marks in this worked example! The trick is to look at how large the speed is, if it is close to the speed of light, the relativistic effects are significant and you need to account for them. The context of the question can also provide clues, such as mentioning frames of reference or rest mass.

Relativistic Mass (AQA A Level Physics)

Revision Note

Equivalence of Mass & Energy