Time Dilation (AQA A Level Physics): Revision Note

Time Dilation

• When objects travel close to the speed of light, to an observer moving relative to that object, it looks as if the object has slowed down 

  • This is best demonstrated by clocks

• Observer H is in a rocket moving close to the speed of light

  • They will see their clock ticking at a regular pace, say, it is reading 15:00

• Observer G at rest on Earth, with remarkable eyesight, will measure the clock as ticking slower

  • They will observe that time has slowed down in the spaceship from their reference frame i.e. they may see the time as 14:45 instead of 15:00

• However, the same occurs the other way around

• For observer H on the rocket, it is observer G that is moving relative to them 

  • Therefore, observer H will measure observer G's clock as ticking slower i.e. they see time slow down on Earth from their reference frame

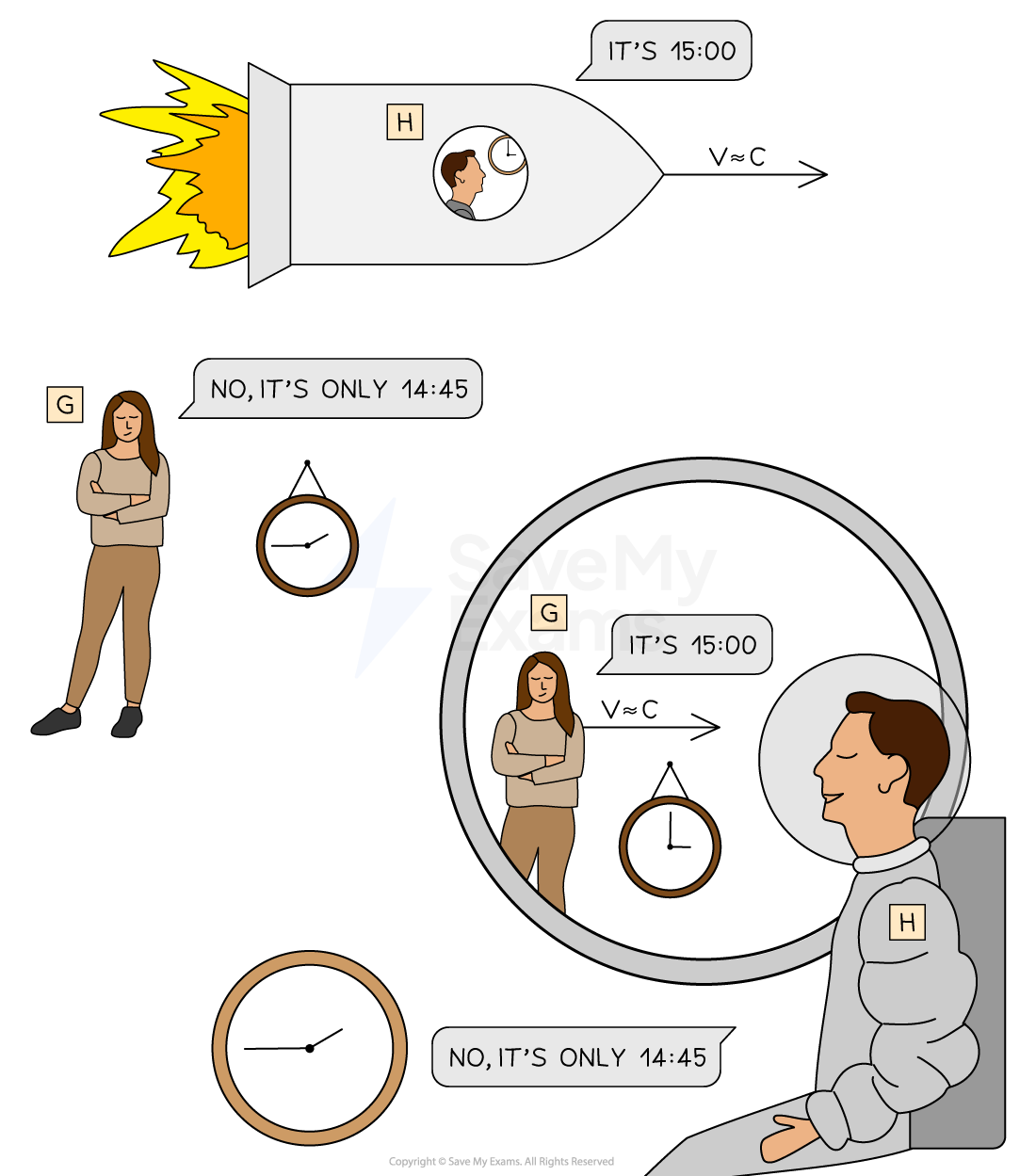
A stationary observer in their reference frame views clocks as running slower in the moving reference frame. We're back to disagreeing

The Gamma Term

• Recall from Einstein's Postulates that moving between frames of reference means the speed needs to be changed through simple addition or subtraction

  • When travelling at speeds close to the speed of light, this no longer applies, because the speed of light is independent of the frame of reference

• This transformation from one reference frame to another is corrected by multiplying by a scaling factor called the gamma factor, $\gamma$

$\gamma =\frac{1}{\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}}$

• As v  is always less than c  (the speed of light), this means $\gamma$  is always greater than 1

• This is especially important for time dilation and length contraction

  • We will use time dilation to explain where this gamma term comes from

Time Dilation Equation

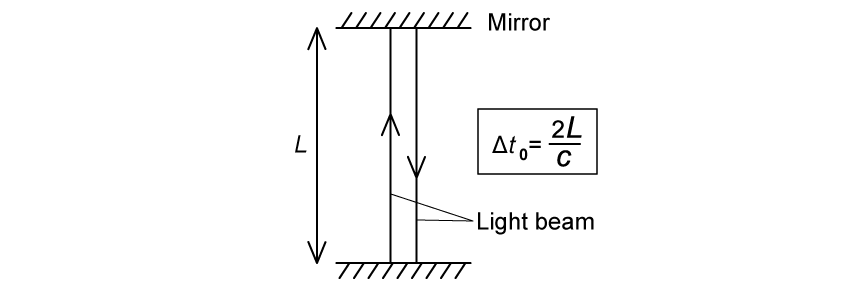
• Consider a light clock. This consists of two mirrors facing each other with a beam of light travelling up and down between them 

• An observer is at rest relative to the clock on a train platform and watches the light reflect between the mirrors

• The distance between the mirrors is L and the light travels at a speed c

• Therefore, the time interval for the light to travel from the top mirror back down to the bottom is: 

$\mathrm{\Delta }{t}_0=\frac{2L}{c}$

• Another light clock is on a moving train, relative to the initial observer on the platform, travelling at constant velocity v

  • This velocity v  is close to the speed of light 

• The stationary observer on the platform sees the light clock on the train and watches the reflection of the rays between the mirrors

• It appears that the light rays travel to the right at an angle to the direction of motion

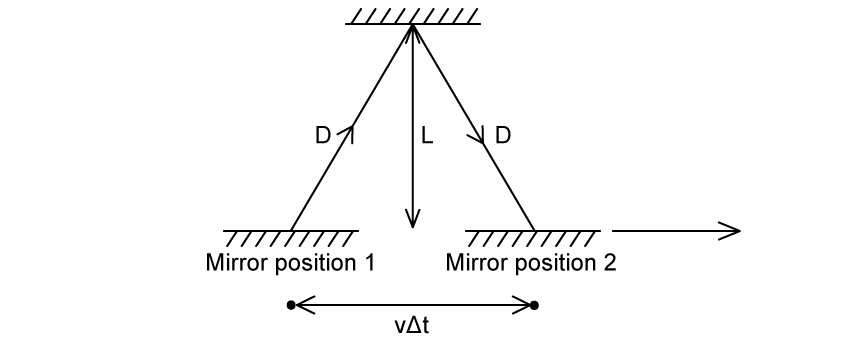
• The observer on the train platform sees the mirror at:

  • Position 1, when the light leaves the bottom mirror

  • Position 2, when the light returns to it

• The distance between the mirrors, L, is the same, but the light now travels a longer path, D

• The distance travelled by the light ray is now 2D, and the time observed between the reflections is now

$∆t=\frac{2D}{c}$

• The apparent distance horizontally travelled by the mirror is $v\mathrm{\Delta }t$ where v  is the speed of the train

• Notice that this is part of a right-angled triangle, so using Pythagoras' theorem we can see that:

$D^2=L^2+{\left(\frac{v^{}∆t}{2}\right)}^2$ 

• Where: 

$D=\frac{c∆t}{2}$

• We want to find $∆t$, the time taken for the light ray to travel up and down in the reference frame of the stationary observer on the train platform, who is moving relative to the light clock on the train

  • Remember, although it is the train that is moving, in the reference frame of an observer on the train it is the observer on the platform that is moving

$∆t=\frac{{\displaystyle \frac{2L}{c}}}{\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}}=\frac{∆t_0}{\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}}$

• Remember the gamma factor $\gamma =\frac{1}{\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}}$

• Therefore:

$∆t=\gamma ∆t_0$

• Where:

  • $∆t$ = the time interval measured from an observer moving relative to the time interval being measured (s)

  • $∆t_0$ = the proper time interval (s)

• As $\gamma$ > 1, this means that the $∆t>∆t_0$

  • In other words, a clock observed from a reference frame moving relative to it will be measured to tick slower than a clock that is at rest in its frame of reference

• The observer on the platform will view the train clock as moving slower

• The observer on the train will view the platform as moving slower

• You may be wondering why it's the time that slows down for the light beam, and not the light beam just speeding up to hit each mirror at the same frequency

  • This is due to Einstein's second postulate

  • Both Observers G and H must measure the speed of light to be c, so it doesn't slow down or speed up according to either reference frame

• It is important to note that the time has been measured at the same position

  • In other words, the time interval is the position at which the light leaves the first mirror and at which it returns to the second mirror in the reference frame of the mirror