Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesTurning Points in PhysicsSpecial RelativityBertozzi's Experiment

Bertozzi's Experiment (AQA A Level Physics)

Revision Note

Dan Mitchell-Garnett

Last updated

Bertozzi's Experiment

How do you Measure Kinetic Energy?

  • When accelerating a particle with charge q  from rest, the work done by an electric field with potential difference V  is equal to the energy gained by the particle's kinetic store, Ek :

q V space equals space E subscript k

  • This gives a way of measuring the kinetic energy of a particle of known charge, such as an electron

What was Bertozzi's Experiment?

  • Bertozzi accelerated electrons to speeds close to the speed of light and measured their kinetic energies

    • The aim of the experiment was to plot the squared speeds of electrons against their kinetic energies and compare the results to Newtonian and relativistic predictions

  • A strong electric field was used to transfer energy to the kinetic store of the electrons

    • This meant that, for an electric field of potential difference V, each electron had a kinetic energy of eV, where e  is the magnitude of charge on an electron

    • These electrons were fired at an aluminium target

  • The speed of the electrons was simply calculated using distance divided by time

    • Once the electrons left the electric field, they travelled at constant speed, as no forces acted

    • A signal after the electric field and a signal attached to the aluminium target were used to measure a time interval using an oscilloscope

    • The distance was measured between the two signals and speed was calculated

A diagram outlining the experimental setup of Bertozzi's electron experiment

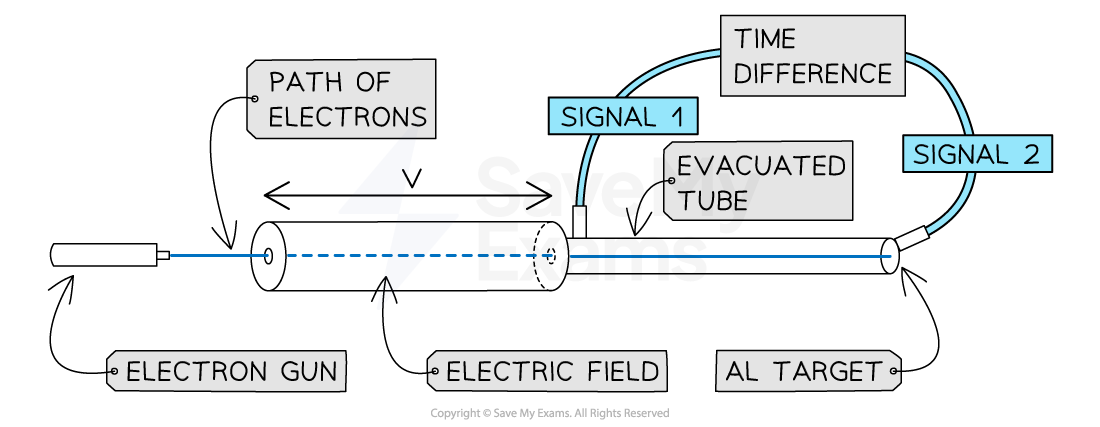
12-3-10-experimental-setup

Electrons are accelerated by an electric field and trigger a signal once they have left the field and trigger another when they hit the aluminium target, allowing speed to be calculated

The Results

  • With several values of speed-squared and kinetic energy, Bertozzi produced a graph showing the following results

A graph showing speed-squared against kinetic energies

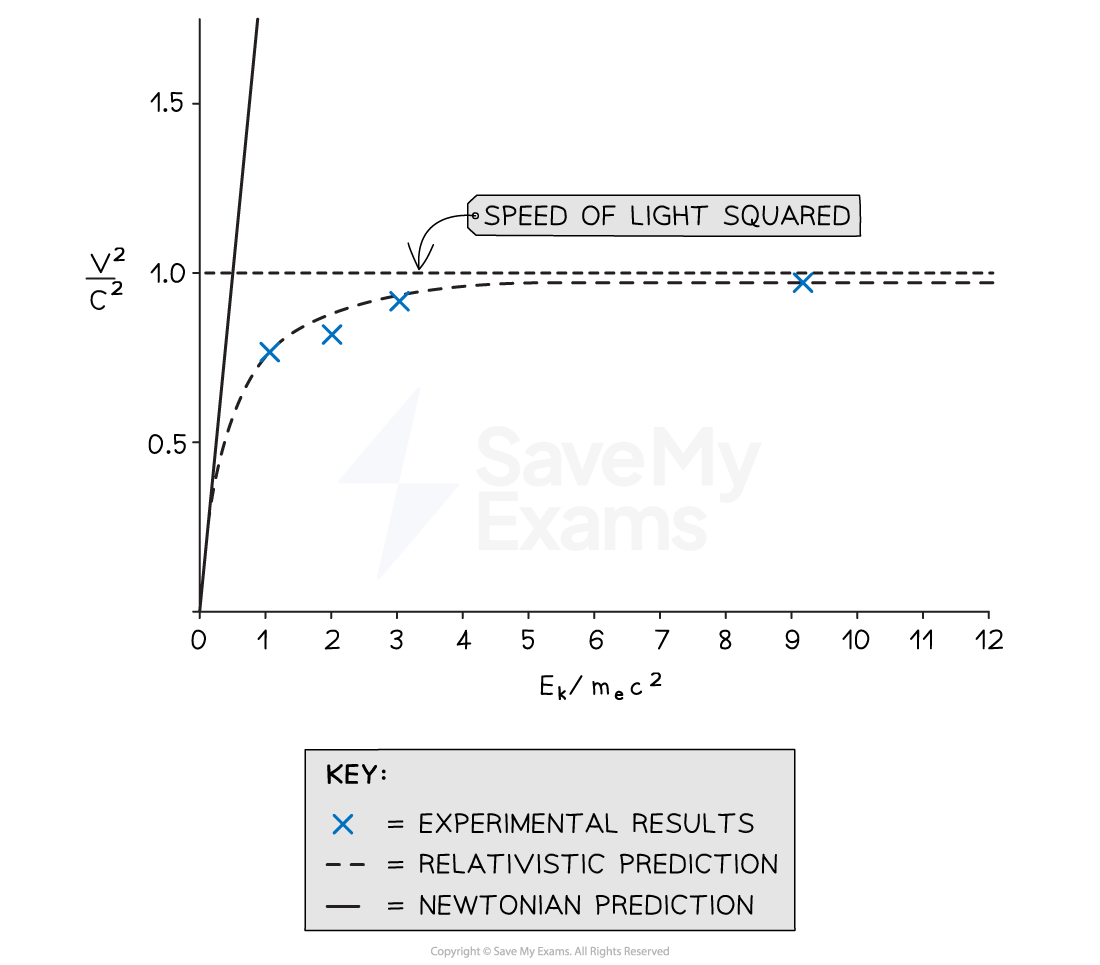
12-3-10-graph-results

This graph shows the kinetic energy of the electrons, with units of mec2, plotted against their squared speeds, with units of c2. The Bertozzi results agree closely with the relativistic predictions of speeds and show electrons cannot exceed the speed of light.

  • This experiment's data agreed with the relativistic predictions far more than the Newtonian predictions

Verifying the Kinetic Energy of the Electrons

  • To avoid any doubts about whether the electrons actually did have a kinetic energy equal to eV, Bertozzi and his team measured the kinetic energy of the electrons directly as they hit the aluminium target

  • They did this by measuring the temperature change of the target and using the equation ΔE = mcΔθ

    • This energy change is equal to the total kinetic energy lost by the incoming electrons

    • The total charge transferred to the target was used to calculate the number of electrons which hit the target

  • With total energy transferred to the target and the number of electrons known, the team could calculate the kinetic energy per electron

    • These values were in agreement with the energy transferred to the electrons by the electric field, showing the results were valid and the electrons behaved relativistically at speeds close to c

Worked Example

In a repeat of the Bertozzi experiment, electrons are fired through an evacuated tube at a 0.0250 kg aluminium plate. After the experiment has run for a time, the target has accumulated −6.20 μC of charge and has increased in temperature by 1.80 °C.

Calculate the kinetic energy per electron in units of MeV.

Specific heat capacity of aluminium = 902 J kg-1 K-1

Answer:

Step 1: List the known quantities

  • Mass of aluminium, m = 0.0250 kg

  • Specific heat capacity of aluminium, c = 902 J kg-1 K-1

  • Change in temperature, Δθ = 1.80 °C

  • Charge transferred to aluminium plate, Q = −6.20 μC

  • Charge of an electron, e = −1.60 × 10−19 C

Step 2: Write out the relevant equation

  • Thermal energy transferred to aluminium, ΔE = mcΔθ

Step 3: Calculate the energy transferred to the aluminium's thermal store

  • The thermal energy gained by the plate is:

straight capital delta E space equals space m c straight capital delta theta space equals space 0.0250 space cross times space 902 space cross times space 1.80 space equals space 40.59 space straight J

Step 4: Calculate the number of electrons incident on the aluminium plate

  • Each electron transfers a charge of e  to the plate

  • The total charge transferred to the plate divided by e  will give the number of electrons, n, incident on the plate:

n space equals space Q over e space equals space fraction numerator negative 6.20 space cross times space 10 to the power of negative 6 end exponent over denominator negative 1.60 space cross times space 10 to the power of negative 19 end exponent end fraction space equals space 3.875 space cross times space 10 to the power of 13

Step 5: Calculate the kinetic energy per electron

  • The total thermal energy gained by the plate is equal to the total kinetic energy, Ek,tot , of all the electrons hitting it

  • Ek,tot divided by the number of electrons gives the kinetic energy per electron, Ek :

E subscript k space equals space E subscript k comma t o t end subscript over n space equals space fraction numerator straight capital delta E over denominator n end fraction space equals space fraction numerator 40.59 over denominator 3.875 space cross times space 10 to the power of 13 end fraction space equals space 1.0475 space cross times space 10 to the power of negative 12 end exponent space straight J

Step 6: Convert the kinetic energy per electron into mega-electronvolts

  • Recall that 1 eV is equal to 1.60 × 10-19 J:

E subscript k space equals space fraction numerator 1.0475 space cross times space 10 to the power of negative 12 end exponent over denominator 1.60 space cross times space 10 to the power of negative 19 end exponent end fraction space equals space 6.547 space cross times space 10 to the power of 6 space eV

  • Finally, the answer must be to 3 significant figures, as all the figures in the question were given to this number:

E subscript k space equals space 6.55 space MeV

Examiner Tips and Tricks

You may be asked on either method of determining the kinetic energy of each electron so expect to see the thermal energy equation and work done by an electric field in this topic.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Relativistic Energy
    Dan Mitchell-Garnett

    Author: Dan Mitchell-Garnett

    Expertise: Physics Content Creator

    Dan graduated with a First-class Masters degree in Physics at Durham University, specialising in cell membrane biophysics. After being awarded an Institute of Physics Teacher Training Scholarship, Dan taught physics in secondary schools in the North of England before moving to Save My Exams. Here, he carries on his passion for writing challenging physics questions and helping young people learn to love physics.