Electron Diffraction (AQA A Level Physics): Revision Note
Exam code: 7408
Electron Diffraction
Do Electrons Diffract?
To investigate whether electrons did exhibit wave-like properties, an electron diffraction tube was produced
The electrons were accelerated in an electron gun with a high potential difference, such as 5000 V, and were then directed through a thin film of graphite
The gaps between the carbon atoms were sufficiently small to cause diffraction, using the predicted DeBroglie wavelength of electrons
Diffraction is a property of waves when passing through a small gap - if the electrons were seen to diffract then this was proof of their wave-like properties
The electrons were indeed seen to diffract from the gaps between carbon atoms and produce a circular pattern on a fluorescent screen made from phosphor
Diagram of the electron diffraction experiment
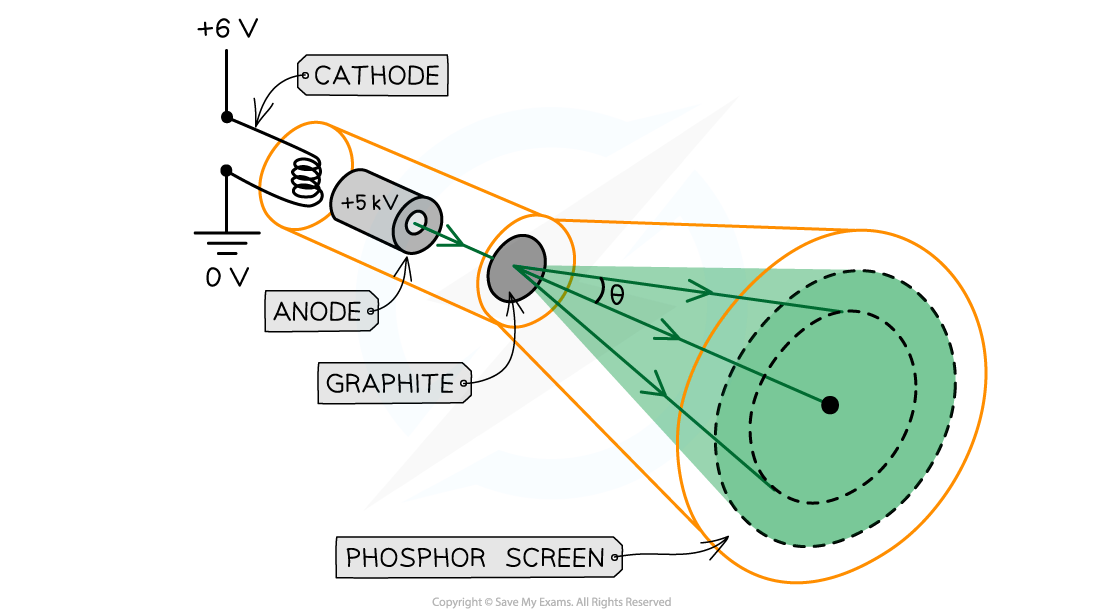
A low voltage causes thermionic emission of electrons at the cathode, then these are accelerated towards anode directed through the graphite. The electrons diffract through the gaps between atoms in the graphite, forming a circular diffraction pattern made visible by the phosphor screen.
The Effect of Potential Difference on the Diffraction Pattern
Recall that DeBroglie's hypothesis predicted that, if more work was done on the electrons, their wavelength would be shorter
Recall from the diffraction grating subtopic of the Waves topic, that a shorter wavelength leads to a smaller diffraction angle θ for a given gap width
Therefore, if DeBroglie was right, increasing the potential difference would cause the diffraction rings to move closer to the centre of the phosphor screen
Diagram showing the effect of increasing potential difference on diffraction
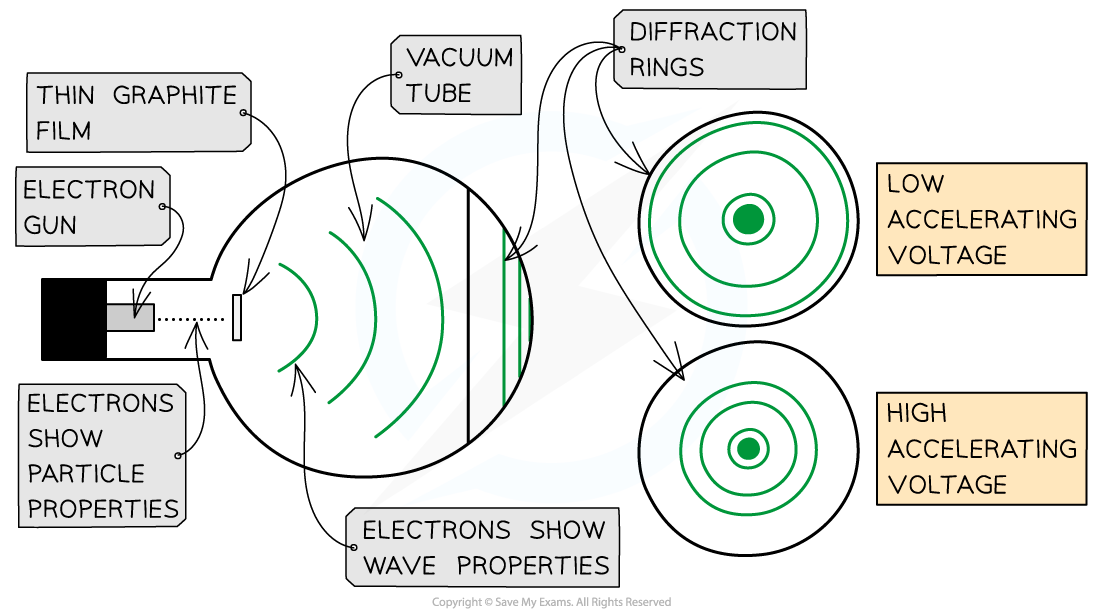
The left of this diagram shows the equipment from another angle. The right of this diagram shows that increasing the voltage caused the diffraction rings to move closer to the centre of the screen, following DeBroglie's equation.
This was the first experimental proof of electrons exhibiting wave-like properties
The wavelength of electrons was significantly smaller than high energy forms of electromagnetic radiation, such as X-rays
Examiner Tips and Tricks
This topic builds on knowledge acquired from studying diffraction gratings. As is becoming a common theme with Turning Points, go back and make sure your understanding of diffraction is solid before getting stuck in with this topic.
Estimate of Anode Voltage
Changing the voltage across the anode (it is the voltage that causes the electrons to accelerate), scientists can manipulate the wavelength of the electron
A microscope's resolving power (its ability to differentiate between two nearby points on an object) depends on the wavelength of the radiation being used
A shorter wavelength means the microscope can be used to see finer details in an object
Electrons had wavelengths much shorter than X-rays
The size of an atom is roughly 10−10 m
By using DeBroglie's equation for an accelerated electron, researchers could find the accelerating voltage needed to make the electron's wavelength the same size as an atom
Worked Example
An atom of carbon has a diameter of 1.5 × 10−10 m. Determine the anode potential difference needed in an electron diffraction tube to produce electrons with a wavelength equal to the diameter of a carbon atom.
Answer:
Step 1: Write down the equation for wavelength of accelerated electrons from the data and formulae booklet:
The wavelength of an accelerated electron is:
Step 2: List the known quantities:
Mass of an electron, m = 9.11 × 10−31 kg
Magnitude of charge on an electron, e = 1.60 × 10−19 C
Planck's constant, h = 6.63 × 10−34 J s
Required wavelength of the electron, λ = 1.5 × 10−10 m
Step 3: Rearrange the wavelength equation to make anode potential difference the subject:
Separate the V term from the square root:
Square the whole equation:
Step 4: Substitute the known quantities:
Examiner Tips and Tricks
In a high pressure situation like an exam, it's easy to make mistakes on your calculator when substituting values in standard form. Use brackets carefully and retype your equation to ensure you get the same value when checking over your answers.
Unlock more, it's free!
Join the 100,000+ Students that ❤️ Save My Exams
the (exam) results speak for themselves:
Was this revision note helpful?
Build on this topic
