Fizeau's Speed of Light Experiment (AQA A Level Physics)

Fizeau's Determination of the Speed of Light

• Scientists used to believe that light covered distance instantaneously and travelled at infinite speed

  • Some astronomical observations seemed to contradict this, however

  • Following this, Hippolyte Fizeau measured a finite speed for light

How did Fizeau measure the speed of light?

• Fizeau shone a beam of light at a mirror several kilometres away

• In the path of the light, he placed a "toothed wheel" which was spinning at a very high speed

  • The toothed wheel was positioned so the teeth of the wheel and the gaps between them periodically passed over the beam of light

  • This created regular pulses of light travelling towards the distant mirror

The path of the light passing through a gap in the toothed wheel

Light from the source was continuous, but the toothed wheel caused the mirror to receive periodic bursts of light. The light here passes through a particular gap, labelled G, while the toothed wheel rotates.

• In the example shown in the diagram, the light passes through a particular gap, labelled G

• The light had to travel a distance d  from the source to the mirror and then back to the observer

  • The total path length of the light was 2d  and the speed of light was labelled c

  • The total time for the light to pass through the toothed wheel and return was:

• The speed at which the wheel rotated could be changed - at a certain wheel speed, the light on its returning path would hit the tooth next to G

  • This meant the observer would see no light returning from the mirror 

Diagram showing the returning light blocked by a tooth

In the previous diagram, the initial beam of light passed through gap G. The wheel then kept rotating. By the time the light has travelled to the mirror and returned, gap G has now been replaced with the tooth next to it and the light is blocked.

• The wheel's rotational speed is increased slightly

  • Now, by the time the light that passed through G has returned, G has been replaced with the next gap

  • The returning light passes through this gap and the observer sees reflected light through the toothed wheel

Diagram showing the returning light passing through the next gap

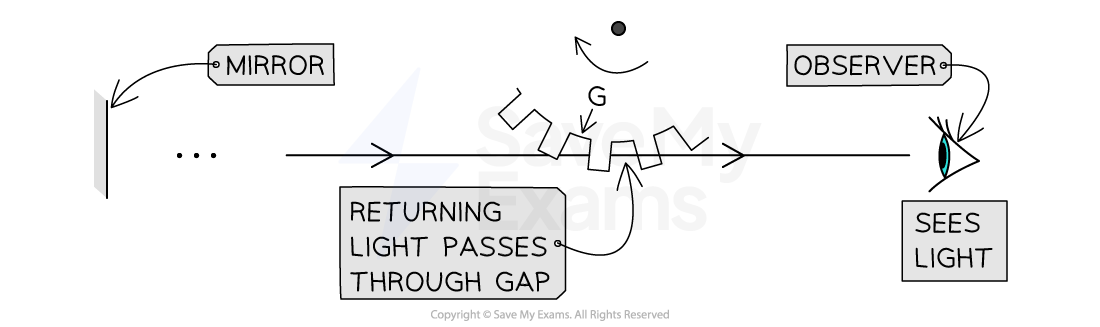
At this rotational speed, the same thing happens for light passing through every gap. The time of the light's path is equal to the time taken for one gap to be replaced by the next gap.

• The toothed wheel has n  gaps and n  teeth which both have the same width

  • This means that, if a full revolution has a period of T, then the time taken for a gap to be replaced by a tooth is:

• Recall that time period is the reciprocal of frequency f  (of teeth passing a point per second) so we can write this as:

• When the observer sees the reflected light disappear, the time taken for light to travel to the mirror is the time taken for a gap to be replaced by a tooth, so:

• Rearranging this allowed Fizeau to calculate the speed of light as:

Other Experiments done by Fizeau

• Fizeau also measured the speed of light in water by a similar method and found it to be slower than the speed of light in air

  • This was another piece of evidence contradicting Newton's corpuscular theory - recall that this predicted light would travel faster in a denser medium