Stokes' Law

Motion of a Falling Oil Droplet

Motion of the Oil Droplet without the Electric Field

Millikan's experiment was designed to determine the charge of oil droplets, and therefore the charge on electrons
- To calculate charge using the condition for stationary oil droplets, however, the mass of each oil droplet was required
With the electric field turned off, the oil droplets fell at terminal velocity
- This means their weight, mg, was balanced by drag forces as they passed through the air
- Millikan timed the oil drops as they passed the window of his apparatus to determine their speeds

A diagram showing weight and drag forces on an oil droplet

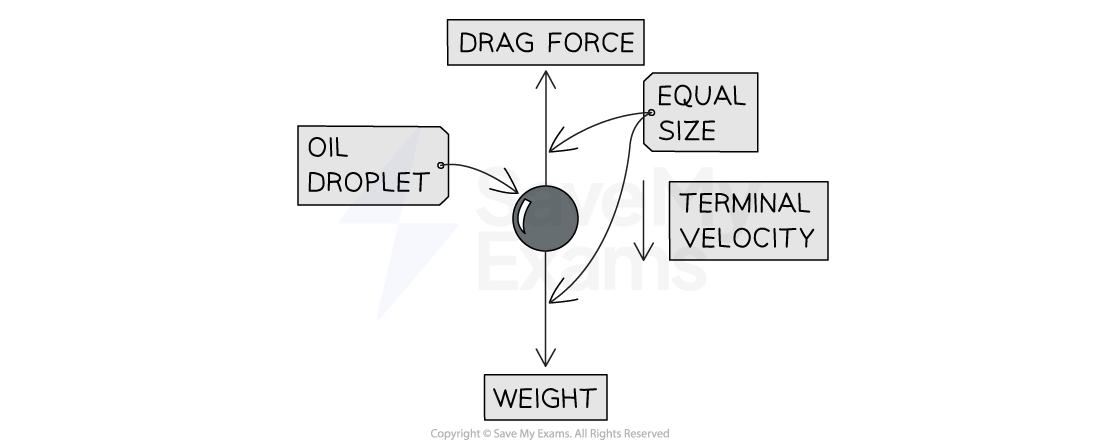
12-1-6-drag-forces-on-a-oil-droplet

At terminal velocity, speed is constant and resultant force is zero, so weight is balanced by drag forces

Viscous Drag Force using Stokes' Law

In fluid dynamics, Stokes' law allows drag force on an object through a fluid (such as air) to be calculated, provided:
- The object is small
- The object is spherical
- The speed is low
Stokes' law states that, for an object with radius r moving at velocity v through a fluid with viscosity η, the viscous drag force, F, is:

$F = 6 π η r v$

Calculating Mass from Stokes' Law

Recall that the drag force and weight are equal at terminal velocity, so:

$6 π η r v = m g$

Both mass and radius are unknown, but we can write mass in terms of radius for a sphere of known density, ρ :

$m = ρ V = \frac{ρ 4 π r^{3}}{3}$

Combining these equations allowed Millikan to determine the radius, and therefore mass, of an oil drop whose velocity was known
- Recall the condition for a stationary oil drop:

$\frac{Q V}{d} = m g$

- This now gave Millikan enough information to calculate the charge Q on an oil drop if he knew its terminal velocity and the potential difference V required to make it stationary

Significance of Millikan's Results

Millikan repeated his experiment for many different oil droplets
- They all had different charges, but he noticed an interesting pattern in his results
- Every value of charge was an integer multiple of 1.60 × 10⁻¹⁹ C

Table of results from Millikan's Experiment

Oil Droplet Number	Charge on Droplet (× 10⁻¹⁹ C)	Charge divided by 1.60 × 10⁻¹⁹ C
1	1.59	0.994
2	11.1	6.94
3	9.54	5.96
4	15.9	9.94
5	6.36	3.98

Millikan's results showed that the charge on each oil drop was an integer multiple of 1.60 × 10⁻¹⁹ C

Quantisation of Electric Charge

Each negative oil droplet had been ionised, so carried an integer number of electrons
- The fact that each droplet's charge was quantised into integer multiples of 1.60 × 10⁻¹⁹ C suggested that this was the charge of each electron

Worked example

Using Stokes' Law, show that the droplet's mass m can be expressed in terms of its velocity v, the viscosity of air η, the density of the oil ρ and acceleration due to gravity g, as:

$\frac{6 π η v}{g} \sqrt{\frac{9 η v}{2 ρ g}}$

Answer:

Step 1: Write down the relevant equation from the data and formulae sheet

Stokes' law:

$F = 6 π η r v$

Step 2: Apply Stokes' law to the droplet at terminal velocity

At terminal velocity (in the absence of an electric field), weight is equal to viscous drag force:

$m g = 6 π η r v$

Step 3: Write mass in terms of radius and density

We need to get rid of the radius term as it will not be in our final expression
- We can do this by writing radius in terms of the required quantities
Recall the equation relating mass, density and volume of a sphere, V_s:

$m = V_{s} ρ$

$m = \frac{4 π r^{3} ρ}{3}$

Step 4: Write an expression for the droplet's radius

Substitute the expression for mass in terms of radius and density and rearrange for radius:

$\frac{4 π r^{3 2} ρ g}{3} = 6 π η r v$

$r^{2} = \frac{9 η v}{2 ρ g}$

$r = \sqrt{\frac{9 η v}{2 ρ g}}$

Step 5: Substitute this into the expression for mass

We can finally eliminate radius from the equation in step 2:

$m = \frac{6 π η r v}{g}$

$m = \frac{6 π η v}{g} \sqrt{\frac{9 η v}{2 ρ g}}$

Examiner Tip

"Show that" questions are one of the rare moments in an exam you can be totally confident you have the correct answer, but don't get complacent. The marks are awarded for clear and logical working out. Don't try to skip a step and hope you can convince your examiner, be thorough.

Stokes' Law (AQA A Level Physics)

Revision Note