Specific Charge Experiments | AQA A Level Physics Revision Notes 2017

Determining the Specific Charge of an Electron

Specific charge is the charge per unit mass of an object - this has units of C kg^-1
- For an electron, this is $\frac{e}{m_{e}}$ , where e is the charge of an electron and m_e is the mass of an electron
You need to be able to describe how specific charge is determined using:
- A magnetic field only
- A magnetic field and an electric field
- An electric field only

Determining Specific Charge with A Magnetic Field Only

When moving in a magnetic field, a charge experiences a force perpendicular to its motion

Electron beam in a magnetic field

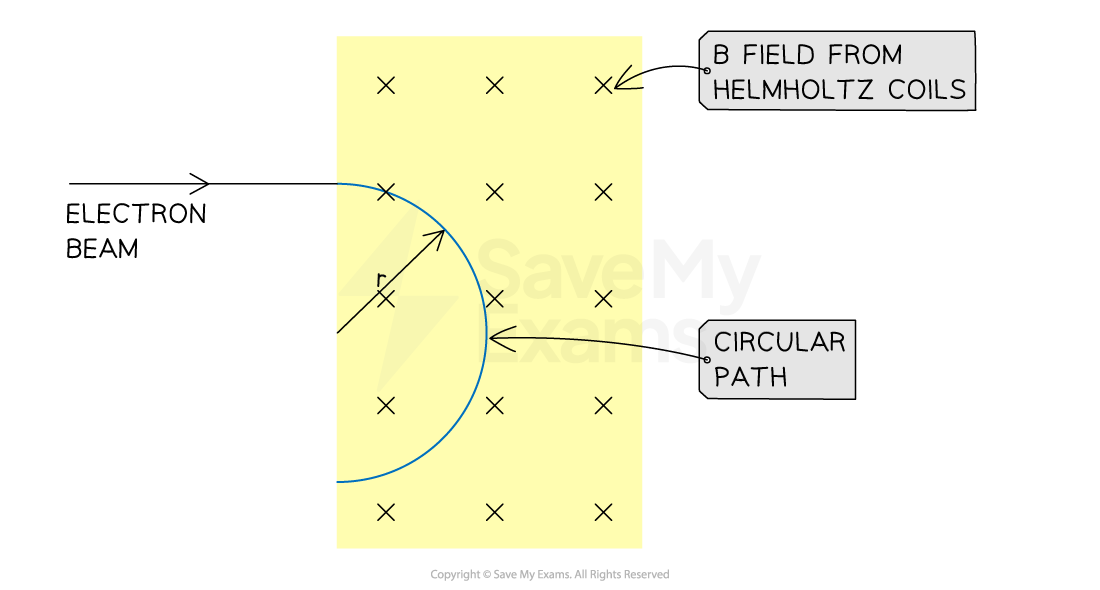
12-1-3-circular-path

The radius of the electron beam's circular path can be measured to calculate specific charge

Recall for a circular path of radius r with electrons of mass m_emoving at a speed v, the centripetal force F is:

$F = \frac{m_{e} v^{2}}{r}$

For a magnetic force, F_B, from a field with flux density B on a charge of magnitude e :

$F_{B} = B e v$

This magnetic force is the centripetal force so we can equate the two equations above and write as an expression for v :

$B e v = \frac{m_{e} v^{2}}{r}$

$v = \frac{B e r}{m_{e}}$

Recall from Thermionic Emission that work done on electrons by an anode of potential difference V_A can be equated to their kinetic energy:

$e V_{A} = \frac{1}{2} m_{e} v^{2}$

By substituting the expression for speed from above, we can determine the specific charge (try deriving this yourself):

$\frac{e}{m_{e}} = \frac{2 V_{A}}{B^{2} r^{2}}$

The terms V_A, r, and B can all be measured, so this experiment allows the specific charge of the electron to be determined

Balancing Electric and Magnetic Fields - J.J. Thomson's Method

To determine the specific charge of an electron, J.J. Thomson balanced magnetic and electric forces on a beam of electrons
- A piece of apparatus called Helmholtz coils generates a magnetic field
- Oppositely charged plates generate an electric field

A diagram showing the balanced forces from Helmholtz coils and an electric field

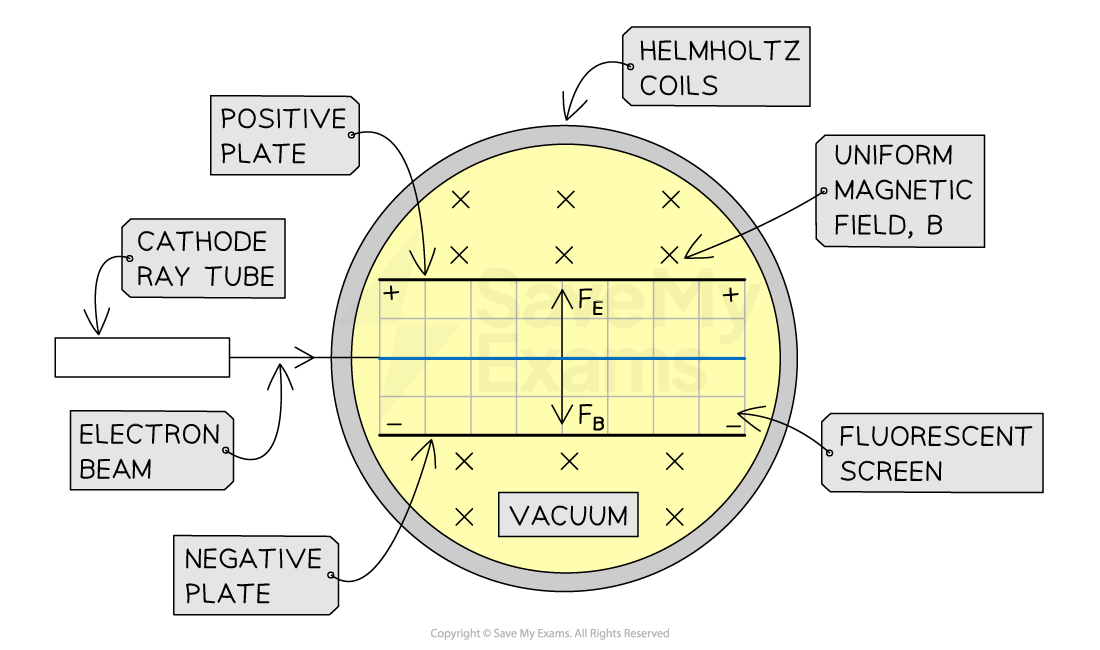
12-1-3-helmholtz

The magnetic field generates a downward force, the electric field between the plates generates an upward force - the fluorescent screen shows a straight beam when these two forces are equal and opposite

In this diagram, the Helmholtz coils' magnetic field points into the plane of the page, exerting a downward magnetic force F_B (you can verify this with the left-hand rule)
The electric field strength, E, can be varied by changing the potential difference V across the plates (separated by distance d ) until the electric force, F_E, is equal to F_B:

$F_{E} = F_{B}$

Recall that the force from the electric field can be calculated using the charge on the electron, e :

$F_{E} = e E = \frac{e V}{d}$

For magnetic flux density B and electron velocity v, magnetic force is:

$F_{B} = B e v$

Equating the two forces allows us to determine electron speed:

$B e v = \frac{e V}{d}$

$v = \frac{V}{B d}$

The electric field was then switched off, and the beam formed a circular path, allowing the equation from the magnetic field only method to be used:

$v = \frac{B e r}{m_{e}}$

Combining these two equations gave Thomson the expression:

$\frac{e}{m_{e}} = \frac{V}{r B^{2} d}$

The terms V , r , B and d can all be measured, so this experiment allowed the specific charge of the electron to be determined

Specific Charge using an Electric Field Only

This method uses constant acceleration equations for the beam of electrons passing through an electric field

Trajectory of electron beam in electric field

12-1-3-electric-field

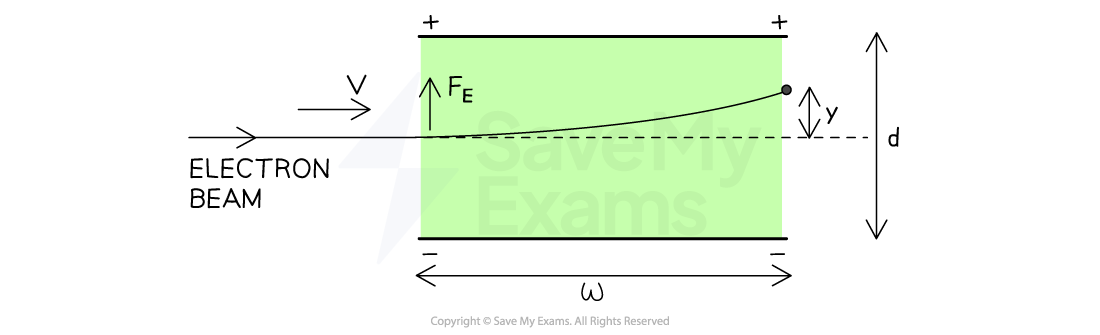
The horizontal speed of the electrons remain constant, but they have a constant acceleration vertically

This can be treated like a standard trajectory problem - time t of the path is calculated using the horizontal speed v and width of the plates w :

$t = \frac{w}{v}$

Now considering the vertical plane, the upwards acceleration a can be calculated using F = ma :

$a = \frac{F_{E}}{m_{e}} = \frac{e V}{d m_{e}}$

Constant acceleration equations can also be used in the vertical plane for another expression for acceleration:

$s = u t + \frac{1}{2} a t^{2}$

- Initial velocity is 0 ms⁻¹ vertically, therefore ut = 0
- Displacement, s, can be measured (see y on the diagram)
- Time,t, is given by the first expression above
- Therefore:

$y = \frac{1}{2} a \frac{w^{2}}{v^{2}}$

Speed can be calculated by equating work done and kinetic energy, as in the magnetic field method, and acceleration can be calculated once y and w are measured
- This means specific charge can once again be determined if we rearrange this expression for a :

$a = \frac{e V}{d m_{e}}$

- To give:

$\frac{e}{m_{e}} = \frac{a d}{V}$

Worked example

A group of students are unsure of the magnetic flux density generated by an old set of Helmholtz coils from their school.

Using a pair of charged plates of known separation with a known potential difference across them and the Helmholtz coils, they form a straight beam coming from an electron gun. They do not know the potential difference across the electron gun.

Their teacher reminds them of the following equations:

$specific charge of an electron = \frac{v}{r B}$

$v = \frac{V}{B d}$

Their teacher also reminds them of their AQA data booklets.

Explain what else they must do to determine the magnetic flux density of the Helmholtz coils.

Answer:

Step 1: List the quantities the students know

The students know:
- Potential difference, V
- Separation of the plates, d
The students need to find the term B

Step 2: Describe how the students can determine the missing quantities

The students need the radius r of the electron beam in the electric field
They can turn off the electric field and measure the radius of the circular path of the electrons
Specific charge of an electron is the magnitude of an electron's charge divided by its mass
Both quantities can be found in their data booklets

Step 3: Explain how they can use this to determine B

The students must now rearrange the given equations to make B the subject and substitute their values

Examiner Tip

You must be prepared to answer questions and perform calculations on all three methods, but you only need to be able to recall the method for one of the three methods. The magnetic field method has appeared regularly in past papers so this may be a sensible choice.

Specific Charge Experiments (AQA A Level Physics)

Revision Note

Determining the Specific Charge of an Electron

Determining Specific Charge with A Magnetic Field Only

Electron beam in a magnetic field

Balancing Electric and Magnetic Fields - J.J. Thomson's Method

A diagram showing the balanced forces from Helmholtz coils and an electric field

Specific Charge using an Electric Field Only

Trajectory of electron beam in electric field

Worked example

Examiner Tip

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan MG