Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsThermodynamics & EnginesPower Output of an Engine

Power Output of an Engine (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Power Output of an Engine

  • An engine's efficiency depends on its power output

  • This is determined by the fuel

Input Power

  • The calorific value of fuel is the amount of energy fuel stores per unit volume (or per unit mass)

    • For liquid fuel, this is measured in J kg–1

    • For a gas, this is measured in J m–3

  • The flow rate of fuel is the volume (or mass) that flows per second

    • For liquid fuel, this is measured in kg s–1

    • For a gas, this is measured in m3 s–1

  • The product of these gives the input power of the engine:

I n p u t space p o w e r space equals space c a l o r i f i c space v a l u e space cross times space f u e l space f l o w space r a t e

Indicated Power

  • The indicated power is the power developed in the cylinder of an engine

  • This depends on the number of cycles (strokes) per second

N u m b e r space o f space c y c l e s space p e r space s e c o n d space equals space fraction numerator 1 over denominator t i m e space f o r space o n e space c y c l e end fraction

  • In a four-stroke engine, 1 cycle is equal to 2 revolutions 

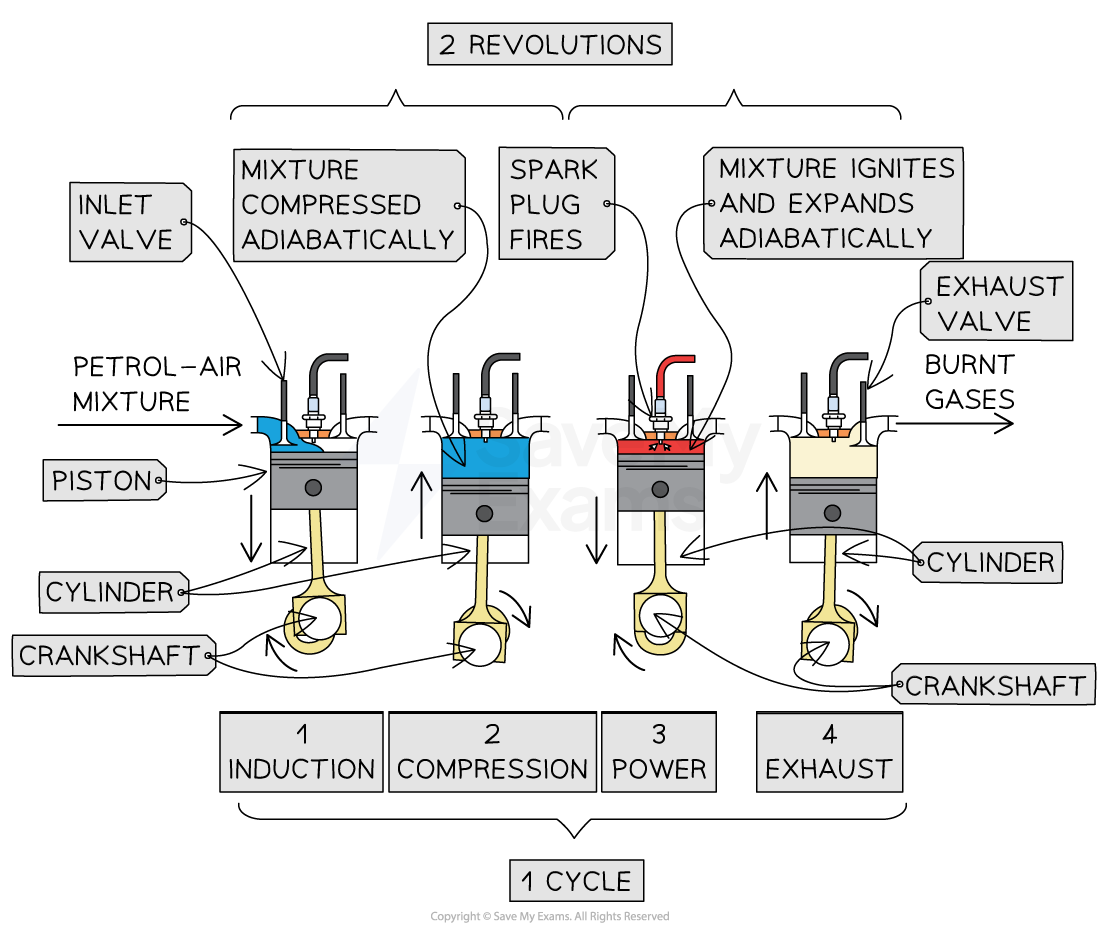
11-2-7-revolutions-and-cycles

A four-stroke engine has 2 revolutions of the crankshaft in one cycle

  • The power developed is the work done each second, which is the area of the main p-V  loop of the indicator diagram

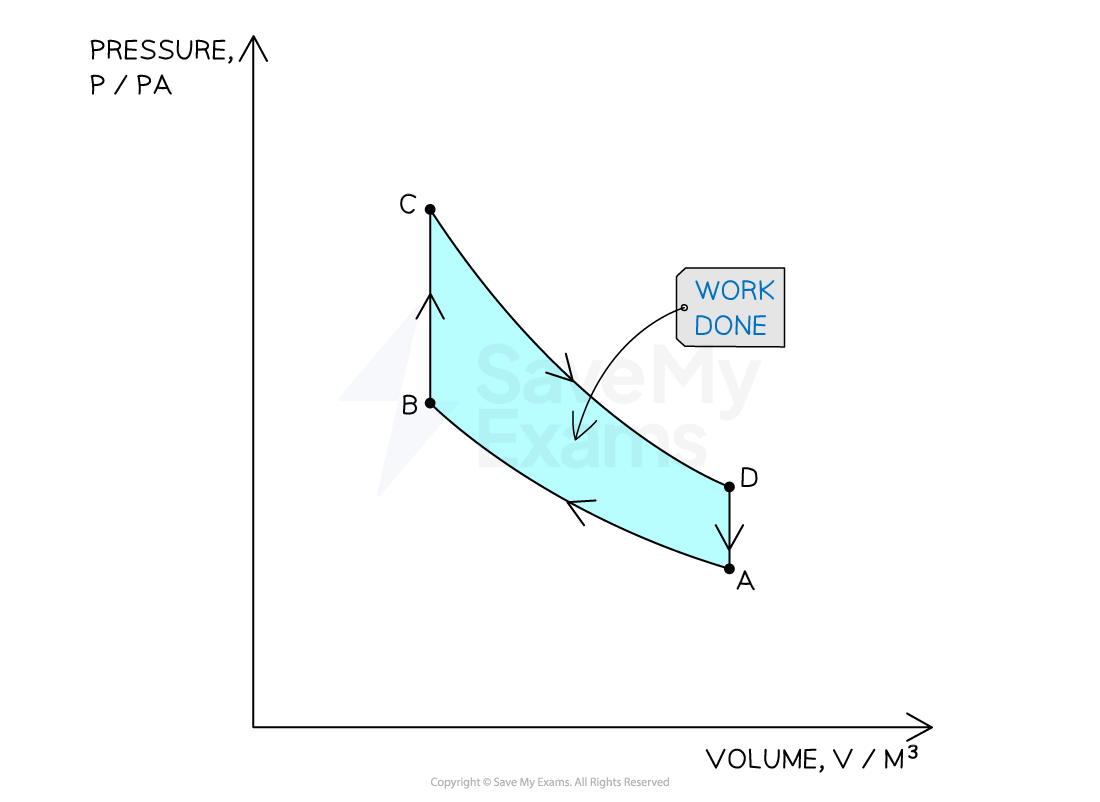
11-2-7-work-done-area

Area of p–V loop for a diesel engine

  • The indicated power is defined by the equation:I n d i c a t e d space p o w e r space equals space open parentheses a r e a space o f space p minus V space l o o p close parentheses space cross times space open parentheses n u m b e r space o f space c y c l e s space p e r space s e c o n d close parentheses space cross times space open parentheses n u m b e r space o f space c y l i n d e r s space i n space e n g i n e close parentheses

Output (Brake) Power

  • The brake power is the power output by the engine and is the same as the rotational power

P space equals space T omega

Friction Power

  • Part of the indicated power must be used to overcome frictional forces within the engine

    • Due to this, this means the brake power is lower than the indicated power

  • It is defined as: 

    F r i c t i o n space p o w e r space equals space i n d i c a t e d space p o w e r space minus space b r a k e space p o w e r

Worked Example

A four-stroke diesel engine with three cylinders is running at constant speed on a test bed. An indicator diagram for one cylinder is shown in the figure below and other test data are given below: 

  • measured output power of engine (brake power) = 75.0 kW

  • fuel used in 150 seconds = 0.284 litre

  • calorific value of fuel = 38.6 MJ litre–1

  • engine speed = 3500 rev min–1

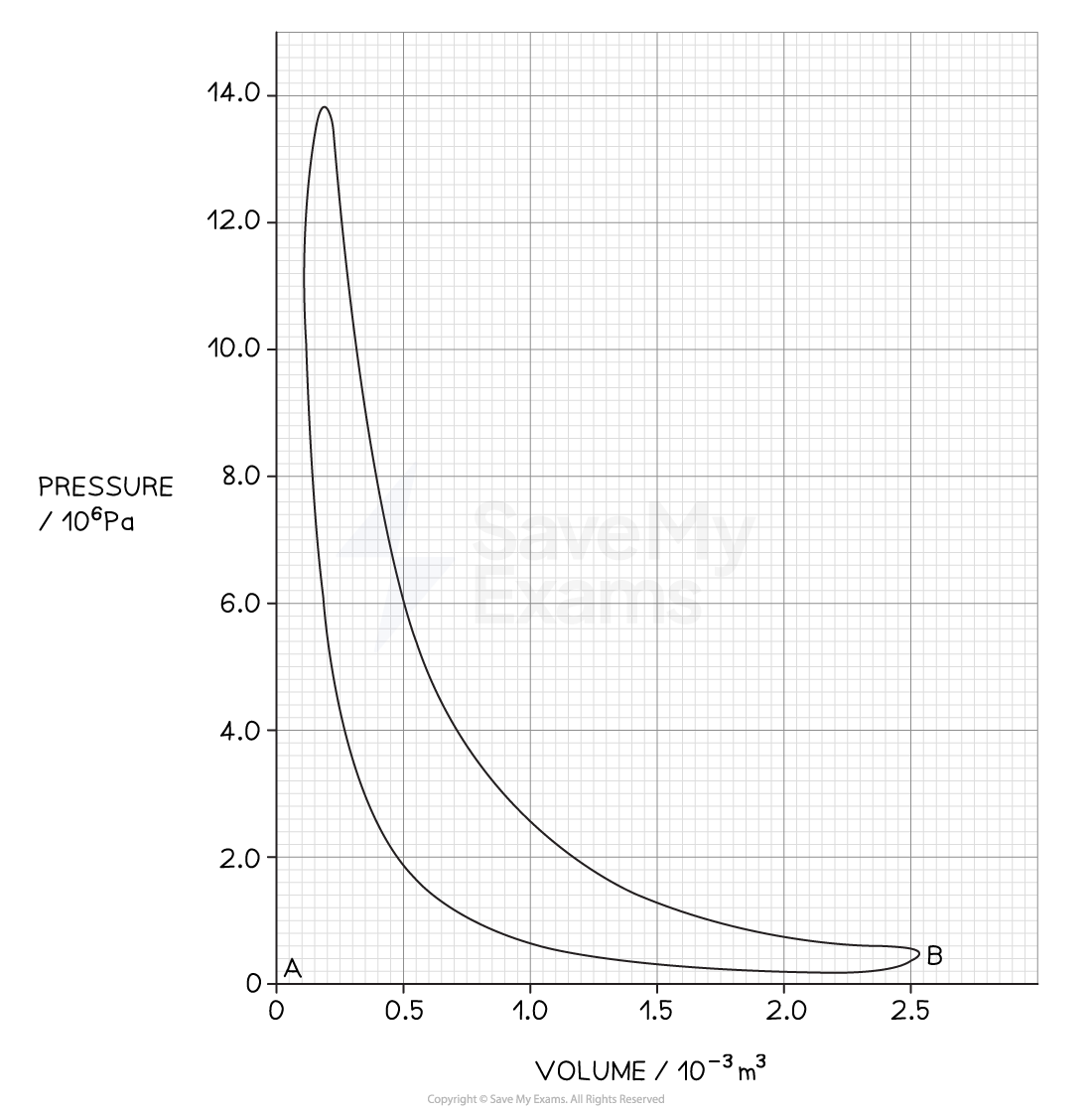
11-2-7-p-v-diagram-we

(a) Determine the indicated power of the engine, assuming all cylinders give the same power

 (b) Calculate the input power of the engine.

Answer

Part (a)

Step 1: State the indicated power equation

I n d i c a t e d space p o w e r space equals space open parentheses a r e a space o f space p minus V space l o o p close parentheses space cross times space open parentheses n u m b e r space o f space c y c l e s space p e r space s e c o n d close parentheses space cross times space open parentheses n u m b e r space o f space c y l i n d e r s close parentheses

Step 2: Calculate the number of cycles per second

  • The engine speed is 3500 rev min–1

    • This is 3500 over 60 rev s–1

    • 1 cycle = 2 revolutions

    • Therefore, the number of cycles per second is

open parentheses 3500 over 60 close parentheses space cross times space 1 half

Step 3: Calculate the area of the p-V loop

  • It is easier to use the big squares

  • 1 big square = volume of (0.5 × 10–3) × (2.0 × 106) = 1000 m3 Pa

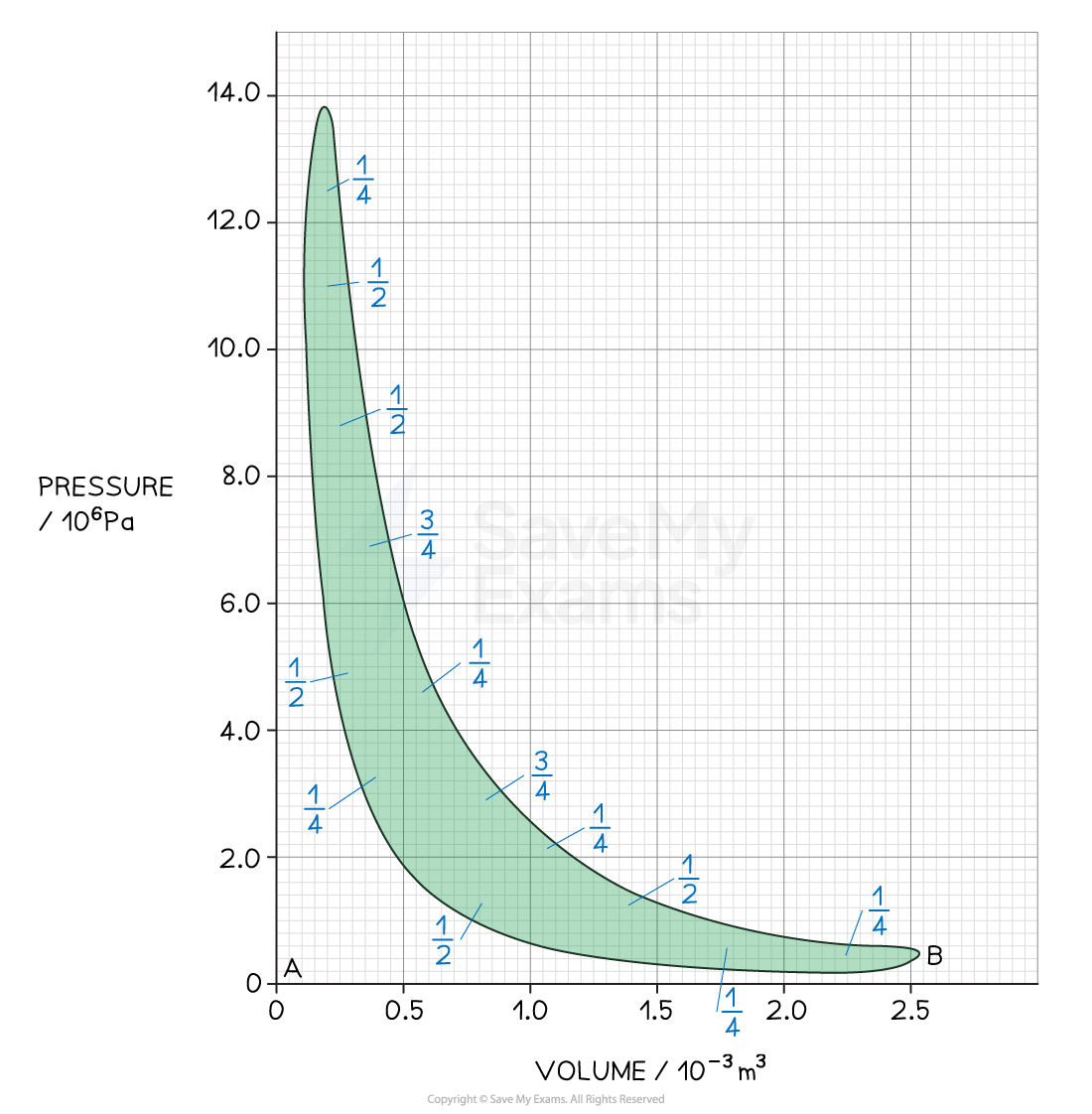
11-2-7-p-v-diagram-solution

  • Splitting up the graph into squares gives

open parentheses 6 space cross times fraction numerator space 1 over denominator 4 end fraction close parentheses space plus space open parentheses 5 space cross times 1 half close parentheses space plus thin space open parentheses 2 space cross times 1 fourth close parentheses space equals space 4.5 squares

  • This gives an area of 

4.5 space cross times space 1000 space equals space 4500 space

  • The indicated power is therefore:

I n d i c a t e d space p o w e r space equals space 4500 space cross times space open parentheses 3500 over 60 space cross times 1 half close parentheses space cross times space 3 space equals space 394 space kW

Part (b)

Step 1: State the input power equation

I n p u t space p o w e r space equals space c a l o r i f i c space v a l u e space cross times space f u e l space f l o w space r a t e

Step 2: Calculate the fuel rate

  • Fuel used in 150 seconds = 0.284 litres

F u e l space r a t e space equals fraction numerator space 0.284 over denominator 150 end fraction space equals space 0.0019 space litres space straight s to the power of negative 1 end exponent

Step 3: Calculate the input power

I n p u t space p o w e r space space equals space open parentheses 38.6 space cross times space 10 to the power of 6 close parentheses space cross times space 0.0019 space equals space 73340 space equals space 7.3 space cross times space 10 to the power of 4 space straight W

Examiner Tips and Tricks

There are a lot of equations here. These are all given in your data sheet, so you must be confident with how to use them.

For input power, make sure the calorific value and flow rate are in the same units. For example, if one is in terms of mass, the other must also be in terms of mass.

Sometimes, the engine may not have cylinders. Not all engines will require cylinders to function, depending on their type. In this case, this part of the indicated power equation can be omitted. Make sure you use the number of cycles per second instead of the time for one cycle!

Being able to find areas from graphs by counting the squares is a very important skill to have in A level physics. The mark scheme will allow a wide range of answers, so don't worry if you're approximations are slightly out, as the accepted answers will adjust for these

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Comparing Petrol & Diesel EnginesNext:Engine Efficiency
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.