Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsThermodynamics & EnginesThermodynamic Processes

Thermodynamic Processes (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Thermodynamic Processes

  • The four main thermodynamic processes are

    • Constant volume open parentheses W space equals space 0 close parentheses

    • Constant pressure open parentheses increment p space equals space 0 close parentheses

    • Isothermal open parentheses increment T space equals space 0 close parentheses

    • Adiabatic open parentheses increment Q space equals space 0 close parentheses

Constant pressure

  • An isobaric (constant pressure) process is defined as:

    A process in which no change in pressure occurs

  • This occurs when gases are allowed to expand or contract freely during a change in temperature

  • When there is a change in volume ΔV at a constant pressure p, work done W is equal to

W space equals space p increment V

  • From the first law of thermodynamics:

Q space equals space increment U space space plus space W

Q space equals space increment U space space plus-or-minus thin space p increment V

  • The ± sign reflects whether work has been done on or by the gas as a result of the change in volume

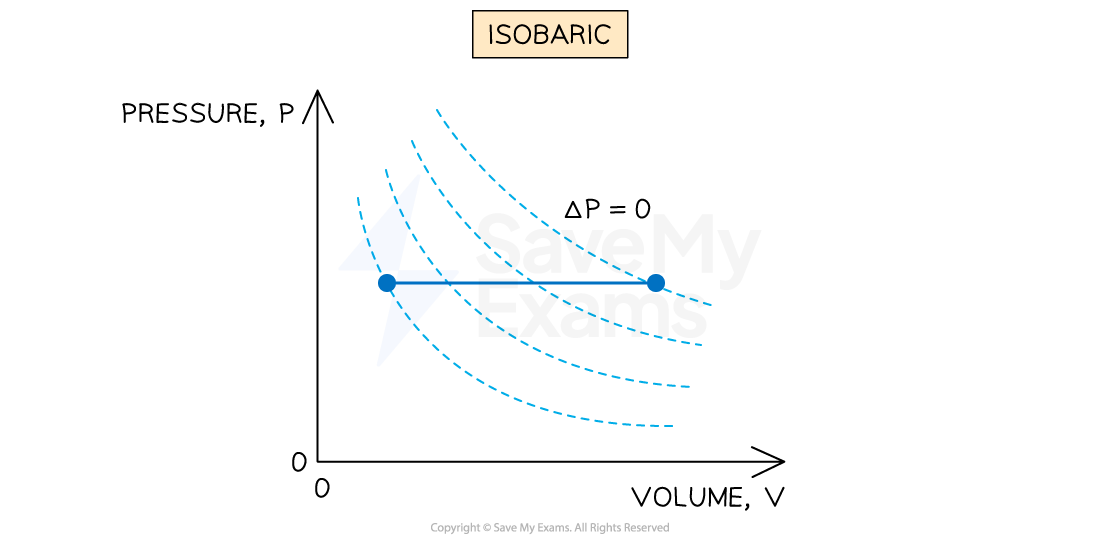
2-4-6-isobaric-pv-diagram

The solid blue line represents an isobaric process at constant pressure on a p-V diagram

Constant volume

  • An isovolumetric (constant volume) process is defined as:

    A process where no change in volume occurs and the system does no work

  • If there is no change in volume, then there is no work done on or by the gas, so W space equals space 0

  • Therefore, from the first law of thermodynamics:

Q space equals space increment U space space plus space W space equals space increment U space space plus space 0

Q space equals space increment U 

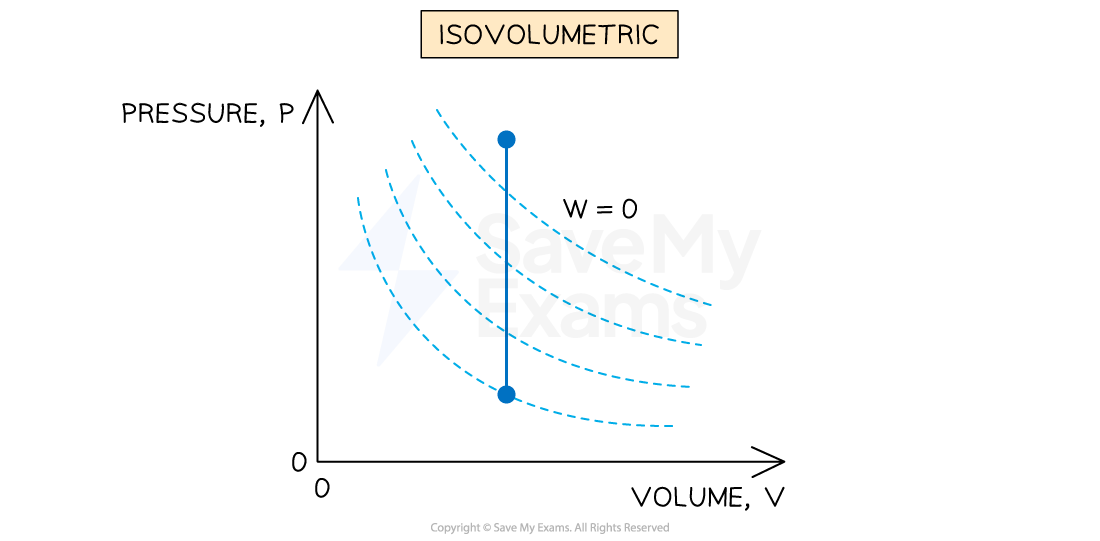
2-4-6-isovolumetric-pv-diagram

The solid blue line represents an isovolumetric process at constant volume on a p-V diagram

Constant temperature (isothermal)

  • An isothermal process is defined as:

    A process in which no change in temperature occurs

  • If the temperature does not change, then the internal energy of the gas will not change, so increment U space equals space 0

  • Therefore, from the first law of thermodynamics:

Q space equals space increment U space space plus space W space equals space 0 space plus thin space W

Q space equals space W

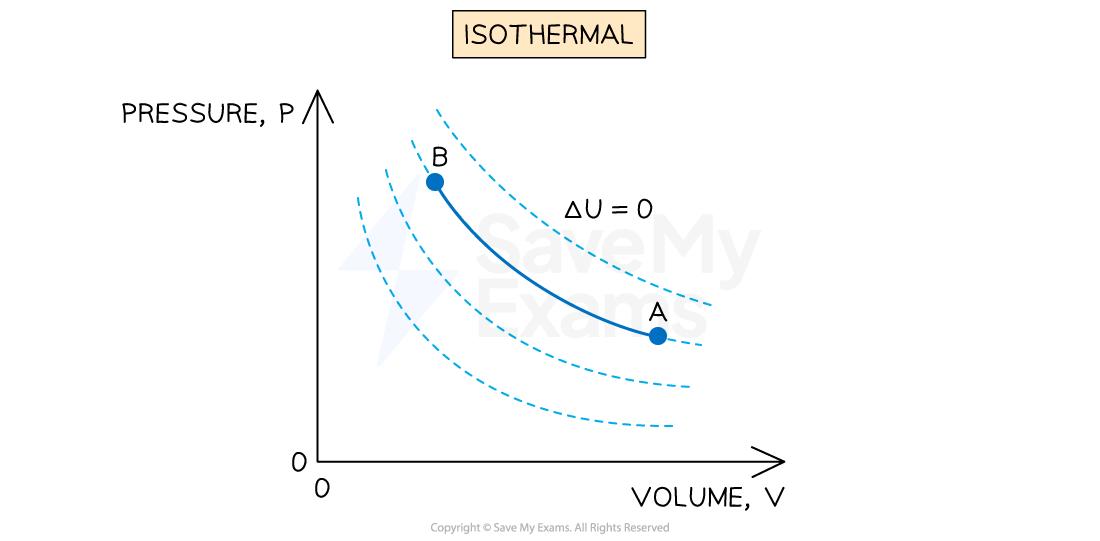
2-4-6-isothermal-pv-diagram

The solid blue line represents an isothermal process with constant temperature on a p-V diagram

Constant thermal energy (adiabatic)

  • An adiabatic process is defined as:

    A process where no heat is transferred into or out of the system

  • If there is no heat entering or leaving the system then Q space equals space 0

  • Therefore, from the first law of thermodynamics:

Q space equals space increment U space space plus space W space equals space 0

W space equals space minus increment U space

  • This means that all the work done is at the expense of the system's internal energy

  • Hence, an adiabatic process will usually be accompanied by a change in temperature

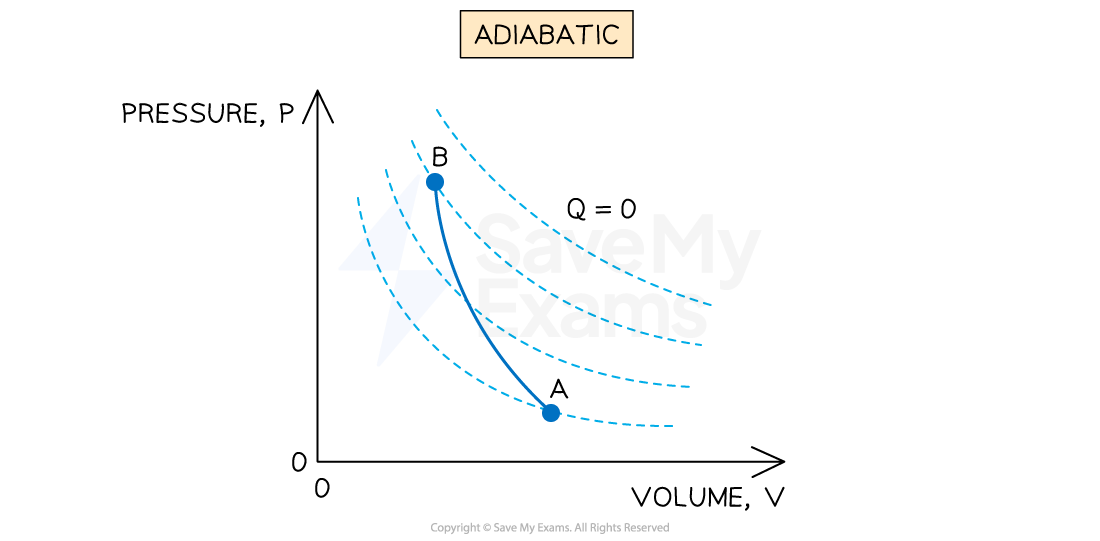
2-4-6-adiabatic-pv-diagram

The solid blue line represents an adiabatic process with constant thermal energy on a p-V diagram

Adiabatic Processes

  • Adiabatic processes in ideal gases can be modelled by the equation

space p V to the power of gamma space equals space c o n s t a n t

  • Where:

    • p = pressure of the gas (Pa)

    • V = volume occupied by the gas (m3)

  • This equation can be used for calculating changes in pressure, volume and temperature, e.g. for monatomic ideal gases, where gamma space equals space 5 over 3

space p subscript 1 V subscript 1 to the power of 5 over 3 end exponent space equals space p subscript 2 V subscript 2 to the power of 5 over 3 end exponent

  • Where:

    • space p subscript 1 = initial pressure (Pa)

    • space p subscript 2 = final pressure (Pa)

    • V subscript 1 = initial volume (m3)

    • V subscript 2 = final volume (m3)

Worked Example

A quantity of energy Q is supplied to three ideal gases X, Y and Z.

Gas X absorbs Q isothermally, gas Y isovolumetrically and gas Z isobarically.

Complete the table by inserting the words ‘positive’, ‘zero’ or ‘negative’ for the work done W, the change in internal energy ΔU and the temperature change ΔT for each gas.

 

W

increment U

increment T

X

 

 

 

Y

 

 

 

Z

 

 

 

Answer:

  • X: Isothermal = constant temperature, no change in internal energy

    • Temperature:  increment T space equals space 0

    • Internal energy:  increment T space proportional to space increment U, so, increment U space equals space 0

    • Work done:  Q space equals space increment U space space plus space W space space space space space rightwards double arrow space space space space space Q space equals space plus W

  • Y: Isovolumetric = constant volume, no work done

    • Work done:  W space proportional to space increment V, so, W space equals space 0

    • Internal energy:  Q space equals space increment U space space plus space W space space space space space rightwards double arrow space space space space space Q space equals space plus increment U

    • Temperature:  increment T space proportional to space increment U, so, increment T space greater than space 0

  • Z: Isobaric = constant pressure 

    • Work done:  increment p space equals space 0, so W space equals space p increment V, so W space greater than space 0

    • Internal energy:  Q space equals space increment U space space plus space W, so increment U space greater than space 0

    • Temperature:  increment T space proportional to space increment U, so increment T space greater than space 0

 

W

increment U

increment T

X

positive

0

0

Y

0

positive

positive

Z

positive

positive

positive

Worked Example

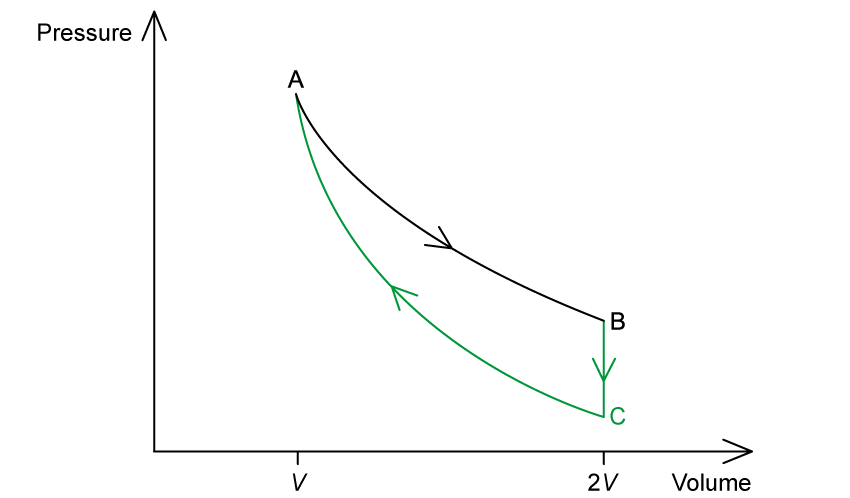
A heat engine operates on the cycle shown in the pressure-volume diagram. One step in the cycle consists of an isothermal expansion of an ideal gas from state A of volume V to state B of volume 2V.  

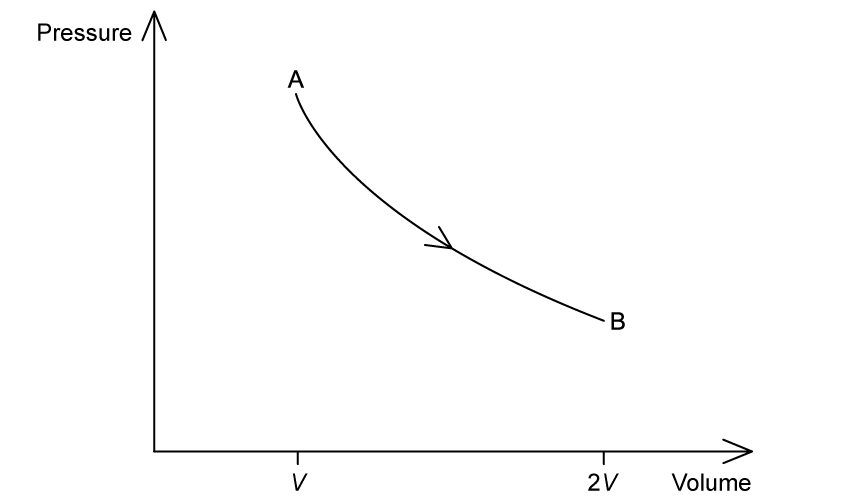
2-4-6-entropy-in-a-heat-engine-worked-example

On the graph, complete the cycle ABCA by drawing curves to show

  • a change at constant volume from state B to state C

  • an adiabatic compression from state C to state A

Answer:

  • Constant volume = no work done

  • Next step is a compression (where pressure increases), so this step should involve a pressure drop 

    • Hence, B to C: line drawn vertically down

  • Adiabatic = no heat supplied or removed, compression = work is done on the gas, volume decreases

    • Hence, C to A: line curves up to meet A

2-4-6-entropy-in-a-heat-engine-worked-example-ma

Worked Example

An ideal monatomic gas open parentheses gamma space equals space 5 over 3 close parentheses expands adiabatically from a state with pressure 7.5 × 105 Pa and volume 1.8 × 10−3 m3 to a state of volume 4.2 × 10−3 m3.

Calculate the new pressure of the gas.

Answer:

  • For an ideal monatomic gas undergoing an adiabatic change:

space p V to the power of 5 over 3 end exponent space equals space C

space p subscript 1 V subscript 1 to the power of 5 over 3 end exponent space equals space p subscript 2 V subscript 2 to the power of 5 over 3 end exponent

  • Where:

    • Initial pressure, space p subscript 1 = 7.5 × 105 Pa

    • Final pressure =space p subscript 2

    • Initial volume, V subscript 1 = 1.8 × 10−3 m3 

    • Final volume, V subscript 2 = 4.2 × 10−3 m3

space p subscript 2 space equals space p subscript 1 space open parentheses V subscript 1 over V subscript 2 close parentheses to the power of 5 over 3 end exponent

space p subscript 2 space equals space open parentheses 7.5 cross times 10 to the power of 5 close parentheses space cross times space open parentheses fraction numerator 1.8 cross times 10 to the power of negative 3 end exponent over denominator 4.2 cross times 10 to the power of negative 3 end exponent end fraction close parentheses to the power of 5 over 3 end exponent

New pressure: space p subscript 2 = 1.8 × 105 Pa

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:p–V DiagramsNext:Petrol Engine Cycle
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.