Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsThermodynamics & EnginesHeat Engines

Heat Engines (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Efficiency of a Heat Engine

  • The goal of a heat engine is to transfer thermal energy into useful mechanical work as efficiently as possible

  • The efficiency of a heat engine can, therefore, be calculated using

efficiency equals fraction numerator u s e f u l italic space w o r k italic space o u t p u t over denominator t o t a l italic space e n e r g y italic space i n p u t end fraction

efficiency equals W over Q subscript H space equals space fraction numerator Q subscript H minus Q subscript C over denominator Q subscript H end fraction

  • Where:

    • W = useful work output (J)

    • QH = energy transferred from the source (J)

    • QC = energy transferred to the sink (J)

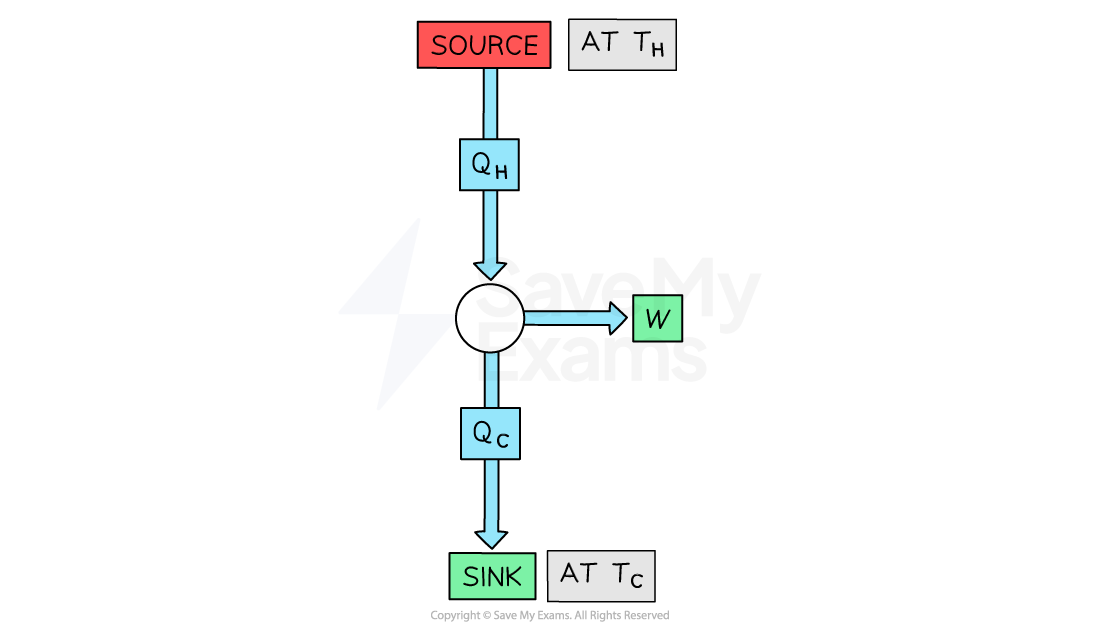
11-2-9-heat-engine

Source-sink diagram for a heat engine

  • Since the efficiency of a heat engine can never be 0 (otherwise there would no work!) this means no heat engine can completely convert heat into work

Worked Example

Which is a correct statement about an ideal heat engine?

A. The efficiency is 75% when the kelvin temperature of the hot source is four times the kelvin temperature of the cold sink

B. The maximum efficiency depends on the p-V cycle of the engine

C. The efficiency is decreased when the kelvin temperature of the hot source and the cold sink are decreased by equal amounts

D. The efficiency is 25% when the kelvin temperature of the hot source is four times the kelvin temperature of the cold sink

Answer: A

  • If the hot source is four times the kelvin temperature of the cold sink, then Q subscript H space equals space 4 Q subscript C space

  • In the efficiency equation, this is

fraction numerator Q subscript H space minus space Q subscript C over denominator Q subscript H end fraction space equals space fraction numerator 4 Q subscript C space minus space Q subscript C over denominator 4 Q subscript C end fraction space equals space fraction numerator 3 Q subscript C over denominator 4 Q subscript C end fraction space equals 3 over 4 space equals space 0.75

  • This efficiency is 75 %

Examiner Tips and Tricks

This equation is given on your data sheet. Make sure all the variables are in the same units i.e. J or kJ. You must convert these into the same units before you do your calculation. 

If the efficiency is asked for as a percentage instead of a decimal, remember to × 100

Maximum Theoretical Efficiency

  • As the efficiency of a thermodynamic system increases, the difference between the temperatures of the source and sink increases

  • The maximum theoretical efficiency of a heat engine is:

Maximum theoretical efficiency = fraction numerator T subscript H space minus space T subscript C over denominator T subscript H end fraction

  • Where:

    • T subscript C = temperature in the sink (cold reservoir) (K)

    • T subscript H = temperature in the source (hot reservoir) (K)

  • This equation can be used if an ideal gas is used as a substance for the engine

  • Therefore, to make an engine as efficient as possible, the source temperature must be as high as possible, and the sink temperature as low as possible

  • The maximum theoretical efficiency is 100% only if the sink temperature is at 0 K

Worked Example

An engineer designs a heat engine that has an inlet temperature of 500 K and an outlet temperature of 300 K. The engineer claims that 100 kJ of thermal energy flows out of the source and 25 kJ of thermal energy flows into the sink.

Determine, with reference to the second law of thermodynamics, whether this engine is thermodynamically possible.

Answer:

Step 1: Determine the efficiency of the proposed engine

  • The efficiency of this engine would be

e f f i c i e n c y space equals space W over Q subscript H space equals space fraction numerator Q subscript H space minus space Q subscript C over denominator Q subscript H end fraction

  • Where:

    • Heat transferred in, Q subscript H = 100 kJ

    • Heat transferred out, Q subscript C = 25 kJ

Efficiency = fraction numerator 100 space minus space 25 over denominator 100 end fraction = 0.75 = 75%

Step 2: Determine the maximum theoretical efficiency of the proposed engine

  • A Carnot engine operating between the same temperatures would have an efficiency of

Maximum theoretical efficiency = fraction numerator T subscript H space minus space T subscript C over denominator T subscript H end fraction

  • Where:

    • Inlet temperature, T subscript H = 500 K

    • Outlet temperature, T subscript C = 300 K

Maximum theoretical efficiency =  fraction numerator 500 space minus space 300 over denominator 500 end fraction = 0.4 = 40%

Step 3: Discuss the proposed engine in relation to the second law

  • The second law of thermodynamics states that it is impossible for heat to flow from a cooler body to a hotter body without performing work

  • This law sets an upper limit on the maximum possible efficiency of the transfer of thermal energy to mechanical energy in a heat engine

  • The maximum possible efficiency of the proposed engine is 40%, but the engineer is proposing an efficiency of 75% i.e. an efficiency greater than the efficiency of the engine

  • This violates the second law, hence the proposed engine is impossible

Examiner Tips and Tricks

This equation is valid for all idealised reversible engines, irrespective of the particular cycle and the particular working substance. You may be given unfamiliar cycles in the exam (such as the Carnot cycle) to apply this to.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Second Law of ThermodynamicsNext:Limitations of Real Heat Engines
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.