Revision NotesExam QuestionsPast PapersMock Exams
A LevelPhysicsAQARevision NotesEngineering PhysicsRotational DynamicsRotational Kinetic Energy

Rotational Kinetic Energy (AQA A Level Physics): Revision Note

Exam code: 7408

Ashika

Author

Ashika

Last updated

Rotational Kinetic Energy

  • A body moving with linear velocity has an associated linear kinetic energy given by

E subscript k space equals space 1 half m v squared

E subscript k space equals space fraction numerator p squared over denominator 2 m end fraction

  • Similarly, a rotating body with angular velocity has an associated rotational kinetic energy given by

E subscript k space equals space 1 half I omega squared

E subscript k space equals space fraction numerator L squared over denominator 2 I end fraction

  • Where:

    • E subscript k = rotational kinetic energy (J)

    • I = moment of inertia (kg m2)

    • omega = angular velocity (rad s−1)

    • L = angular momentum (kg m2 s−1)

Rolling without slipping

  • Circular objects, such as wheels, are made to move with both linear and rotational motion

    • For example, the wheels of a car, or bicycle rotate causing it to move forward

  • Rolling motion without slipping is a combination of rotating and sliding (translational) motion

  • When a disc rotates:

    • Each point on the disc has a different linear velocity depending on its distance from the centre open parentheses v space proportional to space r close parentheses

    • The linear velocity is the same at all points on the circumference 

  • When a disc slips, or slides:

    • There is not enough friction present to allow the object to roll

    • Each point on the object has the same linear velocity

    • The angular velocity is zero

  • So, when a disc rolls without slipping:

    • There is enough friction present to initiate rotational motion allowing the object to roll

    • The point in contact with the surface has a velocity of zero

    • The centre of mass has a velocity of v space equals space omega r

    • The top point has a velocity of 2 v or 2 omega r

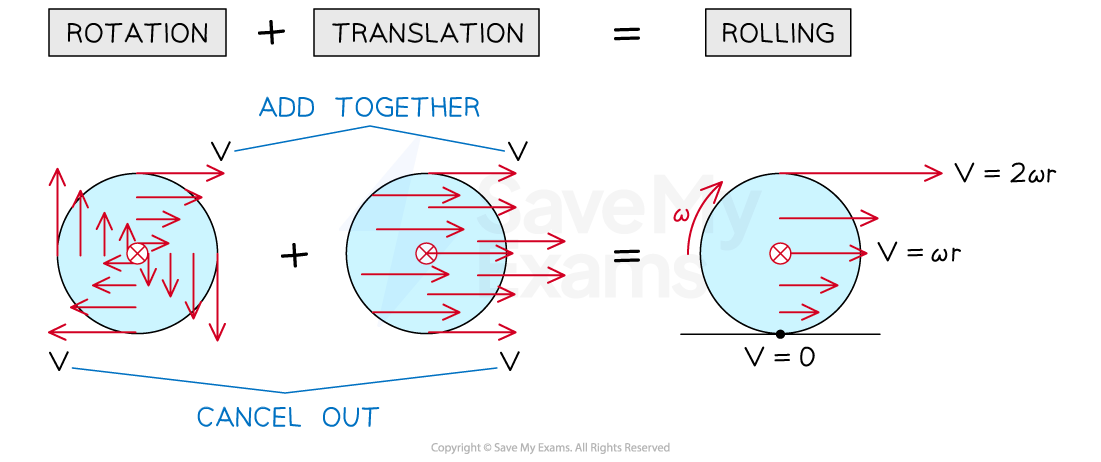
E16CHGH6_1-4-9-rotational-kinetic-energy-rolling-without-slipping

Rolling motion is a combination of rotational and translational motion. The resultant velocity at the bottom is zero and the resultant velocity at the top is 2v

Rolling down a slope

  • Another common scenario involving rotational and translational motion is an object (usually a ball or a disc) rolling down a slope

  • At the top of the slope, a stationary object will have gravitational potential energy equal to

E subscript p space equals space m g increment h

  • As the object rolls down the slope, the gravitational potential energy will be transferred to both translational (linear) and rotational kinetic energy

  • At the bottom of the slope, the total kinetic energy of the object will be equal to

E subscript K space t o t a l end subscript space equals space 1 half m v squared space plus space 1 half I omega squared

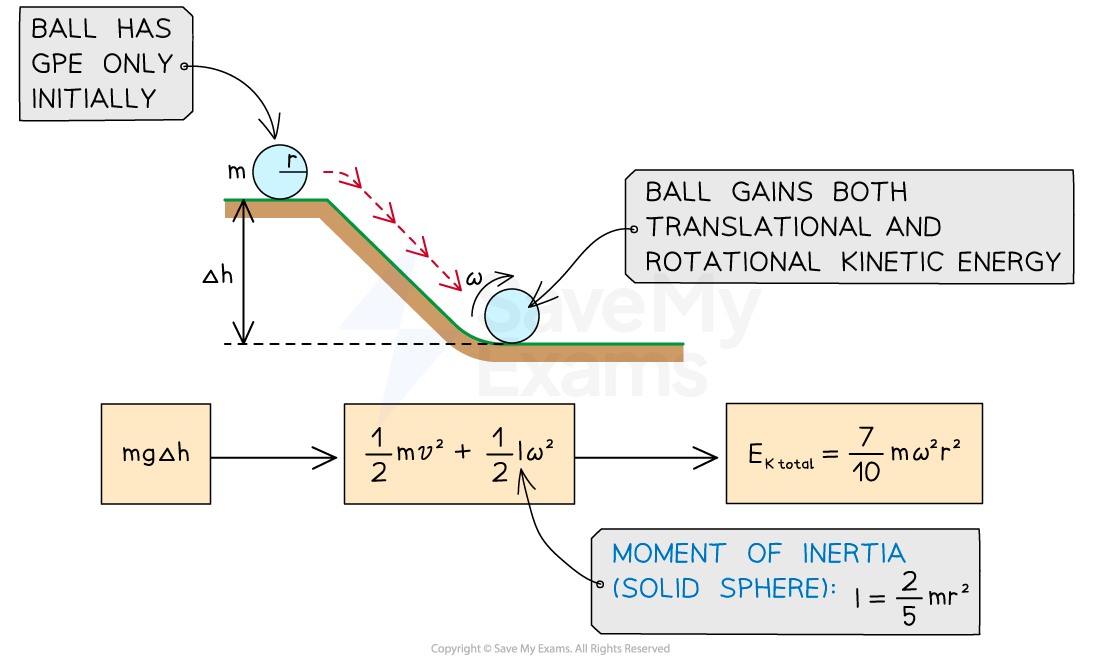
1-4-9-rotational-kinetic-energy-rolling-down-a-slope-ib-2025-physics

The GPE store of the ball is transferred to the translational and rotational kinetic energy store as it rolls down the slope

  • The linear or angular velocity can then be determined by

    • Equating E subscript p and E subscript K space t o t a l end subscript

    • Using the equation for the moment of inertia of the object

    • Using the relationship between linear and angular velocity v space equals space omega r

  • For example, for a ball (a solid sphere) of mass m and radius r, its moment of inertia is

I space equals space 2 over 5 m r squared

  • Equating the equations for E subscript p and E subscript K space t o t a l end subscript and simplifying gives

m g increment h space equals space 1 half m open parentheses omega r close parentheses squared space plus space 1 half open parentheses 2 over 5 m r squared close parentheses omega squared

m g increment h space equals space 1 half m omega squared r squared space plus space 1 fifth m omega squared r squared

m g increment h space equals space 7 over 10 m omega squared r squared

Worked Example

A student conducts an experiment to analyse the rotational motion of a turntable. The diagram shows the turntable with a small lump of gum held above it. An optical sensor connected to a data recorder measures the angular speed of the turntable.

11-1-9-rotational-kinetic-energy-we

The turntable has a mass of 550 g and a radius of 120 mm. It is made to rotate before rotating freely. The lump of gum is dropped from a small height above the turntable and sticks to it. The results from the experiment are as follows:

  • Mass of gum = 9.0 g

  • Distance of gum from the centre of the turntable = 117 mm

  • Angular speed of turntable immediately before gum is dropped = 3.28 rad s–1

The turntable is modelled as a solid disc with a moment of inertia I space equals space 1 half M R squared

Calculate the change in rotational kinetic energy of the system immediately before the gum is dropped until immediately after it sticks to the turntable.

Answer:

Step 1: List the known quantities

  • Initial angular speed, omega subscript i = 3.28 rad s–1

  • Mass of turntable, M = 550 g = 550 × 10−3 kg

  • Radius of turntable, R = 120 mm = 120 × 10−3 m

  • Mass of gum, m = 9.0 g = 9.0 × 10−3 kg

  • Distance of gum from the centre of the turntable, r = 117 mm = 117 × 10−3 m

Step 2: Calculate the moment of inertia of the system before and after the gum is dropped

  • Before the gum is dropped onto the turntable, only the turntable is rotating, so the initial moment of inertia of the system is due to the turntable only

I subscript i space equals space I subscript T space equals space 1 half M R squared space equals space 1 half open parentheses 550 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 120 cross times 10 to the power of negative 3 end exponent close parentheses squared

I subscript i space equals space 3.96 cross times 10 to the power of negative 3 end exponent space kg space straight m squared

  • When the gum is dropped onto the turntable, it can be modelled as a particle at a distance r from the centre of the turntable, with moment of inertia I subscript G space equals space m r squared

  • So the final moment of inertia of the system is due to both the turntable and the gum

I subscript f space equals space open parentheses I subscript T space plus thin space I subscript G close parentheses space equals space open parentheses I subscript T space plus thin space m r squared close parentheses space equals space open parentheses 3.96 cross times 10 to the power of negative 3 end exponent close parentheses space plus thin space open parentheses 9.0 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 117 cross times 10 to the power of negative 3 end exponent close parentheses squared

I subscript f space equals space 4.08 cross times 10 to the power of negative 3 end exponent space kg space straight m squared

Step 3: Determine the kinetic energy of the system before the gum is dropped

  • The gum is initially at rest, so only the turntable has rotational kinetic energy initially

E subscript k comma i end subscript space equals space 1 half I subscript i omega subscript i superscript 2

E subscript k comma i end subscript space equals space 1 half open parentheses 3.96 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 3.28 close parentheses squared space equals space 0.0213 space straight J

Step 4: Apply conservation of angular momentum to determine the final angular speed of the system

  • There is no net torque acting on the system, so the angular momentum of the system is conserved:

I subscript i omega subscript i space equals space I subscript f omega subscript f

omega subscript f space equals space fraction numerator I subscript i omega subscript i over denominator I subscript f end fraction space equals space fraction numerator open parentheses 3.96 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 3.28 close parentheses over denominator 4.08 cross times 10 to the power of negative 3 end exponent end fraction

omega subscript f space equals space 3.184 space rad space straight s to the power of negative 1 end exponent

Step 5: Determine the kinetic energy of the system after the gum is dropped

  • The rotational kinetic energy of the system after the gum has stuck to the turntable is:

E subscript k comma f end subscript space equals space 1 half I subscript f omega subscript f superscript 2

E subscript k comma f end subscript space equals space 1 half open parentheses 4.08 cross times 10 to the power of negative 3 end exponent close parentheses open parentheses 3.184 close parentheses squared space equals space 0.0207 space straight J

Step 6: Calculate the change in the kinetic energy of the system

increment E subscript k space equals space E subscript k comma f end subscript space minus space E subscript k comma i end subscript

increment E subscript k space equals space 0.0207 space minus space 0.0213 space equals space minus 6.0 cross times 10 to the power of negative 4 end exponent space straight J

  • The kinetic energy of the system decreases by 6.0 cross times 10 to the power of negative 4 end exponent space straight J

Examiner Tips and Tricks

Questions with a long calculation like the one in the worked example are best split into sections when putting them into your calculator. This makes it easier to check and type, ensuring the brackets are in the correct place. It is best to type it in exactly as you have it written down so it is input correctly.

The question asks for the change in rotational kinetic energy. This is found by calculating KE after − KE before. You should find that your answer is negative. This is because the gum sticks to the turntable, making it an inelastic collision in which the system's kinetic energy decreases.

Looking at the angular velocity before and after, when it is smaller, tells us that the rotational kinetic energy will also be less. 

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Rotational Work & PowerNext:Flywheels in Machines
    Ashika

    Author: Ashika

    Expertise: Physics Content Creator

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.