Rotational Work & Power (AQA A Level Physics): Revision Note
Exam code: 7408
Work Done & Torque
Work Done by a Rotating Object
Work has to be done on a rigid body when a torque turns in through an angle about an axis
For example, rotating cranes and fairground rides
In systems with linear acceleration, work W is the product of the force and the distance moved
Therefore, the work done for a rotating object is defined by the equation
Where:
W = work done (J)
= torque (N m)
θ = angular displacement (the angle turned through by the rotating object) (rads)
Work can also be calculated by finding the area under a torque-angular displacement graph
Torque-angular displacement graph
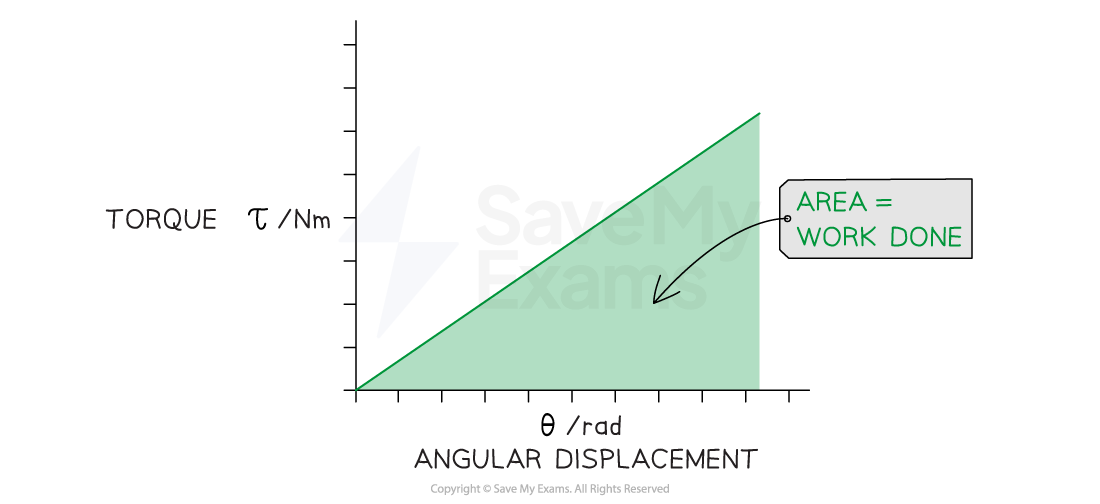
The work done is the area under the torque-angular displacement graph
This is analogous to the work done being the area under a force-displacement graph
Power Output of a Rotating Object
Power is the rate of doing work, and is defined by
Where:
P = power (W)
ω = angular velocity (rad s–1)
This equation is the angular version of the linear equation P = Fv
Examiner Tips and Tricks
Don't forget that θ is always in radians when you're doing conversions from revs s–1 or rev min–1.
Frictional Torque
In rotational mechanics, frictional forces produce a specific torque called frictional torque
This is the torque caused by the frictional force when two objects in contact move past each other
Frictional torque can be defined as:
The difference between the applied torque and the resulting net, or observed, torque
This means that the net torque is the difference between the applied and frictional torque
Net torque = applied torque – frictional torque
In rotating machinery, power has to be expended to overcome frictional torque
This is due to resistive forces within the machinery
In most cases, frictional torque is minimised to reduce the kinetic energy losses transferred to heat and sound
The frictional force must always be subtracted from the torque resulting from an applied force to get the total or net torque in the system
Frictional torque is calculated using the same equations as torque
The only difference is F is the frictional force instead of an externally applied force
Worked Example
The figure below shows a type of circular saw. The blade is driven by an electric motor and rotates at 3100 rev min–1 when cutting a piece of wood.
A constant frictional torque of 2.7 N m acts at the bearings of the motor and axle.
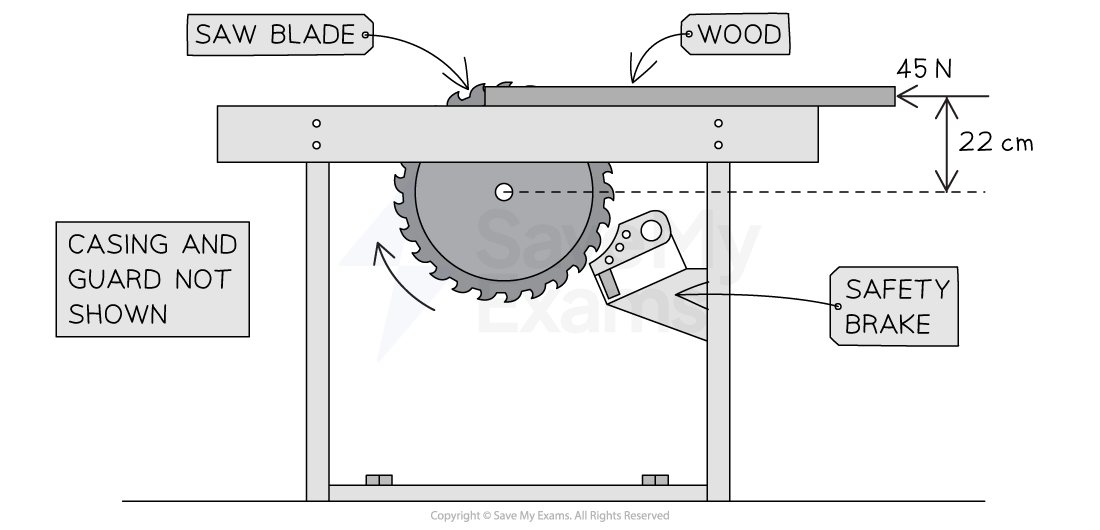
A horizontal force of 45 N is needed to push a piece of wood into the saw. The force acts on the blade at an effective radius of 22 cm.
Calculate the output power of the motor when the saw is cutting the wood.
Answer:
Step 1: Calculate the torque on the saw blade
When the wood is being cut, the torque from the 45 N force is equal to the net torque of the saw blade
Step 2: Calculate the applied torque on the saw from the motor
net torque = applied torque on the saw blade – frictional torque
Step 3: Calculate the angular velocity
1 revolution = 2π radians
3100 rev min–1 = 3100 × 2π rad min–1
min–1 → sec–1 = ÷ 60
Step 4: Calculate the output power

Unlock more, it's free!
Did this page help you?