Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsRotational DynamicsAngular Momentum

Angular Momentum (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Angular Momentum

  • Angular momentum is the rotational equivalent of linear momentum, which is defined by mass × velocity, or

space p space equals space m v

  • Therefore, angular momentum L is defined by

L space equals space I omega

  • Where:

    • L = angular momentum (kg m2 rad s−1)

    • I = moment of inertia (kg m2)

    • omega = angular velocity (rad s−1)

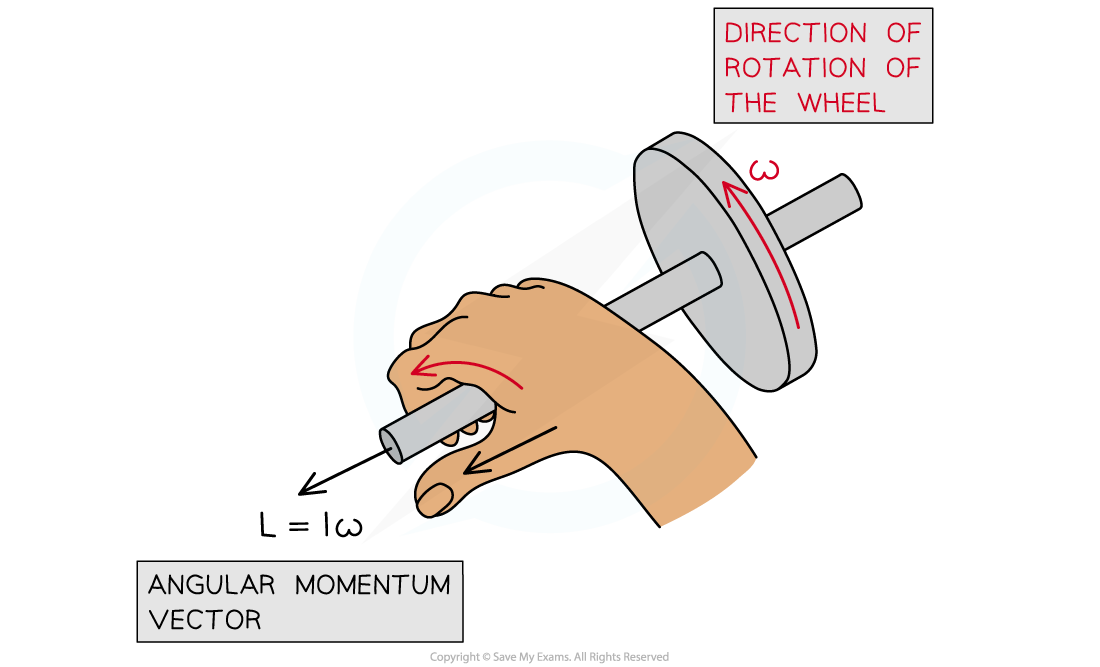
12-1-7-quantization-ib-hl

The angular momentum of a rotating wheel is the product of the moment of inertia and angular velocity of the wheel

Angular Momentum of a Point Mass

  • The moment of inertia of a rotating point mass m which is a distance r from an axis of rotation is equal to

I space equals space m r squared

  • The angular velocity of the point mass is given by

omega space equals space v over r

  • Therefore, the angular momentum of the point mass is equal to

L space equals space I omega space equals space open parentheses m r squared close parentheses cross times v over r space equals space m v r

Worked Example

A horizontal rigid bar is pivoted at its centre so that it is free to rotate. A point particle of mass 3M is attached at one end of the bar and a container is attached at the other end, both are at a distance of R from the central pivot. 

A point particle of mass M moves with velocity v at right angles towards the stationary rod as shown in the diagram.

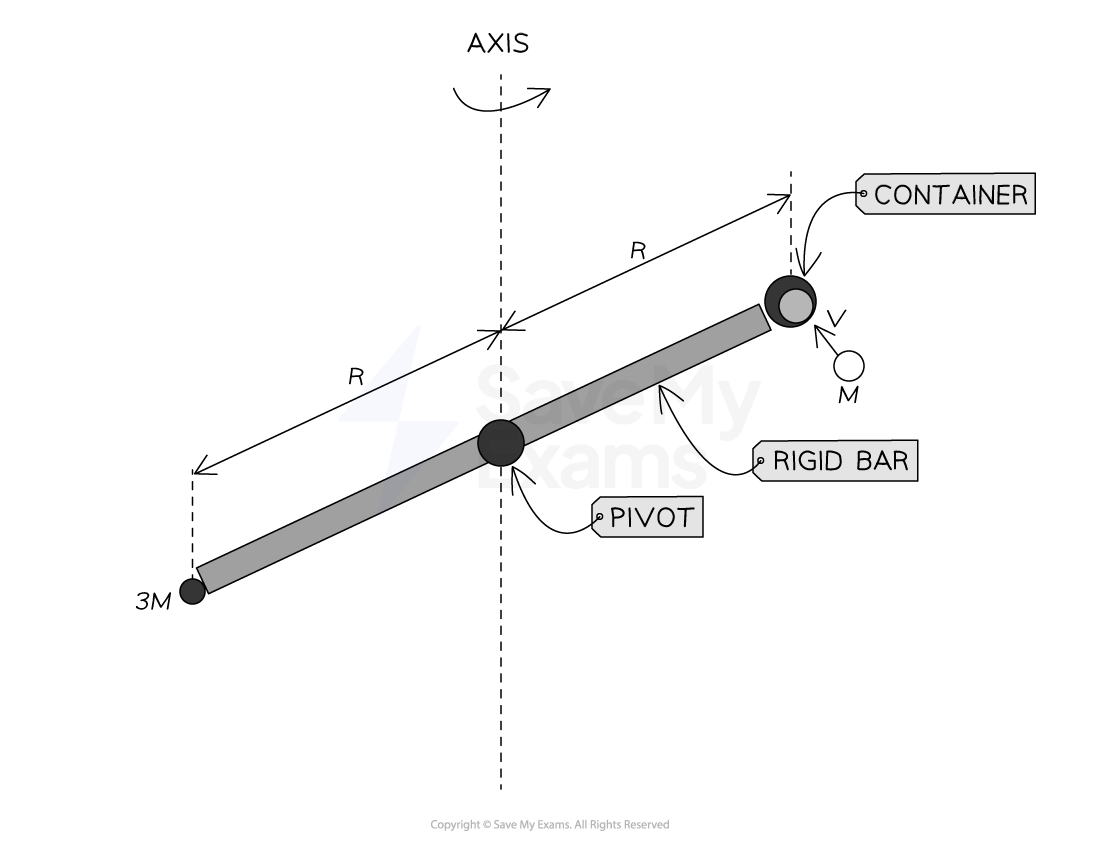
11-1-6-rigid-bar-angular-momentum-worked-example

The particle M collides with the container which is at a distance of R just before the collision from the centre of the point of rotation of the bar and stays within it as the system starts to rotate about the vertical axis with angular velocity ω.

The mass of the rod and the container are negligible.

Write an expression for the angular momentum of the system about the vertical axis just after the collision, in terms of M, R and ω.

Answer:

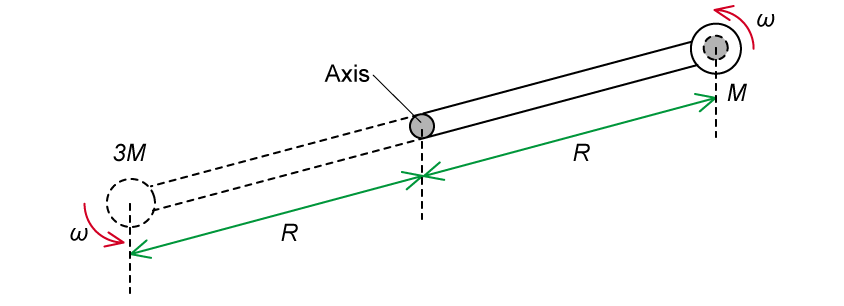
1-4-7-angular-momentum-of-a-system-worked-example-ma2-ib-2025-physics

  • The whole system rotates with an angular velocity of ω

  • The rod and the container as massless, so we only need to consider the angular momentum of the two masses M and 3M

  • Therefore, the angular momentum of the system after the collision is:

L space equals space capital sigma open parentheses I omega close parentheses

L space equals space open parentheses M R squared close parentheses omega space plus space open parentheses 3 M R squared close parentheses omega

L space equals space 4 M R squared omega

Examiner Tips and Tricks

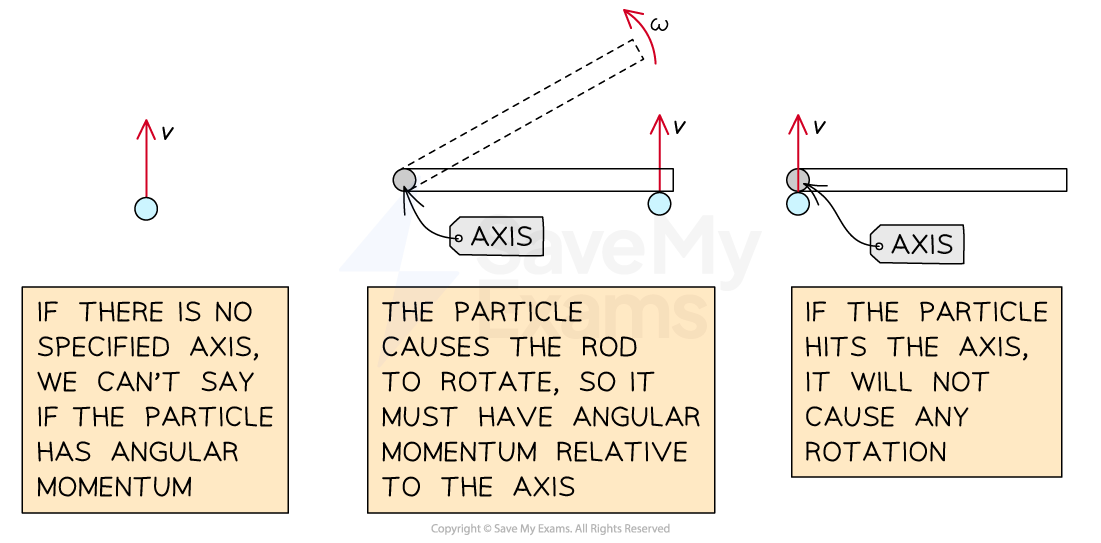
You should know that objects travelling in straight lines can have angular momentum - just make sure you understand that it all depends on the position of the object in relation to the axis of rotation being considered

1-4-7-angular-momentum-particle-in-a-straight-line-ib-2025-physics

Conservation of Angular Momentum

  • As with linear momentum, angular momentum is always conserved 

  • The principle of conservation of angular momentum states:

    The angular momentum of a system always remains constant, unless a net torque is acting on the system

  • This conservation law has many real-world applications, for example

    • A person on a spinning chair spins faster while their arms and legs are contracted and slower while extended

    • Objects in elliptical orbits travel faster nearer the object they orbit and slower when further away

    • Ice skaters can change their rotational velocity by extending or contracting their arms

    • Tornados spin faster as their radius decreases

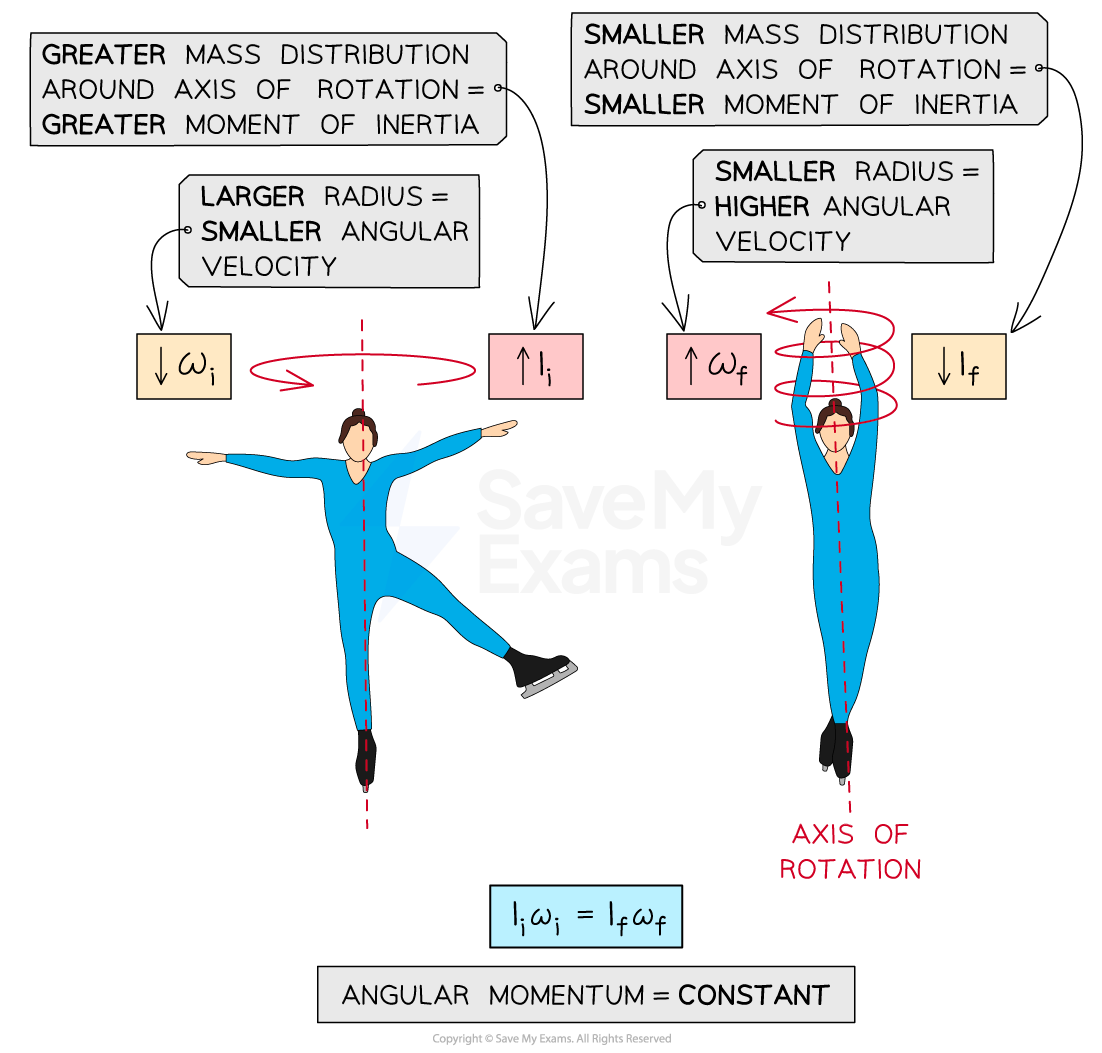
1-4-7-conservation-of-angular-momentum-ice-skater

Ice skaters can change their moment of inertia by extending or contracting their arms and legs. Due to the conservation of angular momentum, this allows them to spin faster or slower

  • Problems involving a change in angular momentum can be solved using the equation:

I subscript i omega subscript i space equals space I subscript f omega subscript f

  • Where:

    • I subscript i = initial moment of inertia (kg m2)

    • omega subscript i = initial angular velocity (rad s−1)

    • I subscript f = final moment of inertia (kg m2)

    • omega subscript f = final angular velocity (rad s−1)

Worked Example

The diagram shows the different positions of a diver between jumping off a springboard and entering the water.

During their fall, the diver pulls their arms and legs into a tight tuck position while in the air and straightens them before entering the water.

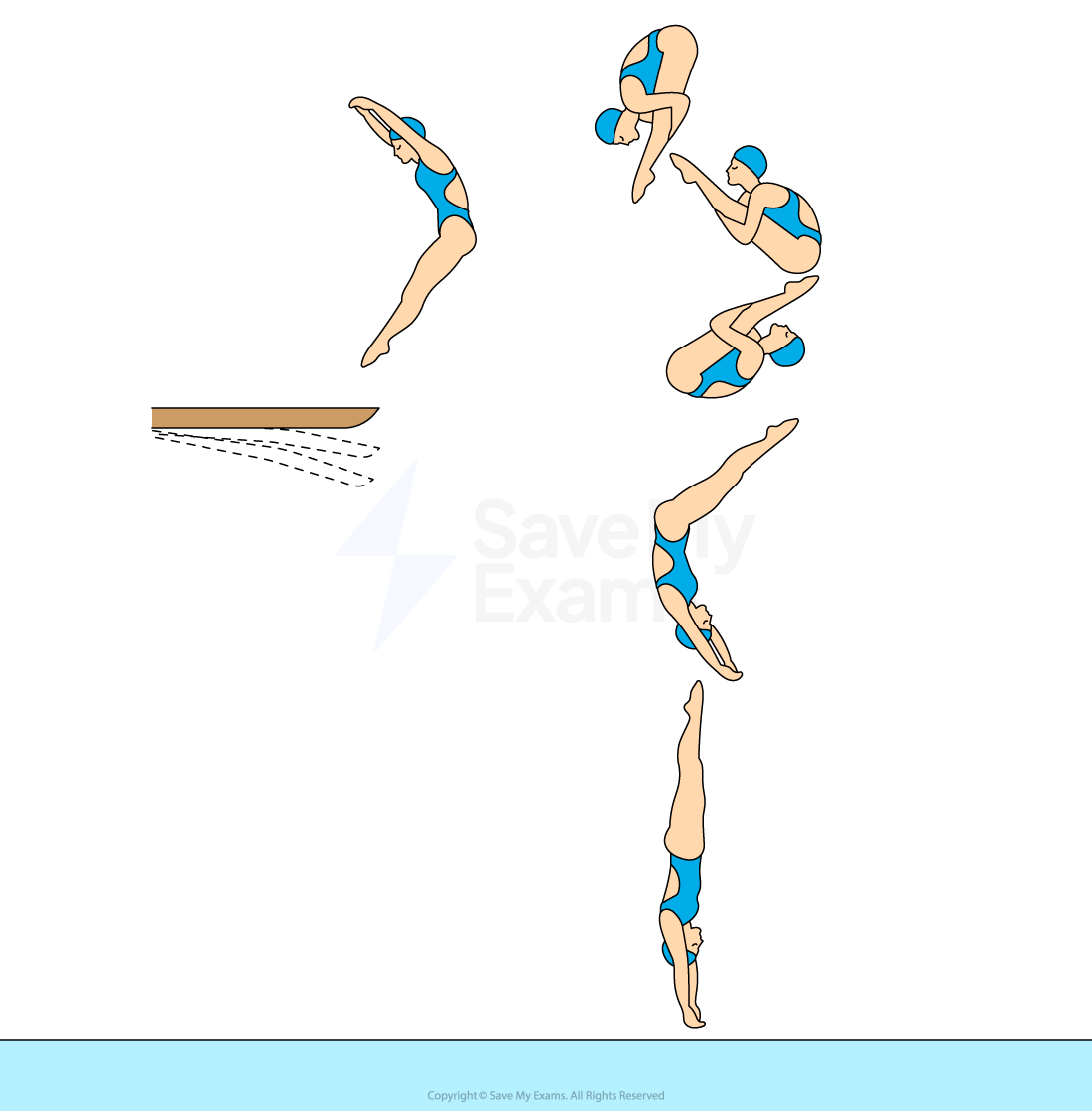
8YT3mwKp_1-4-7-conservation-of-angular-momentum-diver-mcq-worked-example

Which row correctly describes the changes to the diver's moment of inertia and angular velocity as they bring their limbs closer to their body?

 

moment of inertia

angular velocity

A.

increases

increases

B.

decreases

increases

C.

increases

decreases

D.

decreases

decreases

Answer: B

  • After the diver leaves the springboard, there is no longer a resultant torque acting on them

    • This means their angular momentum remains constant throughout the dive

  • Due to the conservation of angular momentum:

I subscript i omega subscript i space equals space I subscript f omega subscript f space equals space c o n s t a n t

  • When the diver tucks their arms and legs in closer to their body, they decrease their moment of inertia

    • This eliminates options A & C

  • Therefore, to conserve angular momentum, when the diver's moment of inertia decreases, their angular velocity must increase

Worked Example

A spherical star of mass M and radius R rotates about its axis. The star explodes, ejecting mass in space radially and symmetrically. The remaining star is left with a mass of 1 over 10 M and a radius of 1 over 50 R.

Calculate the ratio of the star’s final angular velocity to its initial angular velocity.

The moment of inertia of a sphere is 2 over 5 M R squared

Answer:

  • Before the star explodes:

    • Initial moment of inertia, I subscript i space equals space 2 over 5 M R squared

    • Initial angular velocity = omega subscript i

  • After the star explodes:

    • Final moment of inertia, I subscript f space equals space 2 over 5 open parentheses 1 over 10 M close parentheses open parentheses 1 over 50 R close parentheses squared

    • Final angular velocity = omega subscript f

  • From the conservation of angular momentum:

I subscript i omega subscript i space equals space I subscript f omega subscript f

open parentheses 2 over 5 M R squared close parentheses omega subscript i space equals space open parentheses 2 over 5 cross times 1 over 10 M cross times open parentheses 1 over 50 close parentheses squared R squared close parentheses omega subscript f

open parentheses up diagonal strike 2 over 5 M R squared end strike close parentheses space omega subscript i space equals space open parentheses up diagonal strike 2 over 5 M R squared end strike close parentheses space fraction numerator 1 over denominator 25 space 000 end fraction omega subscript f

  • Therefore, the ratio of the star’s final angular velocity to its initial angular velocity is:

omega subscript f over omega subscript i space equals space 25 space 000

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Newton’s Second Law for RotationNext:Angular Impulse
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.