A LevelPhysicsAQARevision NotesEngineering PhysicsRotational DynamicsNewton’s Second Law for Rotation

Newton’s Second Law for Rotation (AQA A Level Physics) : Revision Note

Ashika

Author

Ashika

Last updated

Newton’s Second Law for Rotation

  • In linear motion, the force required to give an object a certain acceleration depends on its mass

F space equals space m a

  • This is Newton's Second Law of linear motion, where:

    • F = force (N)

    • m = mass (kg)

    • a = linear acceleration (m s−2)

  • In rotational motion, the torque required to give a rotating object a certain angular acceleration depends on its moment of inertia

tau space equals space I alpha

  • This is Newton's Second Law of rotational motion, where:

    • tau = torque (N m)

    • I = moment of inertia (kg m2)

    • alpha = angular acceleration (rad s−2)

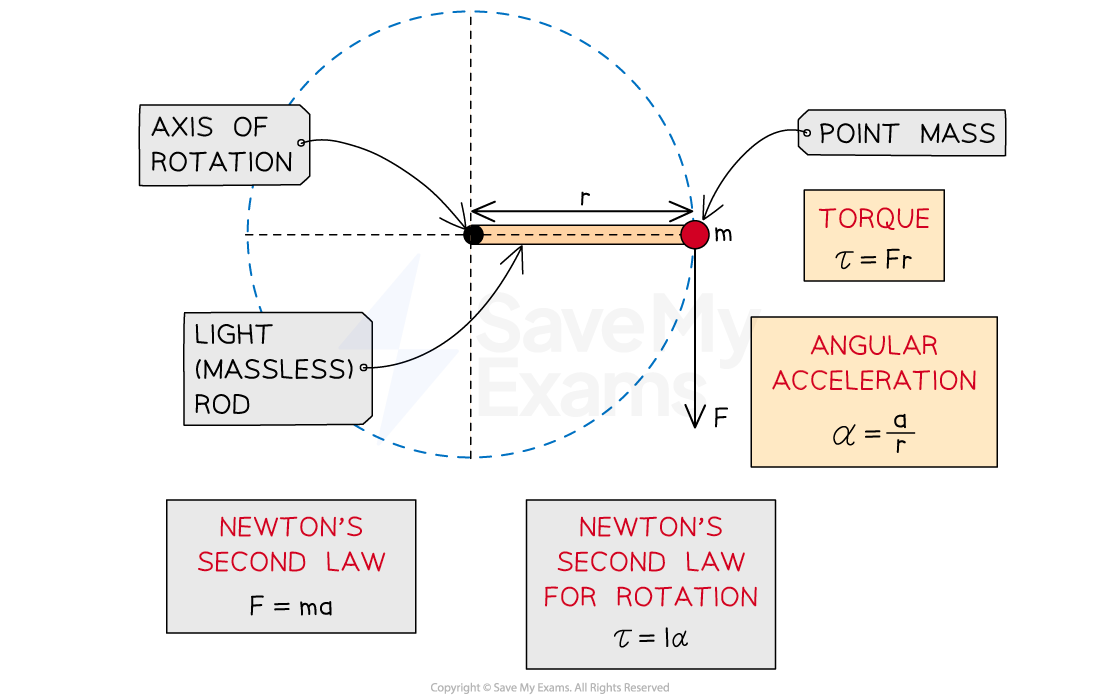
rZNng5oC_1-4-6-newtons-second-law-for-rotation

Newton's second law for rotating bodies is equivalent to Newton's second law for linear motion

  • This equation comes from the fact that torque is the rotational equivalent of force:

Force:  F space equals space m a

Torque:  tau space equals space F r

  • Where:

    • r = perpendicular distance from the axis of rotation (m)

  • Combining these equations gives:

tau space equals space r open parentheses m a close parentheses

  • The moment of inertia of a rotating body can be thought of as analogous to (the same as) mass

    • The inertia of a mass describes its ability to resist changes to linear motion, which is referring to linear acceleration

    • Similarly, the moment of inertia of a mass describes its ability to resist changes to rotational motion, which is referring to angular acceleration

Angular acceleration:  alpha space equals space a over r

Moment of inertia (point mass):  I space equals space m r squared

  • Using these equations with the equations for force and torque leads to:

tau space equals space r open parentheses m r alpha close parentheses

tau space equals space open parentheses m r squared close parentheses alpha

tau space equals space I alpha

Comparison of linear and rotational variables in Newton's Second Law

Linear variable

Rotational variable

Force, F

Torque, tau

Mass, m

Moment of inertia, I

Acceleration, a

Angular acceleration, alpha

Newton's Second Law, F space proportional to space a

Newton's Second Law, tau space proportional to space alpha

F space equals space m a

tau space equals space I alpha

Worked Example

A block of mass m is attached to a string that is wrapped around a cylindrical pulley of mass M and radius R, as shown in the diagram.

The moment of inertia of the cylindrical pulley about its axis is 1 half M R squared.

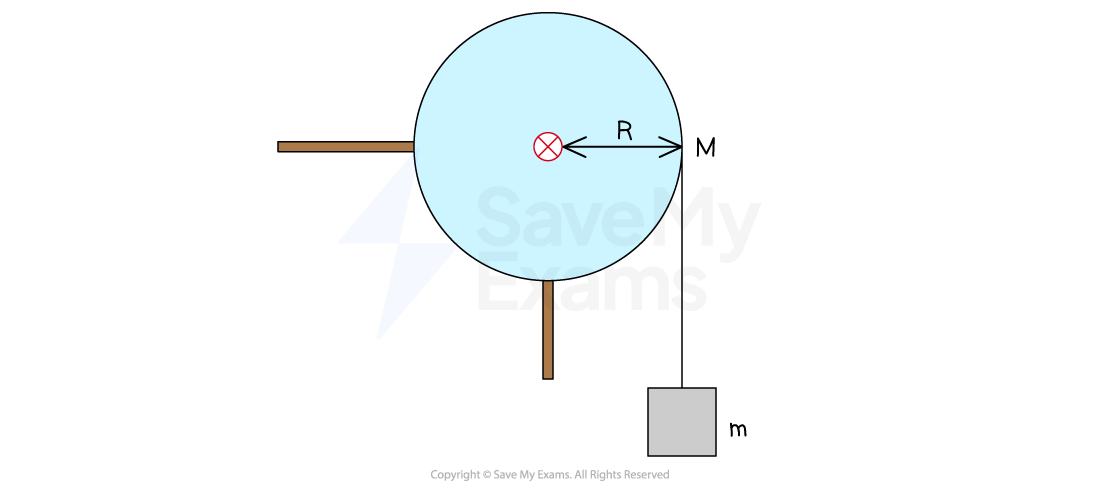
YAsQNsP5_1-4-6-newtons-second-law-for-rotation-worked-example

When the block is released, the pulley begins to turn as the block falls.

Write an expression for the acceleration of the block.

Answer:

Step 1: Identify the forces acting on the block

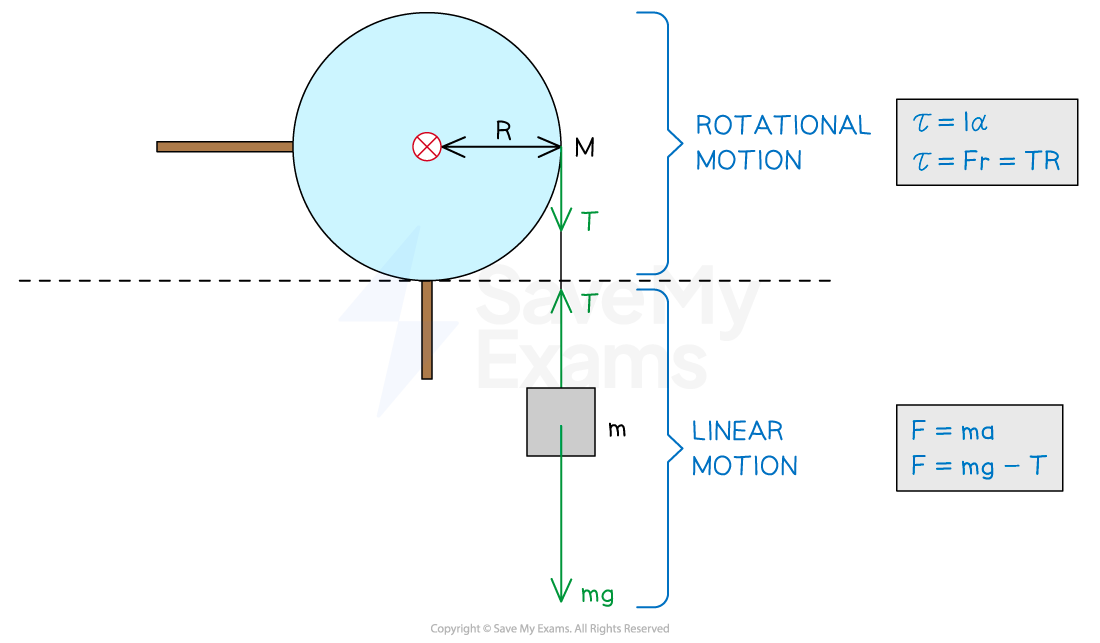
Q2Dp7PX~_1-4-6-newtons-second-law-for-rotation-worked-example-ma

Step 2: Apply Newton's second law to the motion of the block

F space equals space m a

m g space minus space T space equals space m a  eq. (1)

Step 3: Apply Newton's second law to the rotation of the pulley

tau space equals space I alpha

T R space equals space I alpha

Step 4: Write the equation for the pulley in terms of acceleration a

  • The angular acceleration alpha of the pulley is: 

alpha space equals space a over R

  • Substitute this into the previous equation:

T R space equals space I a over R

  • Substitute in the expression for the moment of inertia and simplify:

Moment of inertia of the cylinder:  I space equals space 1 half M R squared

T R space equals space open parentheses 1 half M R squared close parentheses a over R

T space equals space open parentheses 1 half M R squared close parentheses a over R squared space equals space 1 half M a  

T space equals space 1 half M a  eq. (2)

Step 5: Substitute eq. (2) into eq. (1) and rearrange for acceleration a

m g space minus space 1 half M a space equals space m a

m g space equals space m a space plus space 1 half M a space equals space a open parentheses m space plus space M over 2 close parentheses

Acceleration of the block:  a space equals space fraction numerator m g over denominator m space plus space M over 2 end fraction

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Moment of InertiaNext:Angular Momentum
Ashika

Author: Ashika

Expertise: Physics Content Creator

Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.

Download notes on Newton’s Second Law for Rotation