Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsRotational DynamicsMoment of Inertia

Moment of Inertia (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Moment of Inertia

  • In linear motion, the resistance to a change of motion, i.e. linear acceleration, is known as inertia

    • The larger the mass an object has, the greater its inertia

  • In rotational motion, the distribution of mass around an axis must be considered, using moments of inertia

    • This is the rotational equivalent of mass

  • The moment of inertia of a rigid, extended body is defined as:

    The resistance to a change of rotational motion, depending on the distribution of mass around a chosen axis of rotation

  • Moment of inertia is measured in kg m2

  • The moment of inertia of a body corresponds to how 'easy' or 'hard' it is to rotate, and this is dependent on many factors, including

    • The total mass (m)

    • How its mass is distributed about the axis of rotation (r)

      • For example, if a springboard diver jumps off a board and does a flip, they tuck their legs closer to their chest. This decreases their moment of inertia, as more of their mass is distributed over a smaller distance. This makes it easier for them to rotate

The change in the moment of inertia of a diver

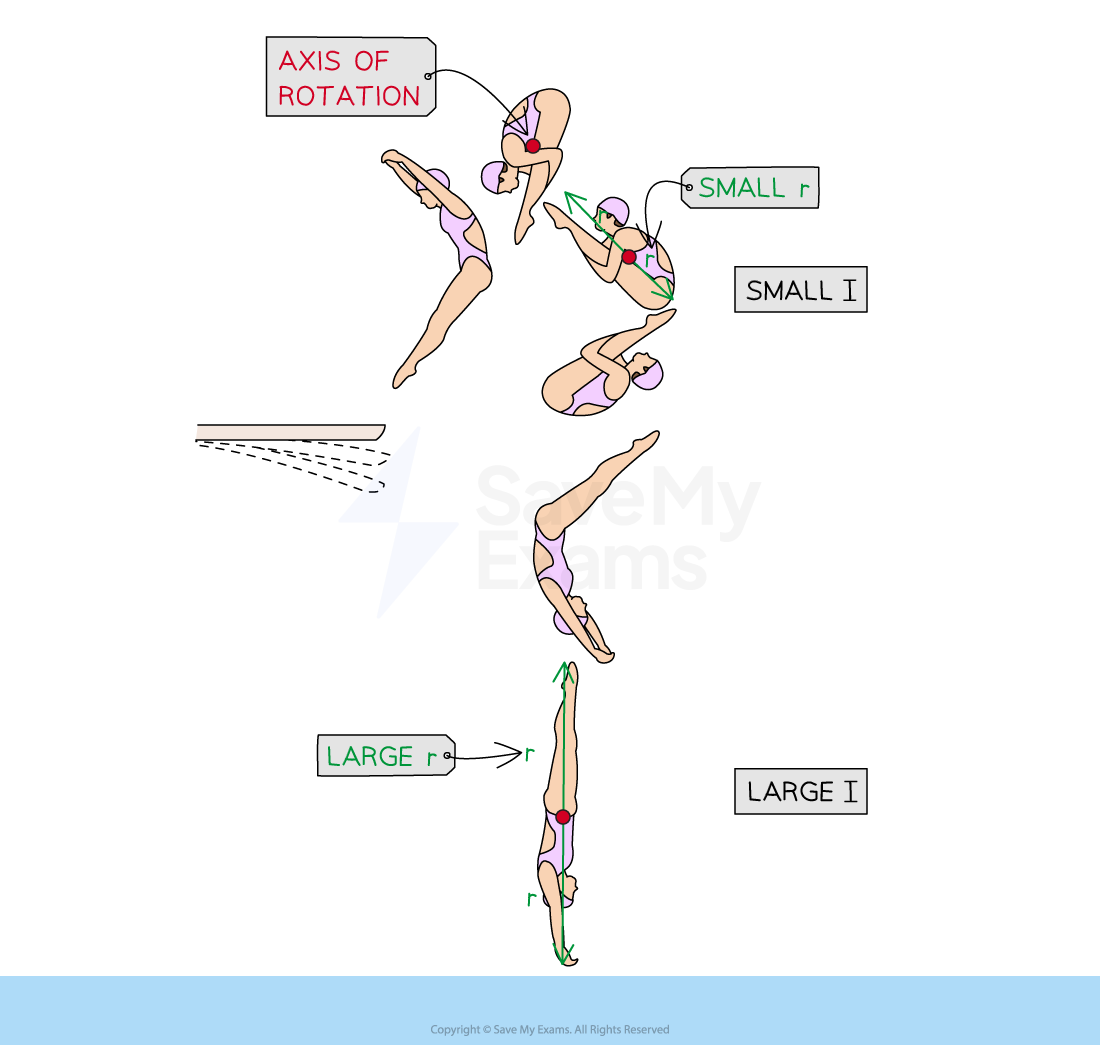
11-1-4-moment-of-inertia-rotation-diver

The distance from the axis of rotation changes as the diver curls up and straightens out again

  • This also means that the moment of inertia of a singular object can change depending on its orientation in relation to the chosen axis of rotation

  • For example, the moment of inertia of a thin rod is different for each of the following orientations:

    • Rotation about its vertical axis

    • Rotation about its centre of mass

    • Rotation about one end

Different orientations of a thin rod have different moments of inertia

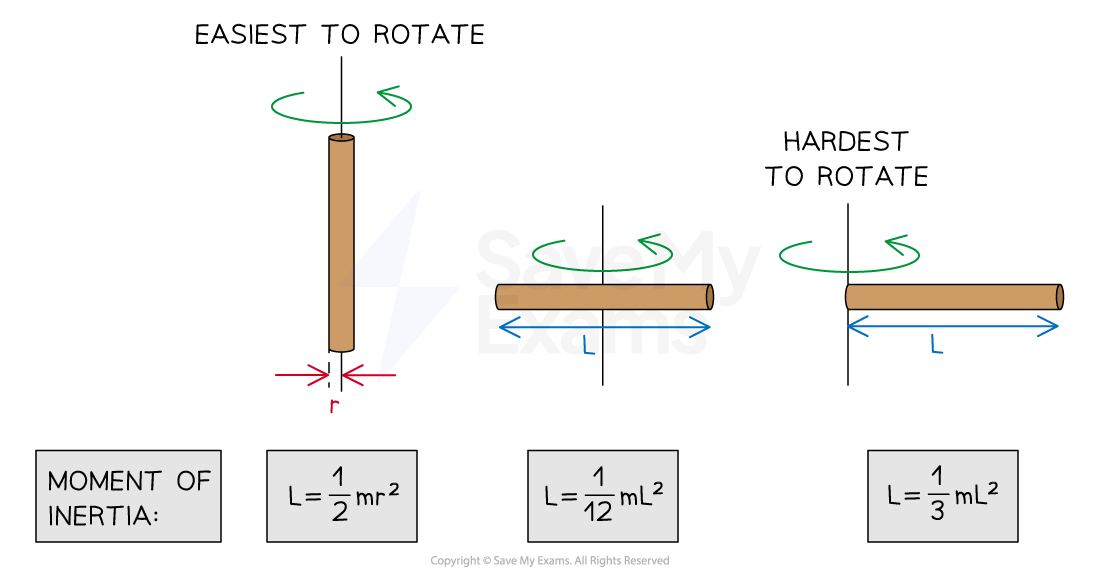
11-1-4-moment-of-inertia-rotation

The moment of inertia of a body can change depending on its orientation relative to the axis of rotation 

  • These are just a few of the possible orientations of the axis of rotation for a thin rod

    • There is an infinite range of possible axes, and therefore an infinite possible set of values for the moments of inertia

    • This also applies to nearly all rigid, extended objects that could be considered

Calculating Moments of Inertia

  • The moment of inertia I of a point mass is equal to

I space equals space m r squared

  • Where:

    • I = moment of inertia (kg m2)

    • m = mass of the object (kg)

    • r = distance from its axis of rotation (m)

  • The moment of inertia for an extended object about an axis is defined as the summation of the mass × radius2 for all the particles that make up the body

I space equals space sum m r squared

  • This gives the total moment of inertia of the system

Worked Example

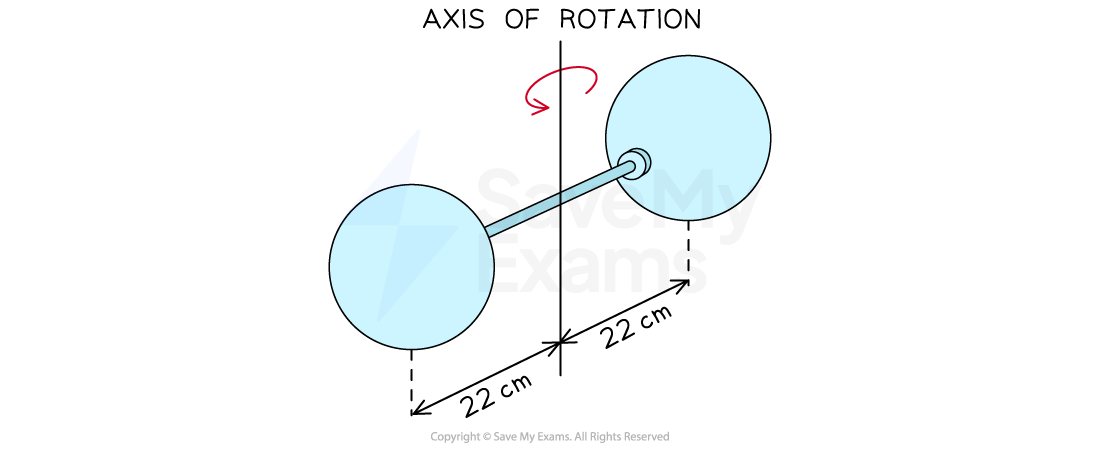
Two solid spheres form a dumbbell when attached to each end of a thin rod. The dumbbell rotates with the centre of mass of each sphere at a distance of 22 cm from the axis of rotation, as shown in the diagram.

The thin rod has a mass of 20 g. Each sphere has a radius of 4 cm and a mass of 750 g.

1-4-5-moments-of-inertia-dumbbell-arrangement-ib-2025-physics

Moment of inertia of a thin rod about its centre = 1 over 12 m L squared

Moment of inertia of a solid sphere = 2 over 5 m r squared

Determine

(a) the overall moment of inertia of the dumbbell arrangement

(b) the ratio of the moment of inertia of the thin rod to the overall moment of inertia of the dumbbell arrangement

 Answer:

Part (a)

  • The overall moment of inertia of the dumbbell is the sum of all the moments of inertia in the arrangement

I space equals space sum m r squared space equals space 2 cross times open parentheses 2 over 5 m subscript s p h e r e end subscript r squared close parentheses space plus space 1 over 12 m subscript r o d end subscript L squared

  • Where:

    • Mass of a sphere, m subscript s p h e r e end subscript = 750 g = 0.75 kg

    • Distance from axis to each sphere, r = 22 cm = 0.22 m

    • Mass of the rod, m subscript r o d end subscript = 20 g = 0.02 kg

    • Length of the rod, L = 2 × (22 − 4) = 36 cm = 0.36 m

I space equals space 2 cross times open parentheses 2 over 5 cross times 0.75 cross times 0.22 squared close parentheses space plus space open parentheses 1 over 12 cross times 0.02 cross times 0.36 squared close parentheses

Moment of inertia of the dumbbell:  I = 0.029 kg m2

Part (b)

  • The moment of inertia of the thin rod is 

I subscript r o d end subscript space space equals space 1 over 12 cross times 0.02 cross times 0.36 squared space equals space 2.16 space cross times space 10 to the power of negative 4 end exponent space kg space straight m squared

  • Therefore, the ratio I subscript r o d end subscript space divided by space I is

I subscript r o d end subscript over I space equals space fraction numerator 2.16 space cross times space 10 to the power of negative 4 end exponent over denominator 0.029 end fraction space equals space 0.0071

  • This means the rod contributes about 0.7% of the overall moment of inertia of the dumbbell

Examiner Tips and Tricks

You will never be expected to memorise the moments of inertia of different shapes, they will always be given in an exam question where required

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:TorqueNext:Newton’s Second Law for Rotation
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.