Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesEngineering PhysicsRotational DynamicsTorque

Torque (AQA A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Torque

  • The change in rotational motion due to a turning force is called torque

  • The torque of a force F about an axis is given by

tau space equals space F r

  • Where:

    • tau = torque (N m)

    • F = applied force (N)

    • r = perpendicular distance between the axis of rotation and the line of action of the force (m)

Torque of a perpendicular force

11-1-3-torque

The torque applied by a cyclist on a bicycle pedal can be determined using the magnitude of the applied force, from the cyclist, and the distance between the line of action of the force and the axis of rotation, the length of the crank arm r

Torque of a Couple

  • When applied to a couple (2 forces), torque can be described as:

    The sum of the moments produced by each of the forces in the couple

Torque of a couple on a steering wheel

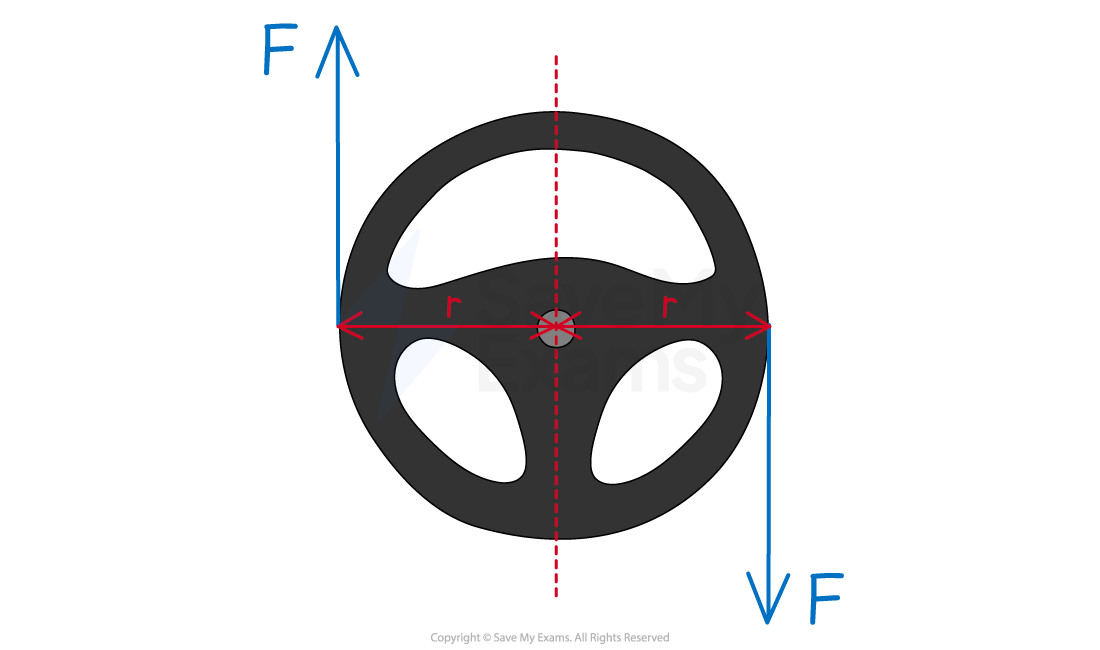
Torque of a Couple Steering Wheel Example, for IB HL Physics Revision Notes

The steering wheel is in rotational equilibrium since the resultant force and resultant torque are zero. This means it does not have linear or angular acceleration.

  • For example, the torque provided by a couple on a steering wheel of radius r is

tau space equals space open parentheses F space cross times space r close parentheses space plus thin space open parentheses F space cross times space r close parentheses space equals space 2 F r

  • Therefore, the torque of a couple is equal to double the magnitude of the torque of the individual forces

  • The forces are equal and act in opposite directions

    • Therefore, couples produce a resultant force of zero

  • Due to Newton’s Second law (F = ma), the steering wheel does not accelerate

    • In other words, when the force is applied, the steering wheel rotates with a constant angular speed but remains in the same location

Worked Example

A grinding wheel is used to sharpen the edges of pieces of wood in a school workshop. A piece of wood is forced against the edge of the wheel so that the tangential force on the wheel is a steady 12.0 N as the wheel rotates. The diameter of the wheel is 0.13 m.

Calculate the torque on the grinding wheel, giving an appropriate unit

Answer:

Step 1: State the equation for torque

tau space equals space F r

Step 2: Calculate the perpendicular distance from the axis of rotation

  •  This is the radius of the wheel since the rotation is from the centre of the wheel

r space equals fraction numerator space 0.13 over denominator 2 end fraction space equals space 0.065 space straight m

Step 3: Substitute the values

tau space equals space 12.0 space cross times space 0.065 space equals space 0.78

Step 4: State the appropriate unit

tau space equals space 0.78 space straight N space straight m

Examiner Tips and Tricks

The terminology in this section can get confusing.  For example, a moment is not a 'turning force' - the turning force is only part of the moment, the moment is the effect that the turning force has on the system when applied at a distance from a turning point, or pivot.

This is often linked with content from the moments section of the course.

Ultimately, when you carry out calculations, make sure you can identify

  • The magnitude of the applied force

  • The perpendicular distance between the force and the turning point (along the line of action)

When considering an object in rotational equilibrium, choosing certain points can simplify calculations of resultant torque. Remember you can choose any point, not just the axis of rotation.

To simplify your calculation, choose a point where the torque of (most of) the forces are unknown, or when you need to determine where the resultant torque is zero. To do this, choose a point through which the lines of action of the forces pass.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Angular Acceleration EquationsNext:Moment of Inertia
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.