The PET Scanner (AQA A Level Physics)

Positron Emission Tomography

• Positron Emission Tomography (PET) is defined as:

  A type of nuclear medical procedure that images tissues and organs by measuring the metabolic activity of the cells of body tissues

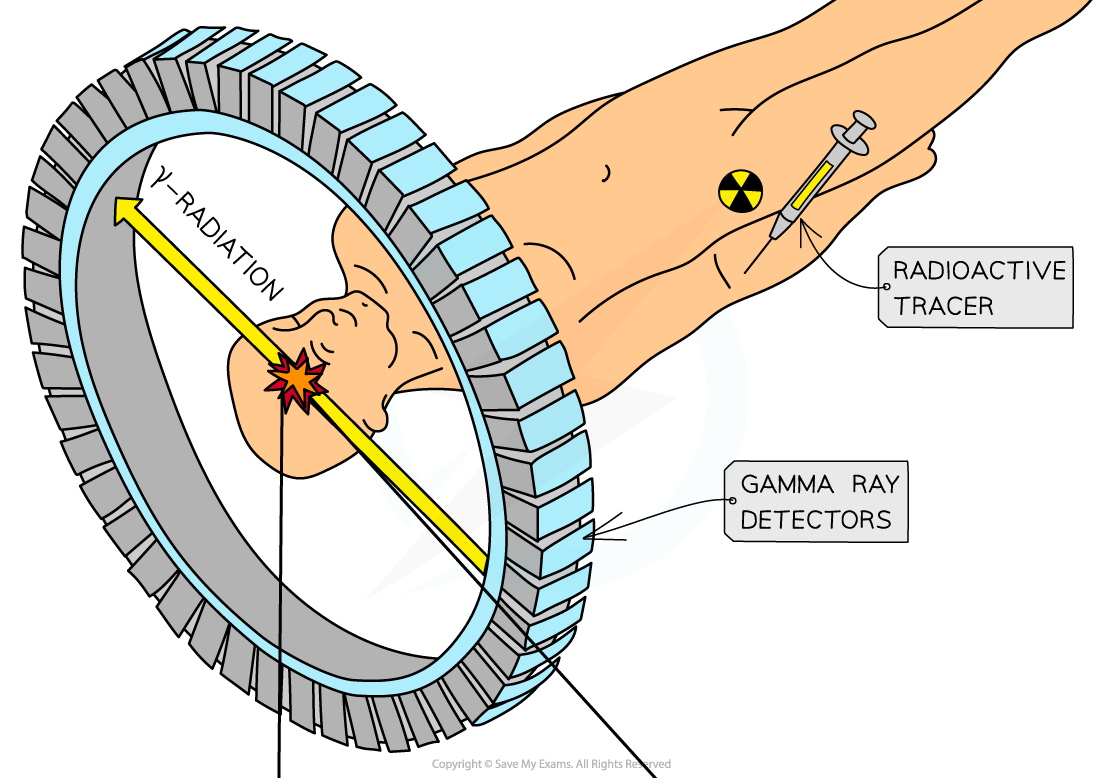
• In PET scanning, a beta-plus emitting radioactive tracer is used in order to stimulate positron-electron annihilation to produce gamma photons

  • These are then detected using a ring of gamma cameras

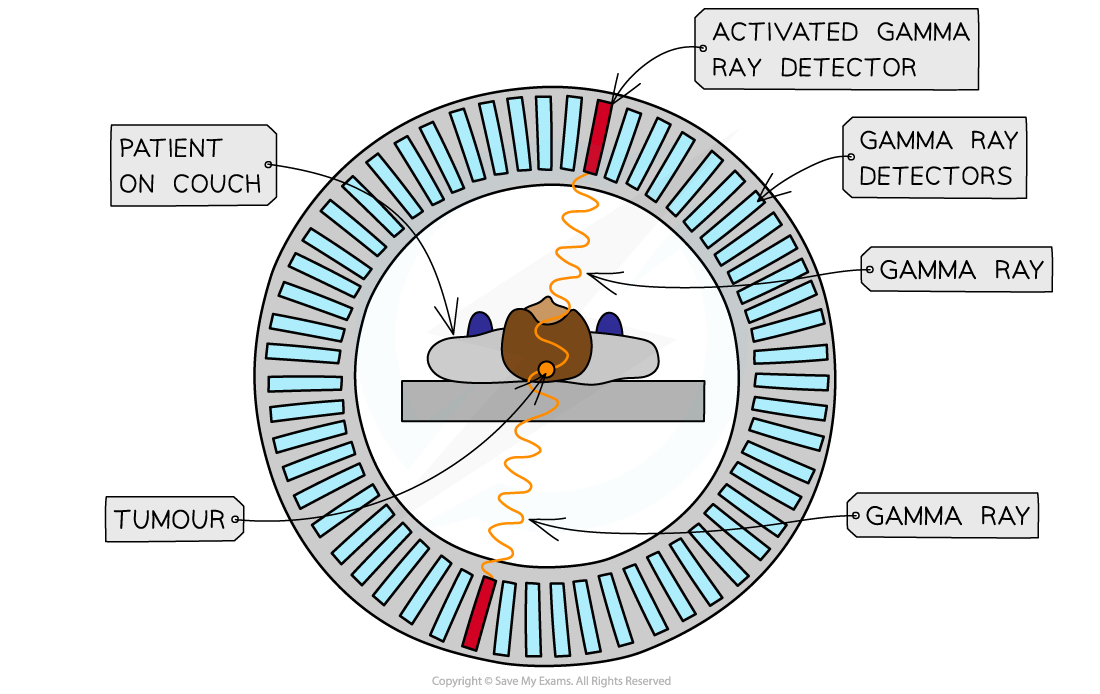
Principles of PET Scanning

Before the scan

• The patient is injected with a beta-plus emitting isotope, usually fluorine-18 (F-18)

During the scan

• The part of the body being studied is surrounded by a ring of gamma cameras

• The positrons from the F-18 nuclei annihilate with electrons in the patient

• The annihilation of a positron and an electron produces two identical gamma photons travelling in opposite directions

• The delay time between these two gamma-ray photons is used to determine the location of the annihilation due to the F-18 tracer

• Photons that do not arrive within a nanosecond of each other are ignored since they cannot have come from the same point

After the scan

• The signals from the gamma camera detectors are sent to a computer which builds up an image

A PET Scanner

Detecting gamma rays with a PET scanner

Annihilation

• Annihilation can happen between any particle and antimatter counterpart, but in PET scanning, only the electron and positron interaction is considered

• When a positron is emitted from a tracer in the body, it travels less than a millimetre before annihilating with an atomic electron

• As with all collisions, mass, energy and momentum are always conserved

An Electron-Positron Annihilation

Annihilation of a positron and electron to form two gamma-ray photons

• The gamma-ray photons produced each have an energy of 512 keV

  • This is the same each time as determined by the mass-energy equivalence of the positron-electron pair

• The energy of each photon is given by

• Where:

  • = mass of the electron or positron (kg)

  • = Planck's constant (J s)

  • = frequency of the photon (Hz)

  • = the speed of light in a vacuum (m s^–1)

Diagnosis Using PET Scanning

• The signals produced by the photomultiplier tubes are used to produce an image

• The γ rays travel in straight lines in opposite directions when formed from the annihilation of the positron and electron

  • This happens in order to conserve momentum

• They hit the detectors in a line – known as the line of response

• The tracers will emit lots of γ rays simultaneously, and the computers will use this information to create an image

• The more photons from a particular point, the more tracer that is present in the tissue being studied, and this will appear as a bright point on the image

• An image of the tracer concentration in the tissue can be created by processing the arrival times of the gamma-ray photons

Annihilation in the PET Scanner

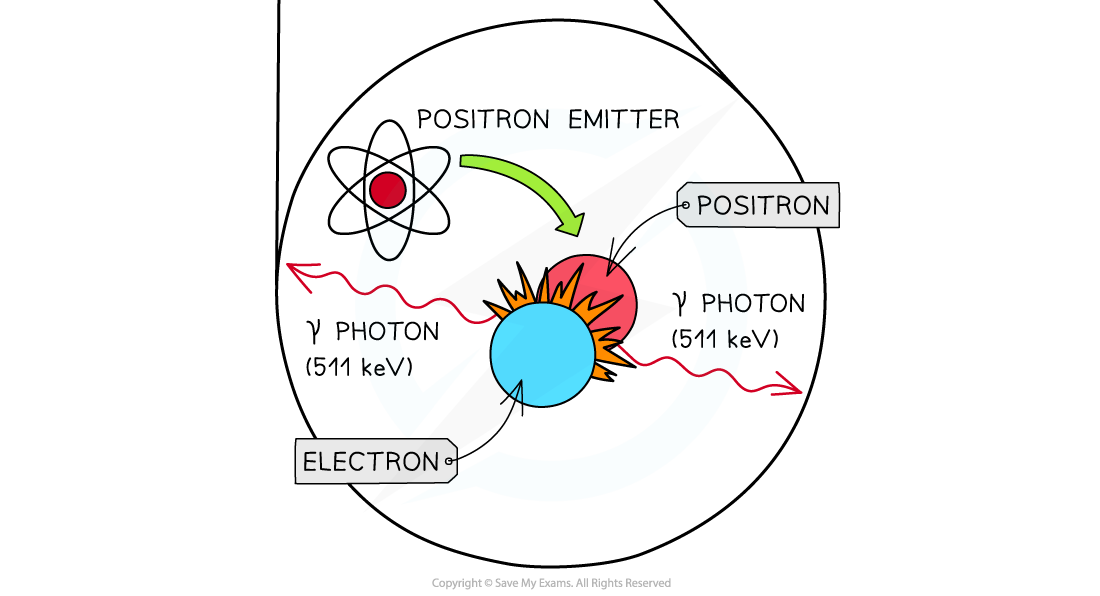
Annihilation of a positron and an electron is the basis of PET Scanning

• Once the tracer is introduced to the body it has a short half-life, so, it begins emitting positrons  immediately

  • This allows for a short exposure time to the radiation

  • A short half-life does mean the patient needs to be scanned quickly and not all hospitals have access to expensive PET scanners