Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesMedical PhysicsX-ray ImagingAttenuation of X-rays

Attenuation of X-rays (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Attenuation of X-rays in Matter

  • When a collimated beam of X-rays passes through a patient’s body, the X-ray photons are absorbed and scattered

  • Different materials absorb X-rays by different amounts

    • For example, bones absorb a large proportion of X-ray photons which is why they appear bright white on an X-ray image

  • As the X-rays pass through a material, the intensity of the beam is found to decay exponentially

    • This decrease in intensity is known as attenuation

  • The attenuation of X-rays can be calculated using the equation:

I space equals space I subscript 0 space e to the power of negative mu x end exponent

  • Where:

    • I subscript 0 = the intensity of the incident beam (W m-2)

    • I = the intensity of the transmitted beam (W m-2)

    • mu = the linear absorption coefficient (m-1)

    • x = distance travelled through the material (m)

  • The linear attenuation coefficient mu is defined as

    The fraction of X-rays removed per unit thickness of the material for a specified energy of the X-rays

  • The value of μ depends on the density of a substance and the energy of the X-ray photons 

    • The greater the density of a material, the greater the value of μ 

    • For example, bone absorbs a greater proportion of X-rays than soft tissue due to its higher density 

Absorption of X-rays by flesh and bone

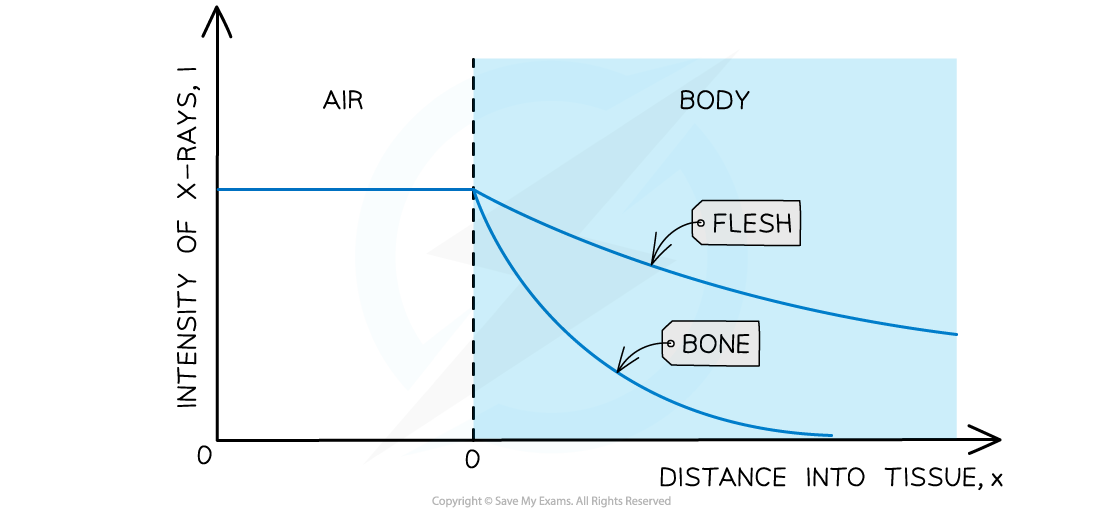
Attenuation of X-rays, downloadable AS & A Level Physics revision notes

Bone is denser than soft tissues, such as flesh, so X-rays are absorbed more over a shorter distance

Half-value thickness

  • Similar to half-life in radioactivity, a material's ability to absorb X-rays is known as its half-value thickness

  • The half-value thickness of a material can be defined as:

    The thickness of the material which will reduce the intensity of X-rays to half its original level for a specified energy of the X-rays

  • If the half-value thickness is x space equals space x subscript bevelled 1 half end subscript, then intensity has a value of I space equals space I subscript 0 over 2, so substituting this into the attenuation equation gives:

I subscript 0 over 2 space equals space I subscript 0 space e to the power of negative mu x subscript bevelled 1 half end subscript end exponent

1 half space equals space e to the power of negative mu x subscript bevelled 1 half end subscript end exponent

  • Taking natural logarithms of both sides gives

ln space 1 half space equals space minus mu x subscript begin inline style bevelled 1 half end style end subscript

ln space 2 space equals space mu x subscript begin inline style bevelled 1 half end style end subscript

  • Hence, the half-value thickness of a substance is given by:

x subscript bevelled 1 half end subscript space equals space fraction numerator ln space 2 over denominator mu end fraction

Worked Example

A student investigates the absorption of X-ray radiation in a model arm. A cross-section of the model arm is shown in the diagram.

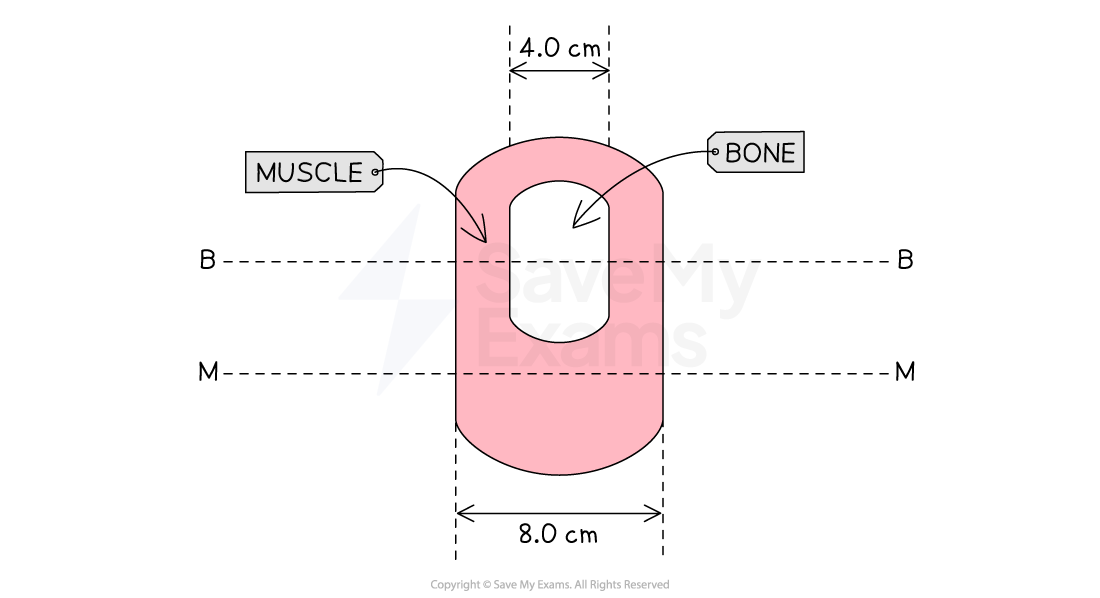
10-5-5-we-attenuation-of-x-rays-in-matter

Parallel X-ray beams are directed along line MM and line BB. The linear absorption coefficients of the muscle and the bone are 0.20 cm−1 and 12 cm−1 respectively.

Calculate the ratio:

fraction numerator i n t e n s i t y space o f space i n c i d e n t space X minus r a y space b e a m space f r o m space m o d e l over denominator i n t e n s i t y space o f space i n c i d e n t space X minus r a y space b e a m space o n space m o d e l end fraction

for a parallel X-ray beam directed along

(a) line MM

(b) line BB

and state whether the X-ray images have good contrast.

Answer:

Part (a)

Step 1: Write out the known quantities

  • Linear absorption coefficient for muscle, mu subscript m = 0.20 cm-1

  • Distance travelled through the muscle, x subscript m = 8.0 cm

Step 2: Write out the equation for attenuation and rearrange

I space equals space I subscript 0 space e to the power of negative mu x end exponent

  • Where I = the intensity of the incident X-ray beam from the model

  • And I subscript 0 = the intensity of the incident X-ray beam on the model

fraction numerator i n t e n s i t y space o f space i n c i d e n t space X minus r a y space b e a m space f r o m space m o d e l over denominator i n t e n s i t y space o f space i n c i d e n t space X minus r a y space b e a m space o n space m o d e l end fraction equals I over I subscript 0 equals e to the power of negative mu x end exponent

Step 3: Substitute in values and calculate the ratio

I over I subscript 0 space equals space e to the power of negative open parentheses 0.20 cross times 8.0 close parentheses end exponent space equals space 0.2

Part (b)

Step 1: Write out the known quantities

  • Linear absorption coefficient for muscle, mu subscript m = 0.20 cm-1

  • Linear absorption coefficient for bone, mu subscript b = 12 cm-1

  • Distance travelled through the muscle, x subscript m = 4.0 cm

  • Distance travelled through the bone, x subscript b = 4.0 cm

Step 2: Write out the equation for attenuation for two media and rearrange

I over I subscript 0 space equals space e to the power of negative mu subscript m x subscript m end exponent space cross times space e to the power of negative mu subscript b x subscript b end exponent

Step 3: Substitute in values and calculate the ratio

I over I subscript 0 space equals space e to the power of negative open parentheses 0.20 cross times 4.0 close parentheses end exponent space cross times space e to the power of negative open parentheses 12 cross times 4 close parentheses end exponent space equals space 6.4 cross times 10 to the power of negative 22 end exponent space almost equal to space 0

Step 4: Write a concluding statement

  • Each ratio gives a measure of the amount of transmission of the beam from the model

  • A good contrast is when:

    • There is a large difference between the intensities

    • The ratio is much less than 1.0

  • Therefore, both images have a good contrast

Differential Tissue Absorption

  • The amount of attenuation of a beam of X-rays depends on

    • The density of the absorbing tissue

    • The energy of the X-ray photons

  • The linear attenuation coefficient μ of an absorber is proportional to the density ρ of the absorbing substance

    • The higher the density of a material, the more X-ray energy that it absorbs

    • This is because the photons interact with more atoms, or a larger mass of atoms, in the same volume

  • Therefore, dividing the value of μ of a material by its density gives a constant value for that particular substance

  • This constant is known as the mass attenuation coefficient

mu subscript m space equals space mu over rho

  • Where:

    • mu subscript m = mass attenuation coefficient (m2 kg–1)

    • mu = linear attenuation coefficient (m–1)

    • rho = density of the absorbing material (kg m–3)

  • The mass attenuation coefficient of a substance describes how easily a beam of X-rays of a certain energy can penetrate it

    • The greater the mass attenuation coefficient, the stronger the absorption of X-rays by the material

    • The lower the mass attenuation coefficient, the greater the penetration of X-rays through the material

Mass attenuation coefficients for common elements

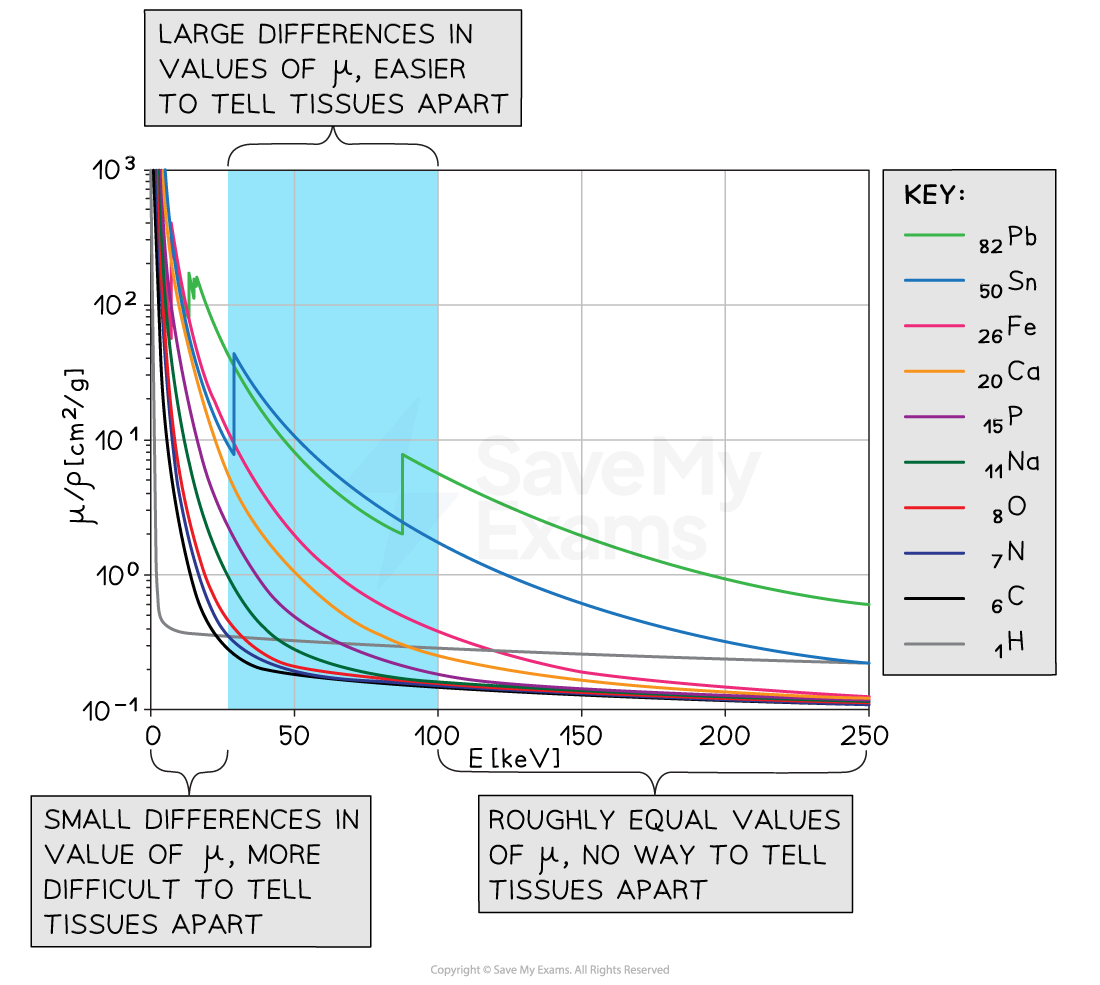
Khb1YscN_10-5-5-x-ray-mass-attenuation-different-elements

At very high and very low X-ray energies, differences in attenuation are very small. The optimum range for distinguishing different tissues is 30 keV to 100 keV

Photons of energies less than 30 keV...

  • Are absorbed by soft tissue and bone

  • Therefore, these photons are removed from the X-ray beam by placing a suitable metal filter (e.g. lead or tin) in the path of the X-ray beam

Photons of energies between 30 keV and 100 keV...

  • Are absorbed more readily by bone than by soft tissue

  • This is because the elements in bone have higher atomic numbers than the elements in soft tissues so bone can absorb photons in this energy range more readily

  • Therefore, these photons are used to distinguish between soft tissue and bone

Photons of energies greater than 100 keV...

  • Are absorbed more equally in all types of tissue, including bone

  • This means they produce no distinction between any tissues

  • Therefore, these photons are not used in diagnostic X-ray imaging

Attenuation in different elements

  • The graph of mass attenuation coefficient and X-ray photon energy for elements with different values of atomic number Z shows that 

    • Elements with lower Z values tend to absorb a lower proportion of X-rays

    • Elements with higher Z values tend to absorb a greater proportion of X-rays

  • The table below shows the composition of different substances and the effect of atomic number on attenuation

Substance

Elements

Effect on attenuation

soft tissue

hydrogen open parentheses straight H presubscript 1 presuperscript blank close parentheses, carbon open parentheses C presubscript 6 presuperscript blank close parentheses and oxygen open parentheses straight O presubscript 8 presuperscript blank close parentheses

lower Z values, less attenuation

bone

hydrogen open parentheses H presubscript 1 presuperscript blank close parentheses, carbon open parentheses C presubscript 6 presuperscript blank close parentheses, oxygen open parentheses straight O presubscript 8 presuperscript blank close parentheses, calcium open parentheses Ca presubscript 20 presuperscript blank close parentheses and phosphorus open parentheses straight P presubscript 15 presuperscript blank close parentheses

higher Z values, more attenuation

contrast media

 iodine open parentheses I presubscript 53 presuperscript blank close parentheses and barium open parentheses Ba presubscript 56 presuperscript blank close parentheses

very high Z values, very large attenuation

ideal for improving contrast

heavy metals

lead open parentheses Pb presubscript 82 presuperscript blank close parentheses and tin open parentheses Sn presubscript 50 presuperscript blank close parentheses

very high Z values, high attenuation at lower energies 

ideal for use as metal filters

 

Worked Example

A monochromatic beam of X-rays passes through an aluminium sheet of thickness 2.5 mm. The intensity of the beam is reduced by 25%.

Calculate the mass attenuation coefficient for these X-rays.

The density of aluminium is 2700 kg m−3

Answer:

Step 1: List the known quantities:

  • Intensity of X-ray beam, I space equals space open parentheses 1 minus 0.25 close parentheses I subscript 0 space equals space 0.75 space I subscript 0

  • Thickness of aluminium sheet, x = 2.5 mm = 0.0025 m

  • Density of aluminium, rho = 2700 kg m−3 

Step 2: Determine the linear attenuation coefficient of the X-rays

I space equals space I subscript 0 space e to the power of negative mu x end exponent

0.75 space I subscript 0 space equals space I subscript 0 space e to the power of negative 0.0025 mu end exponent

0.75 space equals space e to the power of negative 0.0025 mu end exponent

  • Take natural logs of both sides:

ln space 0.75 space equals space minus 0.0025 mu

mu space equals space minus fraction numerator space ln space 0.75 space over denominator 0.0025 end fraction

linear attenuation coefficient:  mu = 115 m−1

Step 3: Determine the mass attenuation coefficient of the X-rays

mu subscript m space equals space mu over rho

mu subscript m space equals space 115 over 2700

mass attenuation coefficient:  mu subscript m = 0.043 m2 kg−1

Worked Example

The table shows the linear attenuation coefficients for bone and muscle at three different X-ray photon energies.

Photon energy / keV

Bone μ / cm–1

Muscle μ / cm–1

30

2.13

0.41

50

0.68

0.24

80

0.36

0.20

100

0.30

0.18

 Determine the energy of X-ray photons that would produce an image of muscle next to bone with the best contrast.

Answer:

Step 1: Recall the factor that determines the quality of contrast

  • Contrast depends on the difference in attenuation

    • The smaller the difference in attenuation, the poorer the contrast

    • The larger the difference in attenuation, the better the contrast

Step 2: Determine the difference between the values of attenuation at each energy

  • At 30 keV, the difference in attenuation is 2.13 − 0.41 = 1.72 cm–1

  • At 50 keV, the difference in attenuation is 0.68 − 0.24 = 0.44 cm–1

  • At 80 keV, the difference in attenuation is 0.36 − 0.20 = 0.16 cm–1

  • At 100 keV, the difference in attenuation is 0.30 − 0.18 = 0.12 cm–1

  • The difference between µ of bone and muscle is greatest using 30 keV X-rays hence this energy would produce an image with the best contrast

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:X-ray DetectionNext:The CT Scanner
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.