Equal Loudness Curves (AQA A Level Physics): Revision Note
Exam code: 7408
Equal Loudness Curves
The normal human ear can detect sounds of frequencies from about 20 Hz to 20 000 Hz
Different people may perceive sound differently due to a range of factors
For example, hearing loss can occur due to ageing or exposure to excessive noise
Equal loudness curves can be produced to gain an understanding of an individual's hearing abilities
All sounds on a given curve are perceived as equally loud
An equal loudness curve is a plot of intensity level, in dB, against frequency, in Hz
Both axes use a logarithmic scale to match the large range of intensities and frequencies the human ear can detect
Equal Loudness Curve for a Normal Ear
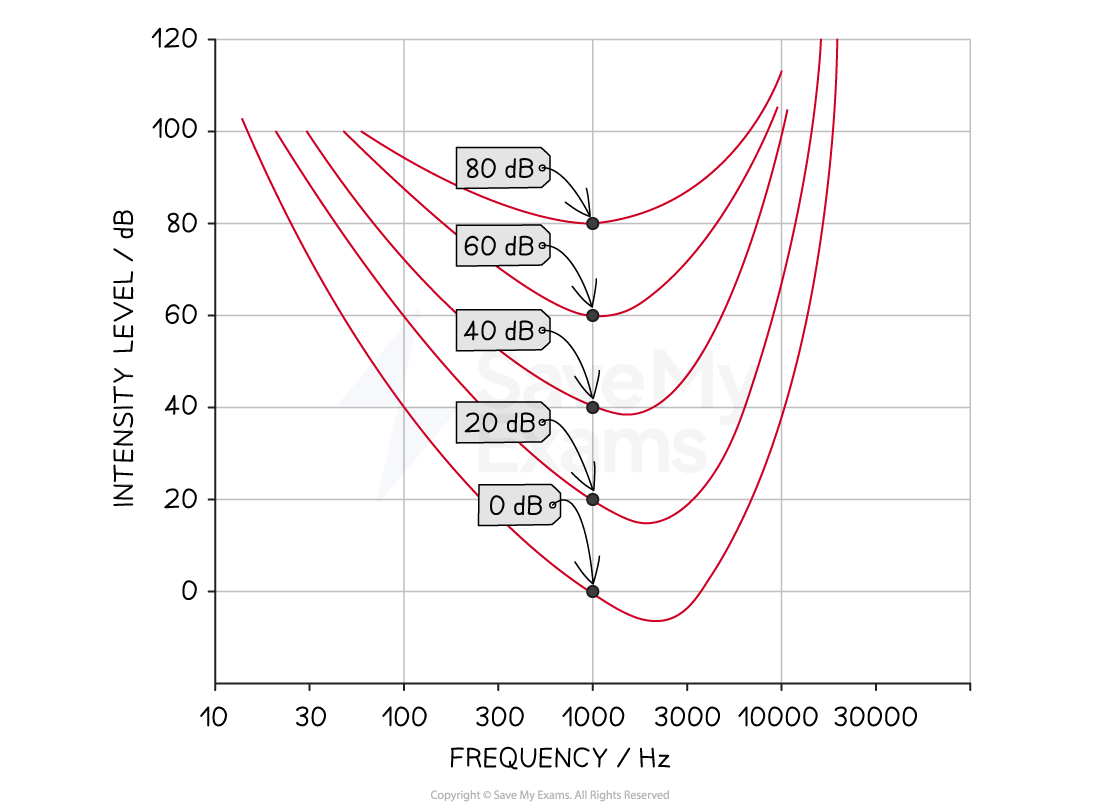
Equal loudness curves for a normal ear show the sound intensity level required to produce the same sensation of loudness at different frequencies
The loudness of a sound, for a given person, can be measured by comparing it with a standard source of sound at 1 kHz
The process for generating an equal loudness curve is as follows:
A reference signal is played through a pair of earphones - this is a sound of frequency 1 kHz at a fixed intensity level (volume)
A sound of a different frequency is played through the earphones
The intensity level (volume) of the sound is adjusted until both sounds seem to have the same loudness - the intensity level of this point is recorded
The process is repeated at different frequencies, then a curve can be plotted on a graph of intensity level against frequency - this is the equal loudness curve
Worked Example
On the axes below, sketch an equal loudness curve showing the normal response of a healthy ear.
Annotate the frequency axis with an appropriate scale.
Answer:
Step 1: Recall the frequency range of human hearing
For a normal ear, the range of human hearing is 20 to 20,000 Hz
Step 2: Recall how to plot a logarithmic scale
On a logarithmic scale, each large division on the scale represents an increase by the base of the log (usually 10) to a power that increases linearly (i.e. 101, 102, 103)
Then for each small division, instead of progressing linearly (e.g. 0, 1, 2, 3, 4...), a logarithmic scale progresses nonlinearly, but still in equal increments (e.g. 10, 20, 30, 40...)
Step 3: Label the frequency axis with a logarithmic scale
There are 3 large divisions on the axes provided, so we should plot the frequencies between 100, 1000 and 10 000 Hz, as this range is where the ear is most sensitive
10, 100 and 1000 Hz would be too low of a range
1000, 10 000 and 100 000 Hz would be too large of a range
Between the large divisions, there are 9 small divisions - there is no 'zero' on a logarithmic scale, so each small division represents increments of 100 and 1000 respectively

The scale should start at 100 Hz, then 1000 Hz at the midpoint, and end at 10 000 Hz
Between 100 Hz and 1000 Hz, each division on the scale represents 100 Hz
Between 1000 Hz and 10 000 Hz, each division on the scale represents 1000 Hz
Therefore, the locations of 300 Hz and 3000 Hz are two divisions from 100 Hz and 1000 Hz respectively
Step 4: Draw a U-shaped curve with the lowest point at 3000 Hz
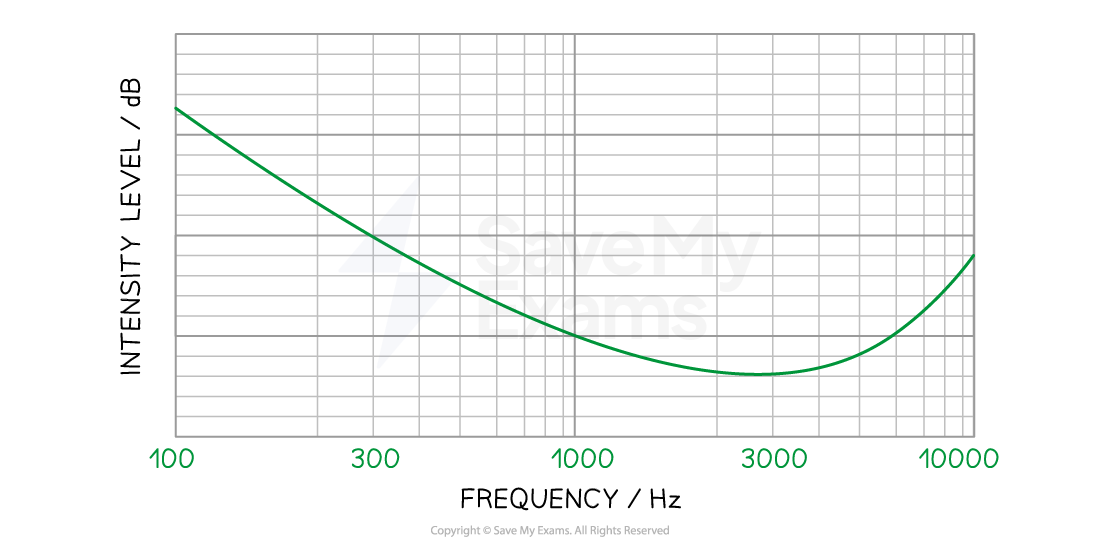
The equal loudness curve for a normal ear has a U-shape
The frequency a normal ear is most sensitive to is about 3000 Hz
Therefore, this corresponds to the quietest sound or lowest intensity level on the decibel scale
Worked Example
The diagram shows the equal loudness curve obtained when a patient has a hearing test at a level above the threshold of hearing.
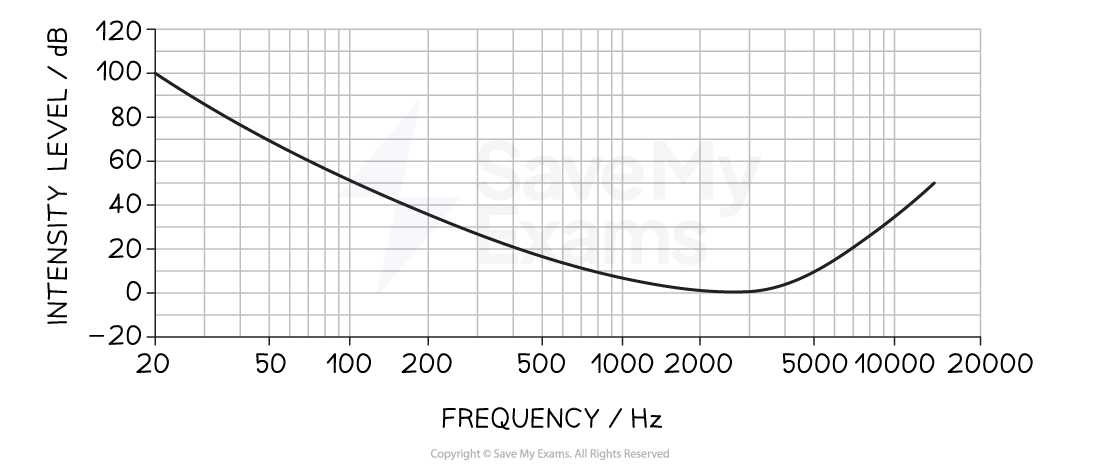
(a) Explain how the equal loudness curve was obtained.
(b) On the diagram draw an equal loudness curve which passes through 100 dB at a frequency of 1 kHz.
Answer:
Part (a)
Hearing test to generate the equal loudness curve:
The patient listens to a reference sound at 1 kHz and intensity level 10 dB
Then they listen to a sound at a different frequency and loudness
They switch between the sound at 1 kHz and the sound at the new frequency and the loudness is adjusted until the same loudness is perceived - the value of loudness is recorded
The process is repeated for frequencies between 20 Hz and 20 kHz
Part (b)
Equal loudness curve for 100 dB at 1000 Hz:
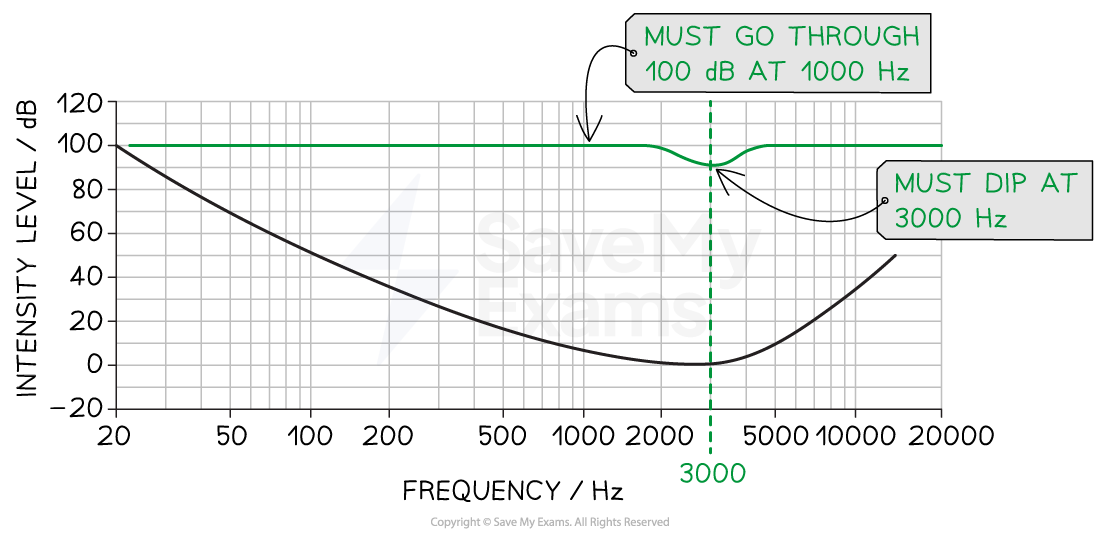
The general shape should be flatter and must pass through point 100 dB at 1000 Hz
Both curves are most sensitive at about 3000 Hz, so they both have a minimum intensity level here
Examiner Tips and Tricks
An understanding of the unit 'phon' is not required in this specification but you may come across it in your revision of equal loudness curves, so it is included here to aid your understanding
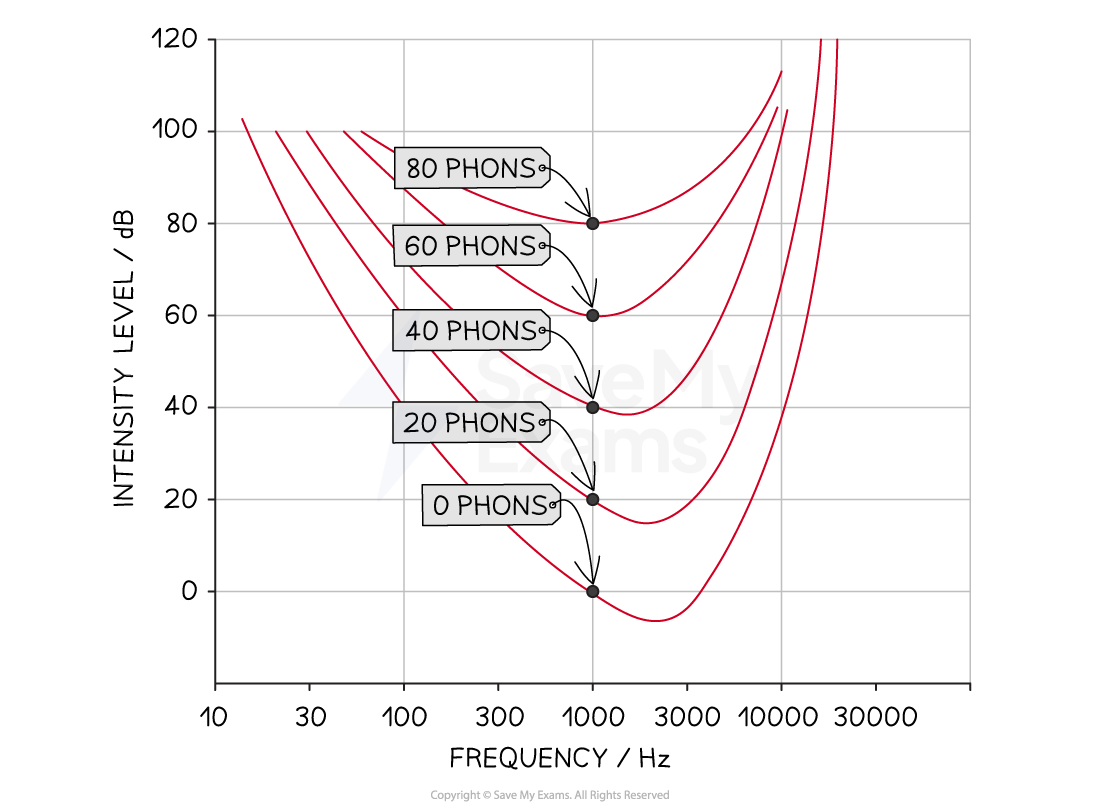
The loudness of a sound in phons is defined as the intensity level in decibels of a sound at 1000 Hz that has the same loudness as the sound, i.e. a 40 dB sound at 1000 Hz has a loudness of 40 phons. From the same curve, a 100 dB sound at 10 000 Hz also has a loudness of 40 phons.
Decibel Scales
Sound-level meters are usually calibrated on an adjusted decibel scale, or the dBA scale
The dBA scale gives relative measurements which take into account the ear's response to different frequencies
For example, the human ear is particularly sensitive to frequencies around 3 kHz and less sensitive to frequencies higher and lower than 3 kHz
This means that for the frequency response calibrated on the dBA scale:
Sounds of the same intensity level (in dB) have the same loudness on the dBA scale - the dB output is a flat line
At 1 kHz, the dB response and dBA response are set to be identical
At frequencies other than 1 kHz, the dBA response is a curve which reaches a maximum value around 3 kHz
The dBA Scale
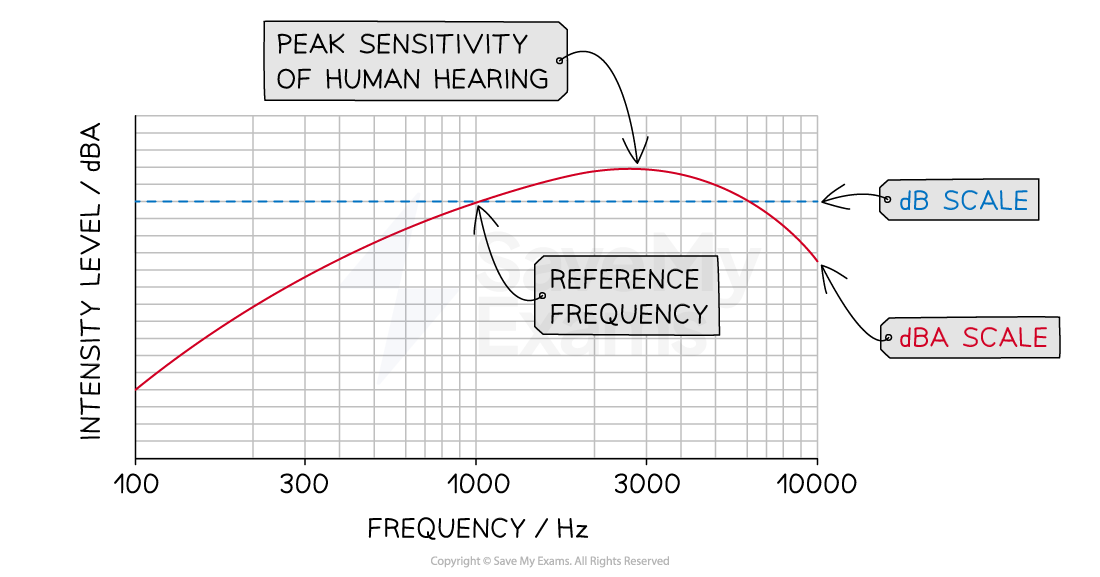
The red curve shows the dBA response which simulates the response of the ear at different frequencies. The blue dotted line shows the dB response which gives an equal response across all frequencies
At a frequency of 1 kHz (the reference frequency):
Both scales have the same intensity level
At frequencies above 1 kHz:
There is an increase up to a maximum of 3 kHz (the peak sensitivity of human hearing)
Then, there is a steady decrease to simulate the ear’s decreased sensitivity to higher frequencies
At frequencies below 1 kHz:
There is a steady decrease to simulate the ear’s decreased sensitivity to lower frequencies
Worked Example
A sound source of constant output power is used to generate a sound which is measured using a sound meter. When set to the dB scale, the sound meter displayed 80 dB as the reading when the frequency of the sound was 1 kHz.
State and explain:
(a) the main differences between the dB and dBA scales.
(b) what the reading would be for a sound of frequency 1 kHz if the meter was changed to the dBA scale.
(c) what would happen to the reading on each scale if the frequency of the sound was changed to 1.5 kHz.
Answer:
Part (a)
The dB scale is not frequency dependent, so the output is the same at all frequencies
The dBA scale is frequency dependent, so threshold intensities are different for different frequencies
Frequencies on the dBA scale are adjusted to match the response of the human ear
Part (b)
The reading on the dBA scale would be 80 dBA as 1 kHz is the reference frequency (at the threshold of hearing)
Part (c)
The dB reading would be 80 dB as the power is constant (and dB scale is not frequency dependent)
The dBA reading would be more than 80 dB as the ear is more sensitive at 1.5 kHz than at 1 kHz (or 1.5 kHz has a lower threshold intensity)
Examiner Tips and Tricks
Make sure you can draw the graph of intensity level in dBA against frequency - the key points to remember are
The dB line is flat
The dBA curve has the inverse shape to the equal loudness curve
The dBA curve peaks at 3 kHz (frequency of maximum sensitivity)
Both scales should have the same reading at 1 kHz (the reference frequency)

Unlock more, it's free!
Did this page help you?