Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesMedical PhysicsPhysics of the EarThe Decibel Scale

The Decibel Scale (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Relative Intensity Levels of Sound

  • When the sound waves enter the auditory canal, a stationary wave is set up

    • This can be modelled as a tube with an antinode forming at the open end and a node forming at the closed end

  • As a result, the auditory canal acts as a closed tube resonator which enhances the sensitivity of sounds in specific ranges

    • In the case of human hearing, this is what enables us to hear sounds in the range of 20 Hz to 20,000 Hz

    • The highest sensitivity region is around 2 to 5 kHz, which corresponds to frequencies of speech

Resonance in the Auditory Canal

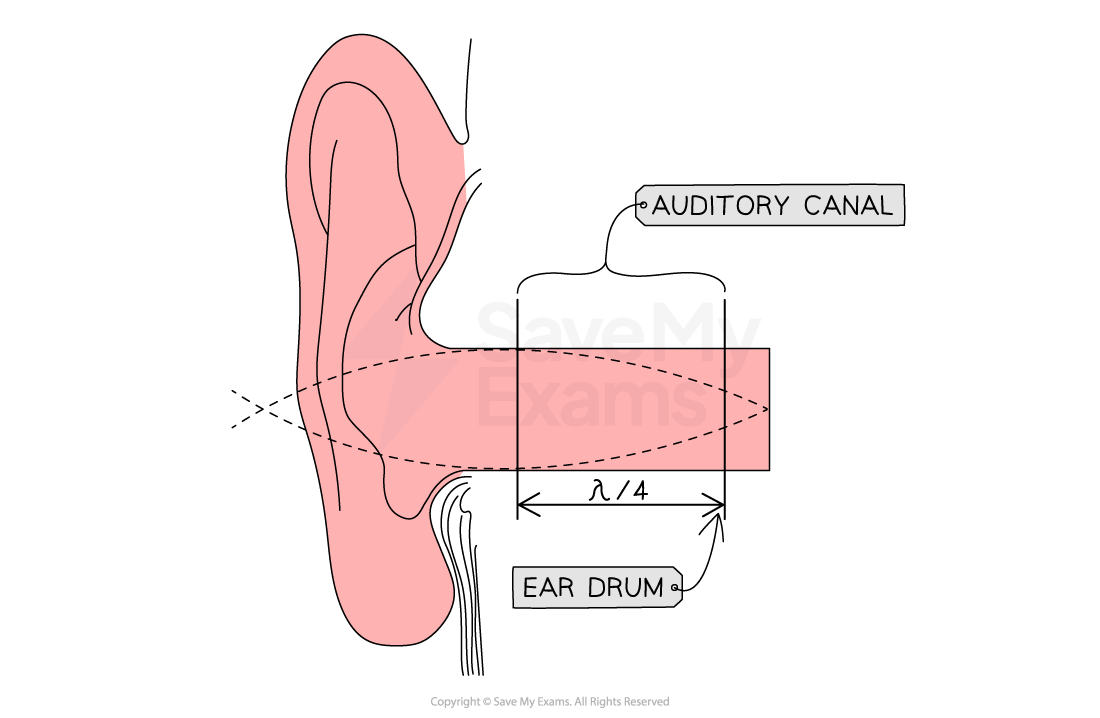
10-2-2-auditory-canal-resonance

The auditory canal works as a closed tube resonator which is sensitive to specific ranges of frequencies

The Decibel Scale

  • The ear’s ability to detect small changes in sound intensity is referred to as its sensitivity

    • This is measured in decibels (dB)

  • The sensitivity of human hearing depends on the frequency of the sound

  • The graph of sound intensity and frequency shows that the ear is most sensitive to sounds with a frequency of about 3000 Hz

The Relationship between Sound Intensity and Frequency 

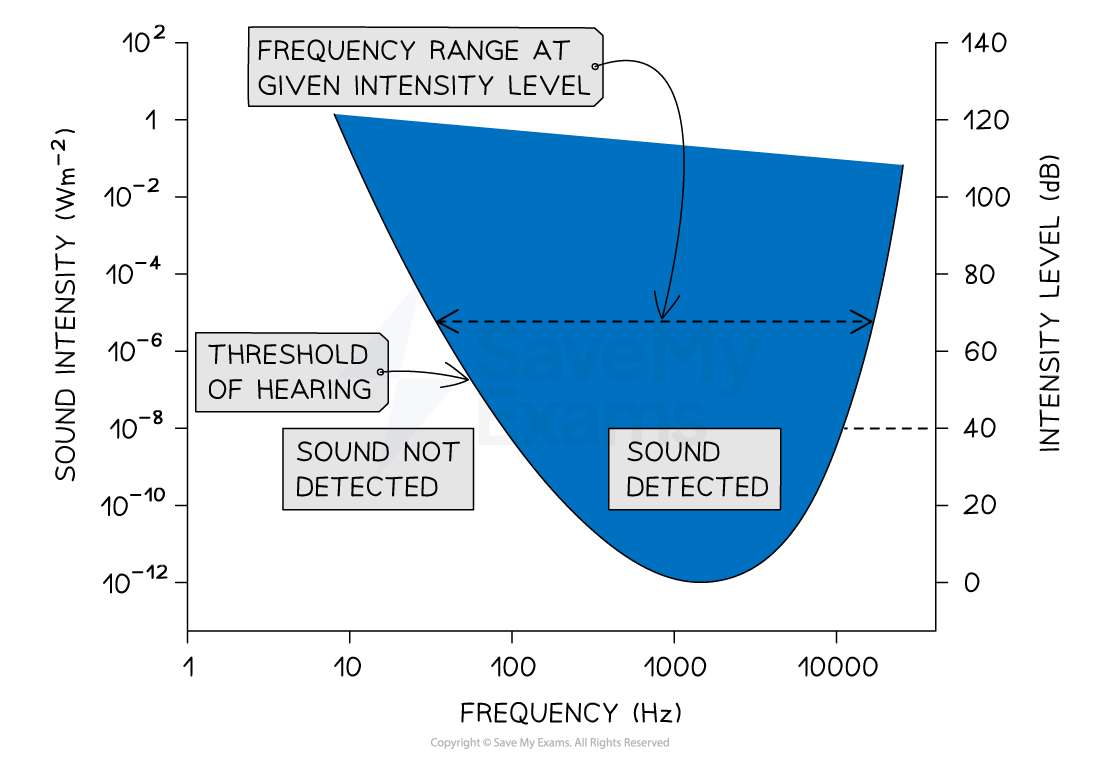
10-2-2-intensity-frequency-response-of-hearing

The human ear is most sensitive to sounds with a frequency of around 3000 Hz 

  • For frequencies much greater, or lower than 3000 Hz, the intensity of sound must be several orders of magnitude higher to be detected

    • This large range of intensities shows that the response of the ear is logarithmic

  • The decibel (dB) scale is also logarithmic 

    • Hence, the decibel scale is a useful way of measuring the response of the human ear to changes in sound intensity

The Decibel Scale

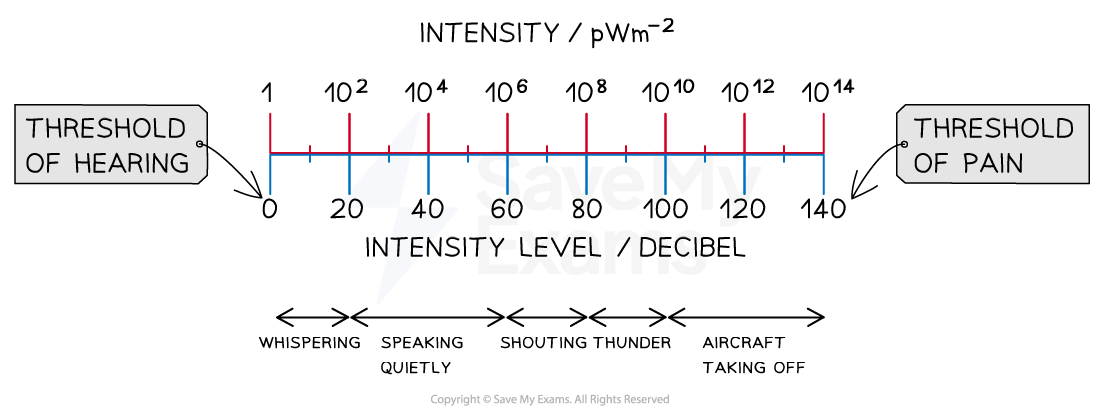
4s3YS9OO_10-2-2-the-decibel-scale

The decibel scale is used to represent the large range of intensities that the ear can detect on a logarithmic scale

Worked Example

Give two reasons why logarithmic scales are used to measure the loudness of a sound.

Answer:

  • The ear can detect sounds over a very large range of intensities, across many orders of magnitude

  • This means the ear’s perception of loudness is logarithmic

  • Therefore, a logarithmic scale is a useful way to plot or analyse such a large range of numbers

  • For example, on the graph above:

    • The range of frequency of human hearing is ~20 to 20 000 Hz

    • So, frequency values are plotted on the axes in increments of 10 (1, 10, 100, 1000, etc)

    • In this range of frequencies, intensity values range from 10−12 to 102 W m−2

    • So, intensity value are plotted on the axes in increments of 100 (10−12, 10−10, 10−8, 10−6, etc)

Loudness & Decibels

  • Intensity of a sound wave is defined as:

    The amount of sound energy that passes a point per second per unit area

  • Intensity can be described by the equation:

I space equals space P over A

  • Where

    • I = intensity of sound wave (W m−2)

    • P = power, or energy transferred per second (W)

    • A = area through which sound waves pass (m2)

  • For a sound wave that spreads out uniformly in all directions, it can be assumed to propagate as a spherical shell

    • The surface area of a sphere is 4 straight pi r squared

    • The radius r of this sphere is equal to the distance between the source of the sound and the receiver

  • This means the intensity of the sound spreads out according to an inverse square law

I space equals space fraction numerator P over denominator 4 straight pi r squared end fraction

Inverse Square Law of Sound Intensity

10-2-2-inverse-square-law-of-sound-intensity

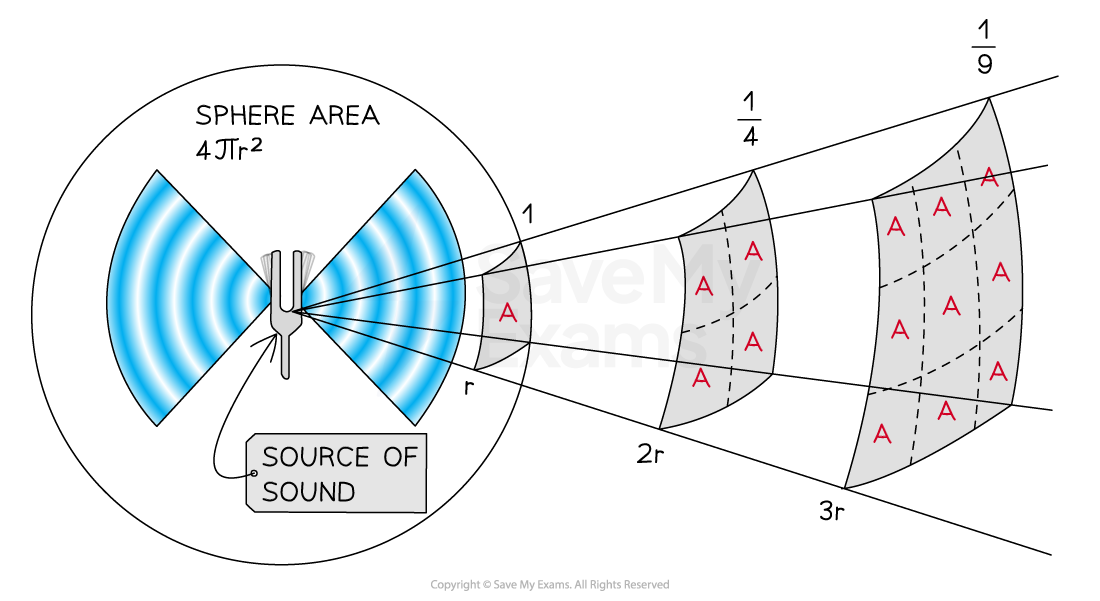
When the source of the sound is twice as far away, it has spread over four times the area, hence the intensity is four times smaller

  • The human ear can detect and respond to a very large range of intensities

  • The response of the ear to changes in sound intensity, or the perceived change in loudness, is directly proportional to the logarithm of the percentage change in intensity

perceived change in loudness proportional to space log space open parentheses I subscript 2 over I subscript 1 close parentheses

  • Where

    • I subscript 1 = initial intensity of sound wave (W m−2)

    • I subscript 2 = final intensity of sound wave (W m−2)

  • This is known as the logarithmic response of sound intensity

    • This means when the intensity of a sound doubles, and doubles again the loudness increases in fixed steps (for a given frequency)

    • For example, an increase in sound intensity from 1 × 10−12 W m−2 to 2 × 10−12 W m−2 is perceived to be the same change in loudness as 1 W m−2 to 2 W m−2

  • The threshold of hearing I subscript 0 is defined as:

    The lowest intensity that a normal human ear can detect at a frequency of 1 kHz

  • This is equal to about 1 × 10−12 W m−2

  • The intensity level of a sound can be defined as

intensity level = 10 log open parentheses I over I subscript 0 close parentheses

  • Where:

    • Intensity level is measured in decibels (dB)

    • I = intensity of the sound wave (W m−2)

    • I subscript 0 = threshold of hearing intensity = 1 × 10−12 W m−2

  • The threshold of hearing is assigned a sound level of 0 decibels, or 0 dB

    • An intensity level of 10 dB is 10 times louder than I subscript 0, or 1 × 10−11 W m−2

    • An intensity level of 20 dB is 100 times louder than I subscript 0, or 1 × 10−10 W m−2

    • An intensity level of 30 dB is 1000 times louder than I subscript 0, or 1 × 10−9 W m−2

Worked Example

Person A hears a sound of intensity level 95 dB. Person B hears the same sound at an intensity level of 82 dB whilst standing 20 m away from the source of the sound.

Calculate how far away person A is from the source of the sound.

Answer:

Step 1: Convert the intensity levels in dB into intensities

intensity level = 10 log open parentheses I over I subscript 0 close parentheses

  • Intensity level of person A = 10 log open parentheses I subscript A over I subscript 0 close parentheses = 95 dB

log space open parentheses I subscript A over I subscript 0 close parentheses space equals space 95 over 10 space equals space 9.5

  • Take logs of both sides:

I subscript A over I subscript 0 space equals space 10 to the power of 9.5 end exponent space space space rightwards double arrow space space space I subscript A space equals space I subscript 0 space cross times space 10 to the power of 9.5 end exponent

  • Intensity level of person B = 10 log open parentheses I subscript B over I subscript 0 close parentheses = 82 dB

log space open parentheses I subscript B over I subscript 0 close parentheses space equals space 82 over 10 space equals space 8.2

  • Take logs of both sides:

I subscript B over I subscript 0 space equals space 10 to the power of 8.2 end exponent space space space rightwards double arrow space space space I subscript B space equals space I subscript 0 space cross times space 10 to the power of 8.2 end exponent

Step 2: Use the inverse square law of intensity to find the ratio of IA and IB

  • Intensity of a sound wave:

I space equals space P over A space equals space fraction numerator P over denominator 4 straight pi r squared end fraction

  • Since the source of the sound is the same, the value of power P is the same, so I space proportional to space 1 over r squared

I subscript A over I subscript B space equals space open parentheses r subscript B over r subscript A close parentheses squared

Step 3: Rearrange and substitute values to find rA

r subscript B over r subscript A space equals space square root of I subscript A over I subscript B end root

r subscript A space equals space fraction numerator r subscript B over denominator square root of I subscript A over I subscript B end root end fraction space space space rightwards double arrow space space space r subscript A space equals space r subscript B space square root of I subscript B over I subscript A end root

r subscript A space equals space 20 space cross times space square root of 10 to the power of 8.2 end exponent over 10 to the power of 9.5 end exponent end root space equals space 4.5 space straight m

  • Hence, person A is standing 4.5 m from the source of the sound

Worked Example

On the ground near an airport, the intensity level of an aircraft taking off is measured to be 120 dB.

Determine the intensity level, in dB, due to two aircraft taking off at the same time.

Threshold of hearing, I subscript 0 space equals space 1.0 space cross times space 10 to the power of negative 12 end exponent space straight W space straight m to the power of negative 2 end exponent

Answer:

Step 1: Convert the intensity level in dB into intensity

intensity level (dB) = 10 log open parentheses I over I subscript 0 close parentheses

  • Intensity level due to each aircraft = 120 dB

10 space log space open parentheses I over I subscript 0 close parentheses space equals space 120 space space space space space rightwards double arrow space space space space space log space open parentheses I over I subscript 0 close parentheses space equals space 12

  • Take logs of both sides:

I over I subscript 0 space equals space 10 to the power of 12 space space space space space rightwards double arrow space space space space space I space equals space 10 to the power of 12 I subscript 0

  • Note: This is equivalent to I space equals space open parentheses 10 to the power of 12 close parentheses cross times open parentheses 1.0 cross times 10 to the power of negative 12 end exponent close parentheses space equals space 1.0 space straight W space straight m to the power of negative 2 end exponent, but it is simpler to keep in terms of I subscript 0 

Step 2: Add the intensities together to obtain the total intensity

  • Intensity due to both aircraft:

I space equals space 10 to the power of 12 I subscript 0 space plus thin space 10 to the power of 12 I subscript 0 space equals space 2 cross times 10 to the power of 12 I subscript 0

Step 3: Convert the intensity back into dB using the intensity level equation

intensity level (dB) = 10 space log space open parentheses fraction numerator 2 cross times 10 to the power of 12 I subscript 0 over denominator I subscript 0 end fraction close parentheses space equals space 10 space log space open parentheses 2 cross times 10 to the power of 12 close parentheses

intensity level due to both aircraft = 123 dB

Examiner Tips and Tricks

For two or more sounds, intensity levels in decibels cannot be added together to obtain a total intensity level, as this is not how logarithmic scales work. Remember to convert the values in decibels into intensities in W m−2, then you can add them together and convert back into decibels to obtain the intensity level of the combined sound waves.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Structure of the EarNext:Equal Loudness Curves
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.