Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesMedical PhysicsPhysics of the EyeLens Calculations

Lens Calculations (AQA A Level Physics)

Revision Note

Ann Howell

Last updated

Lens Calculations

Power

  • The power of a lens, P  is calculated using the following equation:

P = 1 over f

  • Where: 

    • P = power (dioptres, D)

    • f = focal length of the lens (m)

  • The focal length is measured from the centre of the lens

  • Power is inversely proportional to focal length

    • So the more powerful the lens the shorter the focal length

  • For a diverging (concave) lens, where the focal length is negative, power has a negative value

Worked Example

A diverging lens has a focal length of −1.5 cm.

Calculate the power of the lens.

Answer:

Step 1: Write the known values

  • Focal length, f = −1.5 cm

Step 2: Convert the focal length into m

  • 1 m = 100 cm

  • So, −1.5 cm = −1.5 ÷ 100 = −0.015 m

Step 3: Recall the equation for power and focal length

P space equals space 1 over f

Step 4: Substitute for focal length into the equation

P space equals space fraction numerator 1 over denominator negative 0.015 end fraction

Step 5: Calculate the power of the lens, P

P space equals space minus 66.6 D

Worked Example

A lens is set up between an object candle and a screen. All the equipment is arranged perpendicular to the desk. The image of the candle is in focus when the screen is positioned 60 cm from the lens.

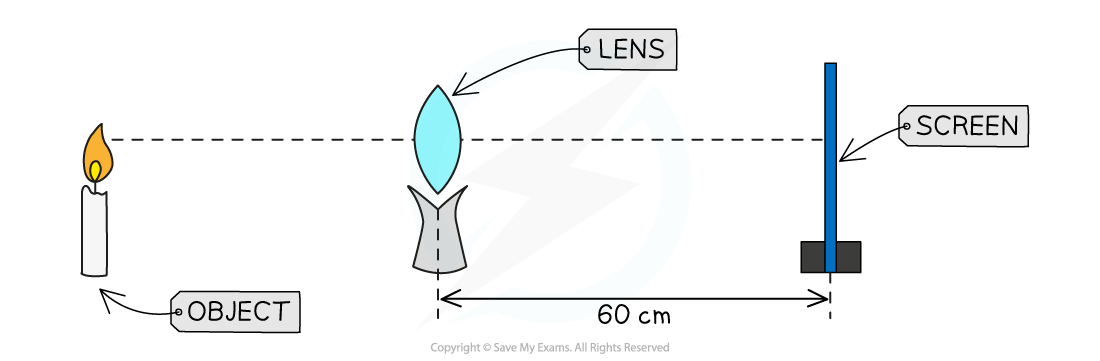
5-19-power-of-a-lens-we-qun_edexcel-al-physics-rn

Determine the power of the lens.

Answer:

Step 1: Write the known quantities in S.I. units

  • Image is in focus, so the screen is at the focal point

  • Focal length, f = 60 cm = 0.6 m

Step 2: Write the equation for power and substitute the values

P space equals space 1 over f space equals fraction numerator 1 over denominator 0.6 end fraction equals 1.67

Step 3: Give the full answer, to correct significant figures and with units

      The power of the lens, P = 1.7 D

Examiner Tips and Tricks

The explanations above relate to life in a common sense way. Stronger, more powerful reading glasses are used by people who have the weakest eye sight. They need lenses to do more of the focusing for them. 

The Lens Equation

  • This equation can be applied to all thin converging and diverging lenses

  • The equation relates the focal length of the lens to the distances from the lens to the image and the object

1 over f equals 1 over u plus 1 over v

  • Where:

    • f = focal length (m)

    • v = image distance from lens (m)

    • u = object distance from lens (m)

  • f, v and u do not all have to be in meters but they do have to be in the same units

    • They are measured from the centre of the lens

 

Labels of f, u and v on Converging and Diverging Ray Diagrams

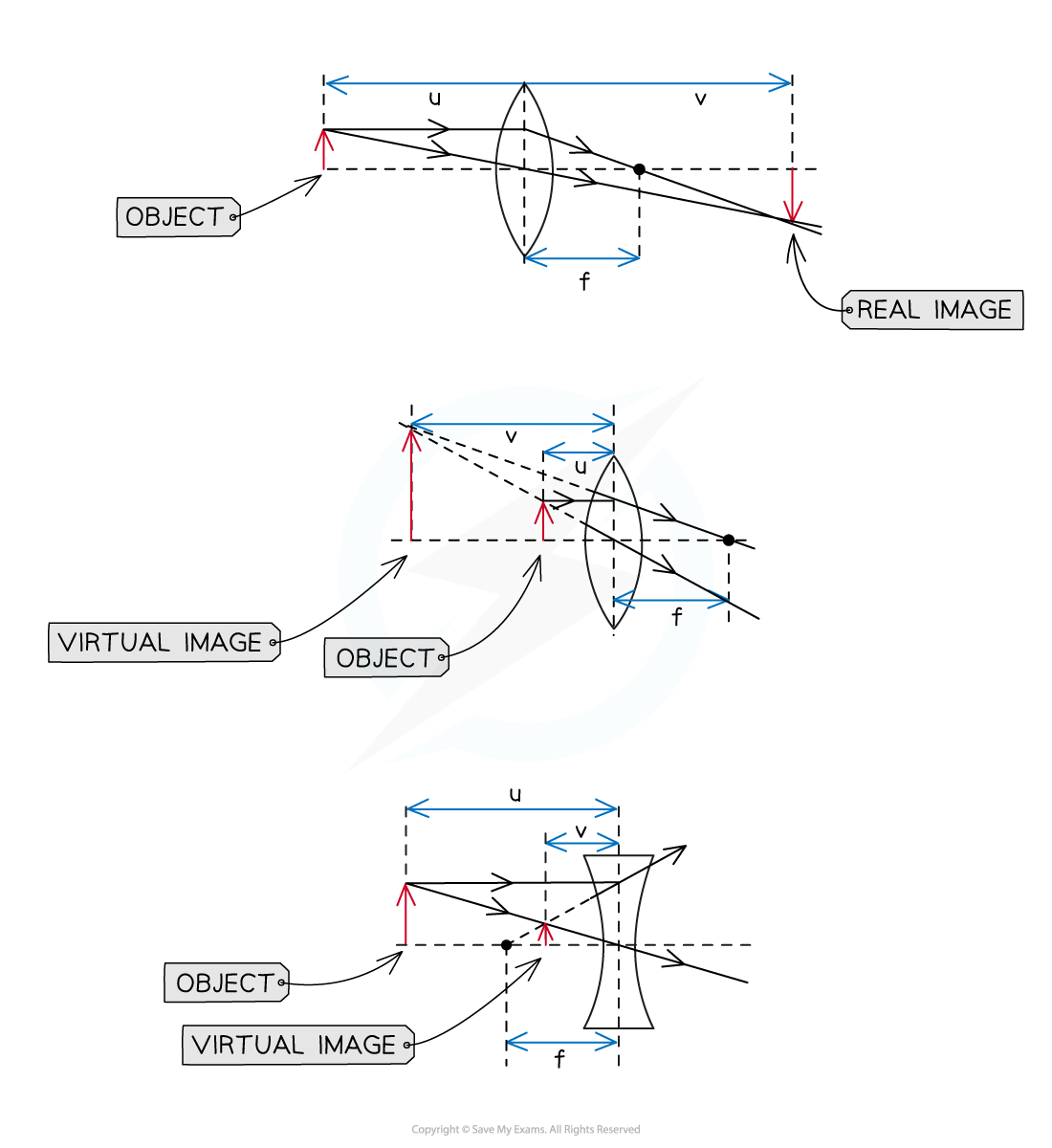
converging-and-diverging-lens-equation-diagram

Examples of where the lens equation can be used

 

  •  Remember that:

    • The values are positive if the image is real 

    • v is negative if the image is virtual 

    • f is negative if the lens is diverging

Worked Example

A student investigates the focal length of a thin lens by using it to project and image onto a screen.

The object is set 50.0 cm from the centre of the lens and the screen moved back and forth until the inverted image is sharp. This position is found to be 75.0 cm from the lens.

Determine the focal length of the lens.

Answer:

Step 1: Write the known values

  • Distance from object to lens, u = 50.0 cm

    • Distance from image to lens, v = 75.0 cm

Step 2: Write the equation and substitute in the values

1 over f equals 1 over u plus 1 over v space equals 1 over 50 plus 1 over 75 space equals 1 over 30

f = 30 cm

Examiner Tips and Tricks

It is easy to forget the last step in a calculation like this one. Remember that you are calculating 1 over f not f, and that you need to take the reciprocal of your answer.

Linear Magnification

Magnification as a Ratio of Heights

  • Magnification means how much larger the image is than the object

    • This is the ratio of the image/object height

m space equals h subscript i over h subscript o

  • Where:

    • m = magnification

    • hi = image height (m)

    • ho = object height (m)

Magnification as a Ratio of Distances

  • A diagram of an object and its real image will produce similar triangles

    • Therefore, the ratio of magnification is also represented by comparing the distance from the lens to the object and the image

 

Real Image Magnification as a Ratio of Image and Object Distances

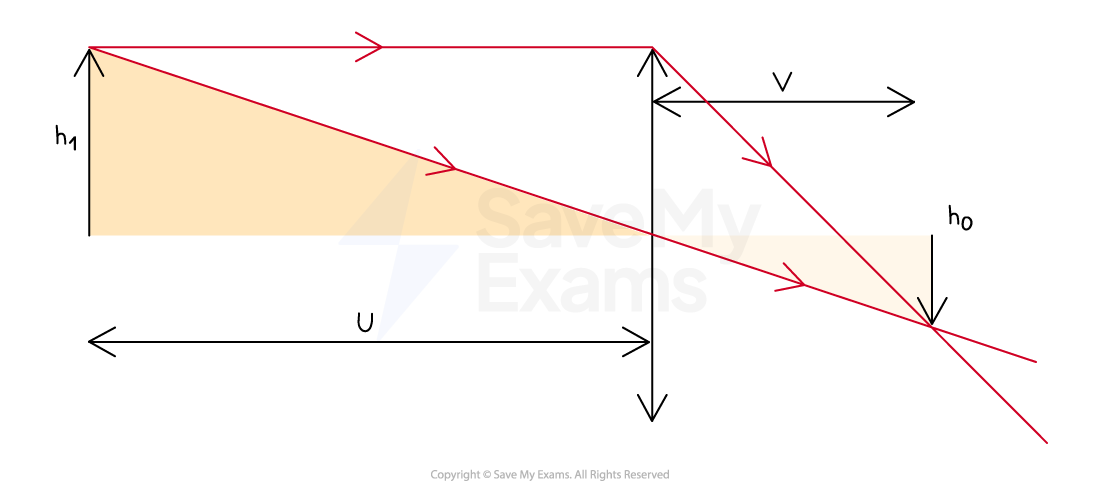
real-image-magnification-height-distance-derivation

The ratio of object distance u to image distance v is the same as object height h1 to image height h0 for a real image

  • This also works for virtual images

 

Virtual Image Magnification as a Ratio of Image and Object Distances

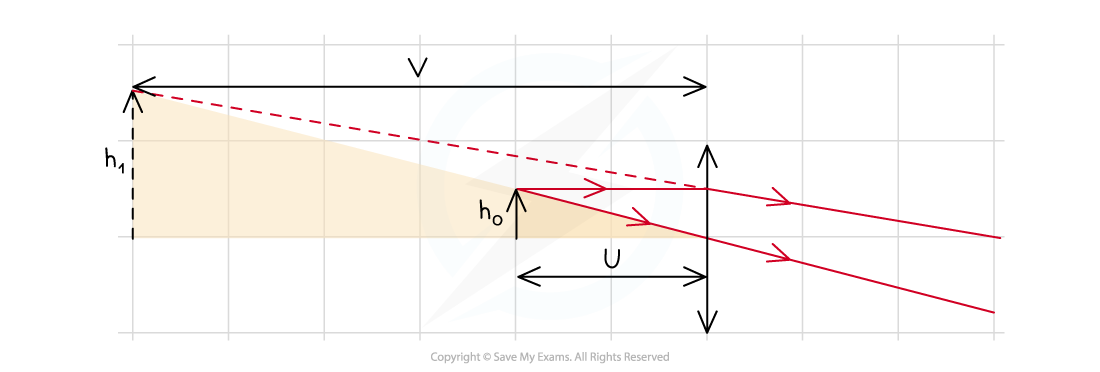
5-23-magnification-derivation-2_edexcel-al-physics-rn

The ratio of object distance u to image distance v is the same as object height h1 to image height h0 for a virtual image

 m space equals v over u

  • Where:

    • m = magnification

    • v = distance from lens to image (m)

    • u = distance from lens to object (m)

  • Since magnification is a ratio, it has no units

Worked Example

A magnifying glass has a focal length of 15 cm. It is held 5 cm away from a component which is being examined. 

Determine the magnification of the image.

Answer:

Step 1: Write the known values

  • Focal length, f = 15 cm

  • Distance between object and lens, u = 5 cm

Step 2: Use the lens formula and rearrange to make v the subject

1 over f equals 1 over u plus 1 over v

v equals open parentheses 1 over f minus 1 over u close parentheses to the power of negative 1 end exponent equals space open parentheses 1 over 15 minus 1 fifth close parentheses to the power of negative 1 end exponent space equals space minus space 7.5 space cm

  • The negative sign indicates a virtual image (expected for a magnifying glass) and is ignored for the next step

Step 3: Use the magnification formula to find the magnification of the image

m equals v over u space equals fraction numerator 7.5 over denominator space 5 end fraction space equals space 1.5

Worked Example

A person sees an image from a magnifying glass.

Magnification Worked Example Questions, downloadable IGCSE & GCSE Physics revision notes

Calculate the magnification of this image. Clearly show your working on the diagram.

Answer:

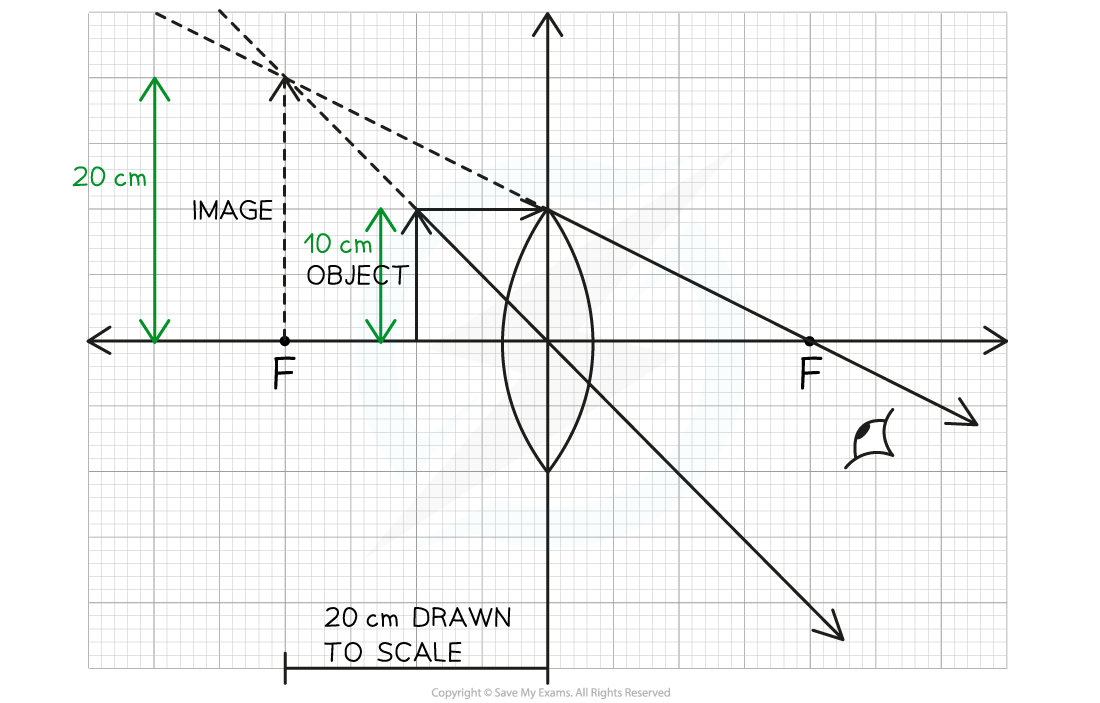
Magnification Worked Example Solution, downloadable IGCSE & GCSE Physics revision notes

Step 1: Measure the height of the object from the scale

The object is 10 cm

Step 2: Measure the height of image from the scale

The image is 20 cm

Step 3: Substitute values into the magnification equation

Magnification space equals space fraction numerator Image space height over denominator Object space height end fraction space equals space 20 over 10 space equals space 2

Examiner Tips and Tricks

The most common mistake with magnification calculations is to get the formula upside down.

Do a 'sanity check' by looking at the answer to make sure that magnified objects have got bigger (m > 1) and diminished ones smaller (m < 1).

Since we are working with ratios (so the units get cancelled out) this is one of those rare times when you don't need to convert everything to SI units, but do check that your units are all the same - for example all distances in cm.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Converging & Diverging LensesNext:Structure of the Eye
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.