The Normal Distribution (Edexcel A Level Maths): Revision Note
Exam code: 9MA0
Did this video help you?
Properties of a normal distribution
The binomial distribution is an example of a discrete probability distribution. The normal distribution is an example of a continuous probability distribution.
What is a continuous random variable?
A continuous random variable (often abbreviated to CRV) is a random variable that can take any value within a range of infinite values
Continuous random variables usually measure something
For example, height, weight, time, etc
What is a continuous probability distribution?
A continuous probability distribution is a probability distribution in which the random variable X is continuous
The probability of X being a particular value is always zero
P(X = k) = 0 for any value k
Instead we define the probability density function f(x) for a specific value
We talk about the probability of
being within a certain range
A continuous probability distribution can be represented by a continuous graph (the values for X along the horizontal axis and probability density on the vertical axis)
The area under the graph between the points x = a and x = b is equal to P(a ≤ X ≤ b)
The total area under the graph equals 1
As P(X = k) = 0 for any value
, it does not matter if we use strict or weak inequalities
P(X ≤ k) = P(X < k) for any value k
What is a normal distribution?
A normal distribution is a continuous probability distribution
The continuous random variable can follow a normal distribution if:
The distribution is symmetrical
The distribution is bell-shaped
If X follows a normal distribution then it is denoted
μ is the mean
σ2 is the variance
σ is the standard deviation
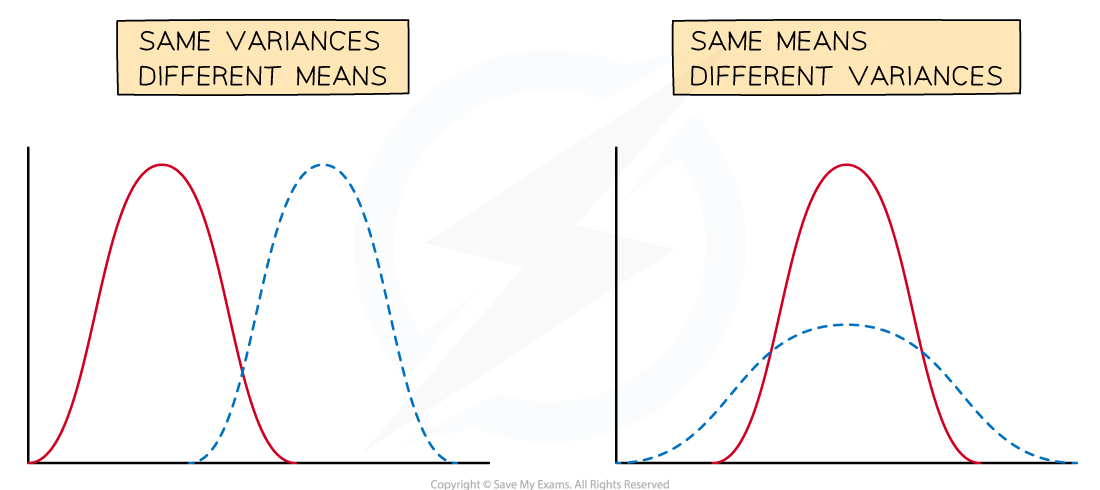
If the mean changes then the graph is translated horizontally
If the variance changes then the graph is stretched horizontally
A small variance leads to a tall curve with a narrow centre
A large variance leads to a short curve with a wide centre
What are the important properties of a normal distribution?
The mean is μ
The variance is σ2
If you need the standard deviation remember to square root this
The normal distribution is symmetrical about x = μ
Mean = Median = Mode = μ
The normal distribution curve has two points of inflection
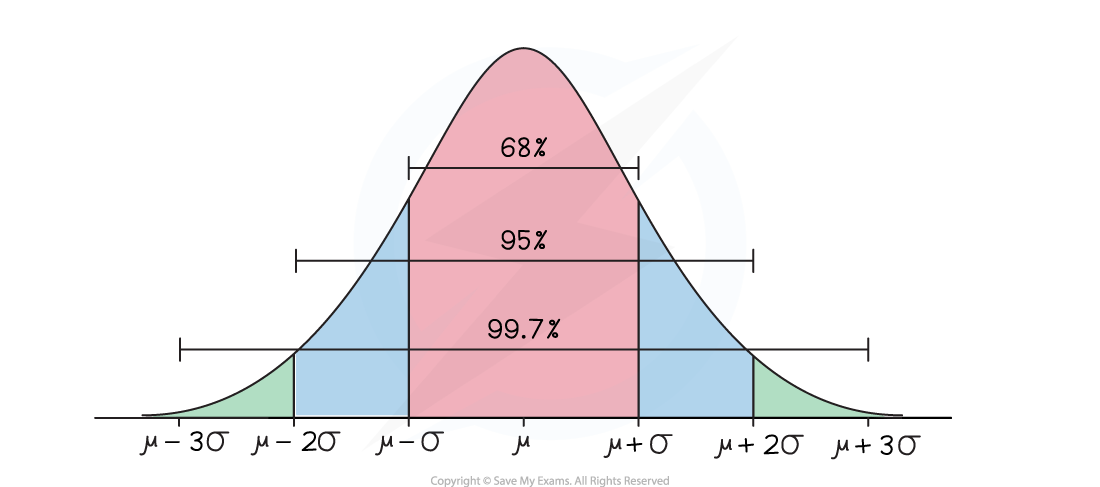
x = μ ± σ (one standard deviation away from the mean)
There are the results:
Approximately two-thirds (68%) of the data lies within one standard deviation of the mean (μ ± σ)
Approximately 95% of the data lies within two standard deviations of the mean (μ ± 2σ)
Nearly all of the data (99.7%) lies within three standard deviations of the mean (μ ± 3σ)
For any value x a z-score (or z-value) can be calculated which measures how many standard deviations x is away from the mean
Did this video help you?
Modelling with a normal distribution
What situations can be modelled by a normal distribution?
A lot of real-life continuous variables can be modelled by a normal distribution provided that the population is large enough and that the variable is symmetrical with one mode
For a normal distribution X can take any real value, however values far from the mean (more than 4 standard deviations away from the mean) have a probability density of practically zero
This fact allows us to model variables that are not defined for all real values such as height and weight
What situations can not be modelled by a normal distribution?
Variables which have more than one mode or no mode
For example, the number given by a random number generator
Variables which are not symmetrical
For example, how long a human lives for
Worked Example
The random variable S represents the speeds (mph) of a certain species of cheetahs when they run. The variable is modelled using N(40, 100).
(a) Write down the mean and standard deviation of the running speeds of cheetahs.
(b) State the two assumptions that have been made in order to use this model.
Answer:


Examiner Tips and Tricks
Remember the second number in N(x, y) is the variance, if you want the standard deviation then you need to square root it.

Unlock more, it's free!
Did this page help you?